Определение коэффициента самодиффузии воды в пакете Gromacs

Вода имеет ключевое значение во многих физических процессах, поэтому изучение ее свойств является важной научной задачей на протяжении многих лет. И хотя к настоящему времени по данной тематике проведено множество исследований [1,2], некоторые вопросы все еще остаются без ответа [3]. В частности, до сих пор не закончено изучение структурных свойств воды в критической области, поэтому эта область не затрагивается во многих обзорах [4]. Целью настоящей работы является определение границ применимости потенциала SPC при моделировании поведения воды в широком температурном диапазоне критических состояний в пакете Gro macs (рис. 1). Исследуемая область выбрана с учетом возможного применения в технике, например, паросиловых установках и ВВЭР (Водо- £ водяной энергетический реактор). | Gromacs - многофункциональный па- § кет, использующий метод молекуляр- 5 ной динамики для систем, состоящих из большого числа частиц, в состав которого входит большая база полу-эмпирических парных межчастичных потенциалов для наиболее часто используемых веществ.

Температура. К

Рис. 1. Фазовая диаграмма воды, жирной линией отмечена исследуемая область

В работе проведено моделирование системы, состоящей из 216 моле- кул воды с использованием трехточечного потенциала, называемого в текущей литературе SPC [5], с периодическими граничными условиями. Модельный SPC-потенциал представляет молекулу воды в виде трех точечных зарядов: двух с зарядом qx = 0,41е (атомы водорода) и одного с 72 = “0,81е (атом кислорода), для которого кроме электростатического потенциала добавлен потенциал типа Леннарда-Джонса (сг= 3,016 А, энергия е- 15,319 кДж/моль). Приближенный характер SPC-потенциала несколько искажает равновесные параметры одиночной молекулы. В молекуле воды угол между О—Н связями и их длина составляют соответственно 6 = 104,52° и /1 = 0,9584 А против 6 = 109,47° и / = 1 Ав модели SPC.

Рис. 2. Схема модели воды потенциала SPC

Стартовая конфигурация для моделирования задавалась следующим образом: координаты атомов были равномерно распре- делены по кубической ячейке, а их начальные скорости инициализировались с помощью встроенного в пакет генератора случайных чисел, и удовлетворяли распределению Максвелла. Временной шаг моделирования был выбран равным 0,002 пс [6], а так как число шагов 20 000, то полное время моделирования составило 40 пс [7]. Тестовые прогоны показали, что для установления равновесия требуется не более 2 пс. Для моделирования системы в NPT-ансамбле использовались термостат и баростат Берендсена [8], обеспечивающие сходимость температуры и давления системы к установленным значениям То и Ро в соответствии с динамическими уравнениями:

ат _т0-т ар _р0-р at т ’ at тр где тР, т - константы времени, являющиеся входными параметрами программы моделирования.

Моделирование проводилось при постоянном давлении и температуре (в т. н. NPT-ансамбле), в диапазоне изменений давления Р от 500 бар до 3000 бар и температуры Т от 300 К до 700 К. Число молекул N сохранялось постоянным и равным 216, что как показано в работе [9] является достаточным для получения результатов с погрешностью не хуже 5 %. Дополнительные моделирования с 820 молекулами подтвердили, что погрешность действительно лежит в этих пределах. По усредненным данным определялись величины объема, давления и температуры, а также парная корреляционная функция g(r). Отклонение средних величин давления и температуры от заданных баростатом и термостатом лежит в пределах 6 %. Коэффициент самодиффузии вычислялся по формуле л (Аг²)           2_Х

D =----- , где (Аг ) - средний квадрат

6т полного смещения молекулы воды за время т . Использовался метод наименьших квадратов при его определении. Полученные при моделировании результаты сопоставлялись с экспериментальными данными работ [7, 10].

Сравнение результатов моделирования температурной зависимости коэффициента самодиффузии D воды с данными эксперимента (рис. 3) показало, что в области

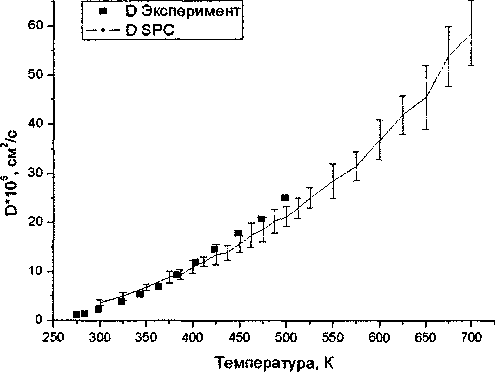
Рис. 3. Сравнение результатов моделирования температурной зависимости коэффициента самодиффузии воды с данными эксперимента [10] при Р = 1000 бар

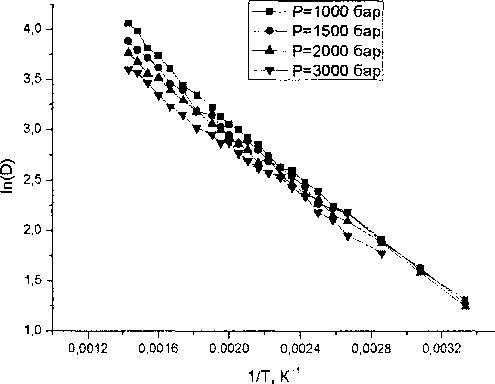
Рис. 4. Температурные зависимость коэффициента диффузии воды в координатах

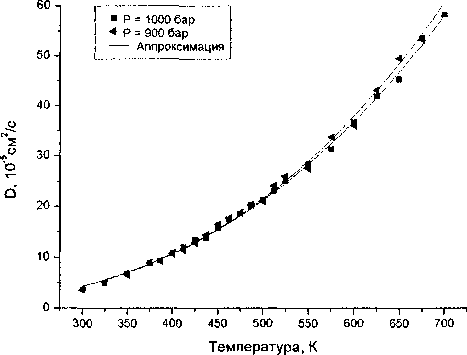
Рис. 5. Аппроксимация температурной зависимости коэффициента диффузии

Физика

температур 300-450 К расхождение находится в пределах расчетной погрешности, однако в об

ласти более высоких температур моделирование несколько занижает величину D.

Существует альтернативный безакти-вационный подход к рассмотрению процессов диффузии в жидкости. Для многих из них зависимость коэффициента само-диффузии D в широком диапазоне температур описывается уравнением Арре

0,45 ч

0,40 -

0,35-

ниуса, которое при учете приложенного

давления,

D-Dq exp

имеет          вид

—- [HL где D_o

постоянная слабо зависящая от температуры, E_d - молярная энергия активации, 7? - универсальная газовая постоянная, V_D - так называемый активационный объем. Зависимость 1п(£>) при высоком давлении, как видно из рис. 4, ведет себя

0,30-

0,25 -

0,20 -

0,15-

■ —Т=700 К

• -Т=600 К

▼- Т=500 К

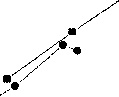
Молярный объем, см3/моль

Рис. 6. Зависимость ОТ”0,763 от молярного объема, построенная по данным МД-моделирования

прямо пропорционально \(Т в диапазоне от 300 К до 700 К. Это позволяет нам выделить актива

ционные параметры:

^DP ~

dln(D)

Sln(l/r)Jp

R и V_d=-RT

dln(Z>)

ЭР

. Результаты расчета указан

ных величин приведены в табл. 1. Для сравнения там же приведены определенные экспериментально значения энергии активации при постоянном объеме E_dv , которые определяются аналогично и согласно [10] слабо отличаются от величин E_DP . Результаты сравнения показывают, что найденные при моделировании энергии активации находятся в неплохом согласии с данными эксперимента. При увеличении температуры, при постоянной плотности, энергия активации убывает, а при увеличении плотности, при постоянной температуре, - увеличивается. Расхождение значений энергии активации при моделировании и эксперименте, не выходит за границы допустимой погрешности, и возникает в первую очередь из-за отличий в определении E_DP и E_dv . Активационный объем V_D меняется следующим образом: при 7=700 К - от 9,6 см³/моль при 2,5 кбар до 33,7 см³/моль при 0,95 кбар, при Т= 600 К - от 6,2 см³/моль при 2,5 кбар до 14,8 см³/моль при 0,95 кбар, что согласуется с экспериментальными данными[10].

Таблица 1

Сравнение расчетных и экспериментальных значений энергии активации

Моделирование			Эксперимент
р, кг/м3	Т,К	Edp , кДж/моль	р, кг/м3	Т , К	Edv , кДж/моль
928	425	11,5	940	423	12,2
964	387	10,7	9,6	383	14,3
955	425	11,9	940	423	12,2
987	387	11,7	980	383	13,6
1016	350	11,4	1020	343	14,1
977	425	10,6	980	423	7,9
1007	387	10,1	1000	383	11,8

Существует еще одна точка зрения на природу диффузии, согласно которой основную роль играют не активационные процессы, а случайное перераспределение свободного пространства внутри жидкости [13]. При такой трактовке зависимость коэффициента диффузии от температу ры и давления имеет вид [10, 13]

В(Р) ' T-W))

D = А(Р^² ехр

Булдашев И.В., Мирзоев А.А.

Как видно из рис. 5, указанная зависимость также прекрасно описывает температурное поведение коэффициента диффузии воды в исследуемом диапазоне состояний, как и уравнение Аррениуса. Получаемые при такой подгонке значения коэффициентов А, В, Т_о приведены в табл. 2 для ряда значений давления.

Отметим также, что в работе [13] была теоретически выведена и подтверждена экспериментально зависимость D ос TⁿV_m , где V_m - молярный объем вдоль изотерм в сверхкритической области. Полученные нами результаты моделирования подтверждают указанную зависимость при значении и = 0,763 в диапазоне температур 500-700 К (рис. 6).

Таблица 2

Зависимость коэффициентов А,В,Т_У от давления

Давление, кбар	0,8	0,9	1,0	1,5	3
А	2273,3	147,9	94,0	27,0	9,8
В	11196,7	4833,0	4125,3	2487,8	1618,7
То	-947,0	-460,7	-398,5	-227,6	-130,4

Таким образом, проведенное нами моделирование самодиффузии в широком температурном диапазоне вдоль нескольких изобар в сверхкритической области состояний, позволяет сделать следующие выводы:

• а)    потенциал SPC позволяет получать количественно точные значения коэффициента диффузии воды в диапазоне 300-500 К, однако в области более высоких температур приводит к заниженным оценкам указанной величины;

• б)    температурная зависимость коэффициента самодиффузии воды при различных значениях давления одинаково хорошо аппроксимируется как кривыми типа Аррениуса, так и уравнением Коэна-Турнбулла [13];

• в)    показано, что предложенная в работе [10] эмпирическая зависимость коэффициента самодиффузии DccTⁿy_m, где V_m - молярный объем, при значении п = 0,763 вдоль изотерм в сверхкритической области, выполняется и в исследованном нами диапазоне температур 500-700 К.