Определение коэффициентов диффузии экстрактивных веществ в люпине

Скорость процесса экстрагирования из люпина - сырья растительного происхождения с капиллярной структурой - определяется скоростью молекулярной диффузии (или просто диффузии) целевого компонента. Предполагается, что процесс не осложнён химическим взаимодействием на границе раздела фаз. При диффузии вещество переходит из одной части системы в другую вследствие беспорядочных движений атомов и молекул [1].

Согласно первому закону Фика [2] в изотропной среде количество диффундирующего вещества j, переходящее в единицу времени через единицу площади поперечного сечения, пропорционально градиенту концентрации, измеряемому по нормали к этому сечению:

j = - DgradC ,            (1)

где D - коэффициент диффузии; C - концентрация диффундирующего вещества.

Следствием закона Фика является дифференциальное уравнение диффузии:

д С- п ⁵² с

=         , дт     дx2

где т - время, x - координата.

Запишем уравнение для расчёта концентраций (распределение целевого понента в объёме частицы) [3, 5]:

д с J д2 с д2 с д2 с) = D ++ дт     ^дx2 ду2 дz2у

поля ком-

Это уравнение можно переписать иначе:

д с J д ² с г д с )

-= D —- +--- дт ^д ^ ² ^ дс _у

где ^ - постоянная координата, которая для пла стины равна х, для шара и цилиндра равно r; r - расстояние от оси; Г - постоянная, величина которой зависит от геометрической формы частиц (для частиц плоской формы (пластины) Г = 0, для протяжённых частиц цилиндрической формы Г = 1, и для шара Г = 2 [1, 6].

С целью получения исчерпывающей физической информации о процессе дополним уравнение (3) условиями однозначности.

Начальное условие:

с ( x , у , z ,0) = с о , (5)

или

Ц ( x , у , z ,0) = Ц о , (6) где с ₀ - начальная концентрация компонента в порах; ц - вязкость жидкости в капиллярах; ц ₀ - химический потенциал, соответствующий концентрации с ₀ .

Начальное условие (5) представляет собой известное распределение концентрации в исследуемом объёме в начальный момент времени.

Сформулируем граничное условие третьего рода для уравнения (4). В нашем случае рассматривается задача о распределении концентрации в твёрдом теле и в этом теле имеет место диффузионный массоперенос. При этом экстрагент с присутствием в нём целевого компонента обтекает наружную поверхность тела [9]. Тогда граничное условие третьего рода имеет вид:

- D m 1^1 = р (с п - Q, (7)

<д n J п где DM - коэффициент массопроводности; n - расстояние по нормали к поверхности пористой частицы; в - коэффициент массоот-дачи; с 1 - концентрация целевого компонента во внешней среде; индекс «П» означает поверхность.

Используя дифференциальное уравнение молекулярной диффузии (4) при краевых условиях (5) и (7), можно установить распределение концентраций по объёму тела во времени [2]. Для упрощения решения предлагается использовать изменение среднего значения с по объёму тела.

Тогда обобщённое теоретическое решение для шара, неограниченной пластины и неограниченного цилиндра запишется в виде:

с - с ”      4( v + 1) • Bi m       - ц 2 D т R 2

с 0 - Q   ^ ц ²( Bi n - 2 v • Bi m + ц . e ’^

где v = +1/2 для шара; v = -1/2 для неограниченной пластины; v = 0 для неограниченного цилиндра; Bim - массообмен-ный (диффузион ный) критерий Био - соотношение между внутренним и внешним диффузионными сопротивлениями, Bim = в^ R / Dm ; R - определяющий размер (для шара и неограниченного цилиндра - радиус, для неограниченной пластины -половина толщины пластины); цп - корни ха рактеристического уравнения.

Используя [7], находим:

ц ^{ctg Ц} = Bi m

J v + 1 ( Ц ) = Bi m J v ( Ц )      Ц ,

где J _{v + 1} и J _v - функции Бесселя, индекс которых равен целому числу плюс 1/2, выражаются через тригонометрические функции.

ВестникВГУИТ, №2, 2014

Основываясь на [1, 2], запишем:

J - у( ц ) = з — cos ц ; J u( ц ) = _л 2 sin ц ;

⁷² \лц ⁷²      \ лц

, .     2 fsinцI

J з/( ц) =—I--cos ц|.(10)

2 \лцу цJ

Корни характеристических уравнений ц _п и коэффициенты при экспонентах Bn в (7) в зависимости от критерия Bi_m приведены в [2].

Поток растворённого вещества j с поверхности F полуограниченного тела является первостепенной характеристикой процесса. А.В. Лыков получил следующее решение при такой постановке задачи:

j = в • F -A Ce^y • erfcy ,        (11)

B ₁ = -6 2 , ц = n - для     шара;      B ₁ = 0,69,

n ц1 = 2,4 - для неограниченного цилиндра.

Прологарифмировав уравнение (13) [10]:

или

или

ln

^{f с} - C 1 J

< C 0

ln

—

C 1 J

C - C,

С -С

V C 0 C 1 7

ln

- ц DT/ ln B ₁ + In e " /R ²,

= ln B ₁

-

2 DT _л ц —^In e .

1 R 2

где A C = C _o - C ; у = в ------( в - коэффи-

^{0   1}          m p D M

^f с - с,_ 'I V C 0 - C 1 J

= In B ₁

- 0,998 ц 1 ² -у.

R

циент массоотдачи, m p - пористость полуогра-

2 7 _У ²

ниченного тела); erfcy = 1 —;= f e ^y V П у

С целью определения коэффициента молекулярной диффузии перепишем уравнение (16):

• dy - табу-

ln

лированная функция [4].

Уравнение (11) упрощается в случае интенсивной массоотдачи, либо в случае длительного промежутка времени. Путём предельного перехода (2) при у ^ да из (11) вытекает:

^f c-c,_ ¹ V C 0 - C 1 J

- ln B ₁

= |- 0,998 ц ² -2-1 V R J

Уравнение (17) после подстановки вместо констант B ₁ и ц ₁ из значений для неограниченной пластины имеет вид:

mD j = FAC.  p M (12)

N пт

Привлекательность уравнений (11) и (12) заключается в том, что они пригодны для расчёта массового потока целевых компон ентов из капилляра с известной площадью поверхности F . Значение пористости полуограничен-ного тела в этом случае m p = 1.

На основании вышеизложенного можно

In

^{f C} - C 1 '

V ^C 0

-

-

C 1 J

1 I 8

I

V п

|₂0,998 ц 12

V

•

D T ]• (¹⁸)

Разделив левую и правую части равенства (18) на (-1) и используя основное свойство

пропорции, получим основное выражение для

расчёта коэффициента диффузии:

D =

или

получить кинетическую кривую процесса:

C - C.

In------ ^L = f ( т ).

r

C ₀ C ₁

Ограничиваются в уравнении (7) первым её членом, поскольку определённая доля извлечённого компонента соответствует моменту

времени т ₁ :

C - C 1

= B 1 ^e

C ₀ C ₁

ц п DV

R ²

.

Здесь B1 и ц - константы. Когда Bim = да, то B1 и ц принимает значения: В1 = —^, п

к ц = — - для

неограниченной пластины;

4 R ²

0,998 • n ² - т

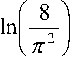
+ In f CZCL ' V C 0 - C1 J

D = 4,01 R² n ² • т

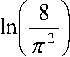
+ In f C-cl J. V C 0 - C1 J

Таким образом, уравнение (20) позволя-

ет рассчитать коэффициент диффузии формы тела – неограниченная пластина.

Аналогично получено уравнение определения D (форма тела – шар ) [20]:

D =

R ²

0,998 n ² • т

= ln f -^2 J + In

^{f C} - C 1 J

V ^C 0

-

C ₁ J_J

.

Нами выписано также уравнение

для

для

для

расчёта коэффициента диффузии D (форма тела – неограниченный цилиндр ):

D =-----------= ln ( 0,69 ) + In

0,998 • 2,4 • т ^v ’

^{f C} - C 1 J

r V ^C 0

-

C ₁ J_J

.

По приведённым уравнениям (20), (21) были рассчитаны коэффициенты диффузии при экстрагировании целевых компонентов жидким диоксидом углерода из зёрен ячменя, плодов жёлудя и корней цикория, измельчённых в крупку (форма тела - шар) и в лепесток (форма тела - неограниченная пластина). Результаты приведены в [10].

Интуиция подсказывает, что приведённые соотношения (20), (21), (22) будут справедливы и для других видов сырья растительного происхождения с капиллярно-пористой структурой, поскольку базовое уравнение (13) является неизменным.

Далее представлены данные об изменении коэффициентов диффузии экстрактивных веществ в люпине при экстрагировании подсырной сывороткой, проведен анализ результатов.

Молекулярный коэффициент диффузии зависит от структуры твёрдого тела, температуры и растворимых веществ. В то же время он не зависит от гидродинамических условий на поверхности твёрдых частиц, а также конструкции аппарата.

Полагая, что структура твёрдого тела не изменяется, проанализируем изменение коэффициента диффузии от времени в растительном сырье, используя с этой целью экспериментальный материал по кинетике процесса экстрагирования [6].

При количественной интерпретации исходили из следующих предпосылок [2, 8].

• 1.    Тела растительного происхождения обладают характерным клеточным строением, которое может быть нарушено механическими взаимодействиями. Строение пор во многом определяет механизм извлечения и скорость его протекания. Размеры частиц люпина значительно превышают диаметры пор, поэтому их можно рассматривать как изотропные пористые тела.

• 2.    После механической обработки частицы люпина имели форму шара, цилиндра и пластины. Диаметр цилиндра d ср значительно меньше его длины ( l / d ср = 10), а толщина 5 плacтины меньше ширины b и длины l ( b / 5 = 5, b / 5 = 10). Известно, что если один из рaзмеров превышaeт кaждый из остaʙшихся в 4 и более раз, то такие тела можно рассматривать как неограниченные. В них устанавливается одномерный диффузионный поток ʙ направлении минимального размера.

• 3.    Экстрактивные вещества - это группа компонентов с рaзличными диффузионными и физико-химическими свойствами. В нашем случае совокупность всех экстрактивных веществ дифференцируется, поскольку целевым продуктом является белок люпина.

• 4.    В сырье растительного происхождения, представителем которого является и люпин, часть целевых компонентов находится в области застоя, то есть в труднодоступных для экстрагента зонах или замкнутых порах [2]. Тогда следует исключить эту часть их кинетических расчётов.

С учётом изложенных предпосылок записаны уравнения (13-22) для неограниченных форм люпина в виде логарифмических уравнений нестационарной диффузии. Результаты расчётов приведены в графической интерпретации (рисунки 1, 2).

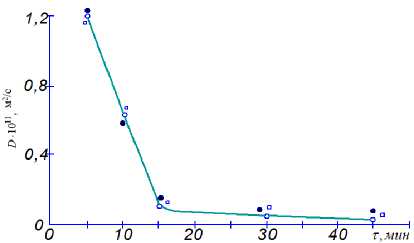
Рисунок 1. Изменение коэффициентов диффузии экстрактивных веществ в люпине в процессе экстрагирования (обобщённая кривая): о - пластина,* - цилиндр, = - крупка.

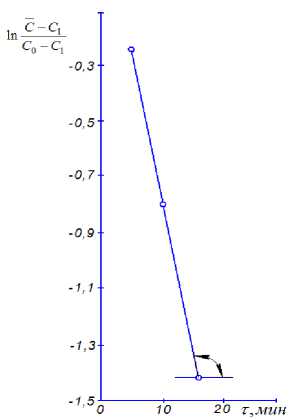
Рисунок 2. Зависимость концентрации экстрактивных веществ в люпине от продолжительности процесса (регулярный режим).

Как видно из рисунка 1, коэффициент диффузии D не зaʙисит от геометрической формы люпина, поскольку кривые располагаются близко друг к другу. Это позволило получить одну обобщённую зависимость D( т ) для крупки, цилиндра и пластины. Коэффициент D имеет максимальное значение по истечении 300 с экстрагирования, а затем резко снижается. Значение D после 900 с практически не изменяется (кривая располагается вблизи оси абсцисс).

Уравнение (17) позволило нам определить коэффициент диффузии, используя экспериментальные данные (рисунок 2). Угловой коэффициент прямой µ ₁ ² ⋅ D /( δ /2) ² составил 2,1·10^-4 с^-1. Учитывая приведённые ранее значения µ и δ , был найден коэффициент диффузии D = 2,1·10^-11 м²/с.

Таким образом, получено одно значение D для прямой, являющейся областью регу- лярного режима. Сопоставление графических изображений (рисунки 1 и 2) позволяет заключить, что результаты находятся в удовлетворительном согласии.