Определение коэффициентов энергетической связи балок, соединенных под углом
Автор: Кравчуновский А. П.
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Информатика, вычислительная техника и управление
Статья в выпуске: 1 т.25, 2024 года.
Бесплатный доступ
Использование статистического энергетического метода для анализа динамических систем предполагает, что коэффициенты энергетической связи подсистем должны быть известны. Коэффициенты энергетической связи показывают, какая часть энергии переходит из одной подсистемы в другую. Они входят в систему уравнений энергетического баланса и предварительно должны быть определены аналитически, экспериментально или численно. Наиболее перспективным из перечисленных методов является численный. В частности, в данной статье использован метод конечных элементов. Целью настоящего исследования является определение коэффициентов энергетической связи двух подсистем в двух вариантах их относительного положения. За основу принята модель Г-образного соединения двух балок, которая довольно часто встречается в подобных исследованиях. Г-образное соединение частей конструкции часто встречается в строительных сооружениях, однако в других отраслях, таких как разработка космической и авиационной техники, зачастую элементы конструкции соединяются под углом, отличным от прямого. А поскольку энергетические методы могут применяться и для аэрокосмической отрасли, при разработке подходов к анализу конструкций с помощью таких методов будет полезным знание о том, как меняются энергетические параметры системы, в частности коэффициенты энергетической связи, в зависимости от того, под каким углом выполнено сопряжение их составных частей. Рассмотрены две конфигурации системы: в первой - балки соединены под прямым углом, во второй - под углом 45°. Вычислены коэффициенты энергетической связи балок для обеих конфигураций системы. Сделаны выводы о возможности распространения полученного результата на более сложные конструкции, а именно конструкции космической техники.
Энергетический метод, коэффициент энергетической связи, уравнение энергетического баланса, космический аппарат, колебания
Короткий адрес: https://sciup.org/148328309
IDR: 148328309 | УДК: 534.1 | DOI: 10.31772/2712-8970-2024-25-1-18-24
Текст научной статьи Определение коэффициентов энергетической связи балок, соединенных под углом
В современной практике для анализа сложных конструкций наравне с широко известным методом конечных элементов (МКЭ) также используются и чуть менее распространенный статистический энергетический метод (СЭМ) или как чаще его можно встретить в зарубежной литературе SEA – Statistical Energy Analysis. Статистический – поскольку предполагается, что исследуемые системы принадлежат статистическим совокупностям с известным распределением динамических параметров [1–4].
Анализ системы с помощью СЭМ, как и с помощью МКЭ, предполагает разбиение системы на более простые подсистемы. Однако СЭМ допускает значительно более крупное разбиение, что экономит временные и вычислительные ресурсы, т. е. достаточно получить такую составную единицу системы, чтобы в ней распространялись колебательные волны одного типа. В то время, как для анализа сложной системы с помощью МКЭ (особенно на высоких частотах), требуется сильно уменьшать размер конечного элемента, и тем самым увеличивать размерность всей системы с целью получения достоверного результата [5].
В основу СЭМ положен закон сохранения энергии, согласно которому полная энергия замкнутой системы сохраняется [6]. Для решения составляется баланс энергий, вводимых в систему и поглощенных ею, а также переходящих из одной подсистемы в другую [7].
Процесс перетекания энергии между подсистемами математически описывается так называемыми коэффициентами энергетической связи подсистем. Они могут быть найдены аналитически, экспериментально или численно. Аналитические зависимости далеко не всегда применимы в силу сложности моделируемых реальных конструкций, экспериментальные – зачастую слишком трудоемки. Наиболее перспективными для этих целей являются численные методы.
Постановка задачи
В СЭМ система разделяется на несколько связанных подсистем, объединяющих моды одного типа (изгибные, крутильные или продольные). Метод является статистическим в том смысле, что рассматриваемые подсистемы условно должны объединять группы идентичных объектов, которые должны обладать аналогичными динамическими свойствами [1]. Метод основан на вычислении энергии, передающейся от одной подсистемы к другой. Энергия каждой подсистемы может рассеиваться посредством демпфирования, которое выражается величиной коэффициента потерь, или переходить в смежные подсистемы [8]. Коэффициент энергетической связи показывает, какая часть энергии переходит из одной подсистемы в другую. Таким образом, переменной в анализе выступа- ет энергия. Предполагается, что энергия сконцентрирована только на резонансных модах. При этом полная энергия каждой подсистемы представляет собой сумму энергий каждой моды.
Основу СЭМ составляет система уравнений энергетического баланса (СУЭБ), которая имеет вид
n
П1+ ЕП1 i -П21 -Пи i=2
n
-
-П 12 П 2 + ^Ъ i -П 32
i = 1
i # 2
n
-
-П 13 -П 23 П з + ^ П з i
i = 1
i # 3
-n n 1
-n n 2
-n n 3
■ П 1 n
-П 2 n -П 3 n
n
П n +£П ni i =1
i # n
E 1
E 2
E 3
E n
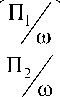
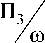
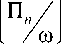
Здесь η i – коэффициенты внутренних потерь подсистем; η ij – коэффициенты энергетической связи подсистем; E i – колебательные энергии подсистем; П i – мощности, вводимые в подсистемы; ω – круговая частота; n – количество подсистем.
Правая часть СУЭБ определяет вводимые в подсистемы энергии, в то время как левая часть определяет колебательные энергии системы. Количество уравнений, входящих в СУЭБ, должно быть равно количеству подсистем. В вектор-столбце правой части СУЭБ не равны нулю только компоненты тех подсистем, в которые вводится энергия.
Колебательная энергия, используемая в расчете, – полная механическая энергия, которая представляет собой сумму кинетической и потенциальной энергий каждой подсистемы и является неизвестной в уравнениях. Предполагается, что вводимые мощности предварительно вычислены, а коэффициенты потерь и коэффициенты связи подсистем приняты по аналогии с уже проведенными расчетами идентичных конструкций и известны при составлении СУЭБ.
Как было отмечено выше, аналитические и экспериментальные способы определения коэффициентов энергетической связи не являются универсальными, и предпочтение в данном случае следует отдать численным методам. Использование для этих целей МКЭ является перспективным и удобным подходом [9–13].
Так, в статье [14] рассмотрено Г-образное соединение двух балок, на примере которого с помощью МКЭ были найдены коэффициенты энергетической связи при переходе энергии из первой балки во вторую.
Г-образное соединение частей конструкции действительно часто встречается в строительных сооружениях, однако в других отраслях, таких как разработка космической и авиационной техники, зачастую элементы конструкции соединяются под углом, отличным от прямого. А поскольку ЭМ может применяться и для аэрокосмической отрасли, при разработке подходов к анализу конструкций с помощью ЭМ будет полезным знание о том, как меняются энергетические параметры системы, в частности коэффициенты энергетической связи, в зависимости от того, под каким углом выполнено сопряжение их составных частей.
Так, например, ячейка сетчатой изогридной (или анизогридной) структуры силовой конструкции космического аппарата подразумевает соединение ребер под произвольными углами.
В настоящем исследовании для контроля расчетных параметров возьмем за основу балочную модель из статьи [14], но изменим некоторые условия под задачи анализа.
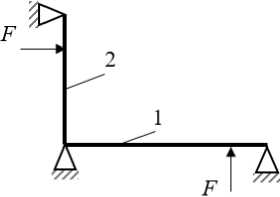
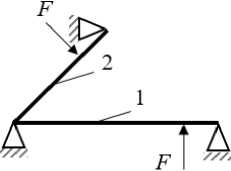
Рассмотрим систему, представленную двумя шарнирно опертыми балками, жестко соединенными между собой (рис. 1). Для удобства исследования граничные условия выбраны таким обра- зом, чтобы в балках возникали только изгибные колебания. Длина первой балки 1,1 м, длина второй балки 0,9 м. Моделирование производилось двумерными конечными элементами одинаковой длины (1 см). Сечения балок 0,001×0,005 м. Балки соединены между собой вдоль длинной стороны сечения. Материал – сталь. Коэффициент внутренних потерь для обеих балок 0,01.
Проведем расчет коэффициентов энергетической связи для двух вариантов соединения балок (рис. 1). Для каждого варианта расчета гармоническая нагрузка 1 Н прикладывалась поочередно к каждой балке на расстоянии 0,1 м от края, всегда перпендикулярно к балке.
а
Рис. 1. Варианты соединения двух балок: а - угол равен 90°; б - угол равен 45°
б
Fig. 1. Variation of two beams coupling: a - 90° angle; b - 45 ° angle
Составим СУЭБ для этой системы. Для удобства при E введем второй индекс так, что запись E 12 будет означать энергию первой подсистемы при введении энергии во вторую [15]. Аналогично - для оставшихся E 11 , E 21, E 22 . После чего СУЭБ в матричном виде будет выглядеть так:
П 1 +П 12
—П 12
-П 21 E 11
П +П 21 JL E 21
E 12 = П ,
E 22 J L °
П J
а уравнения системы примут вид
П 1 E 11 + П 12 E 11 П 21 E 21 = ,
П 2 E 21 + П 21 E 21 — П 12 E11 = °,
.
П 1 E 12 + П 12 E 12 —П 21 E 22 = °,
П 2 E 22 +П 21 E 22 —П 12 E 12 = /^
.
Зная коэффициенты внутренних потерь балок, из расчета по МКЭ найдем полные энергии колебаний подсистем. Для этого необходимо провести два расчета, поочередно вводя энергию в каждую балку.
Таким образом, коэффициенты энергетической связи η 12 и η 21 могут быть вычислены из следующих выражений:
П 12 =
E 21 ( П 2 E 22 + П 1 E 12 )
E 11 E 22
E 12 E 21
П 21 =
E 12 ( П 1 E 11 +П 2 E 21 )
E11E 22
E 12 E 21
Результаты расчета коэффициентов энергетической связи для двух вариантов соединения балок представлены на рис. 2 и 3.
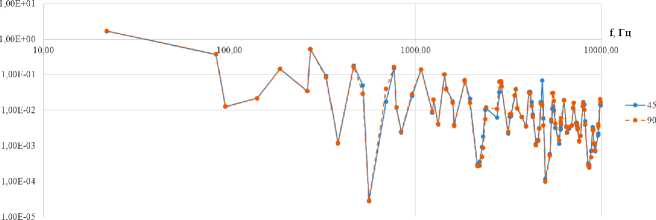
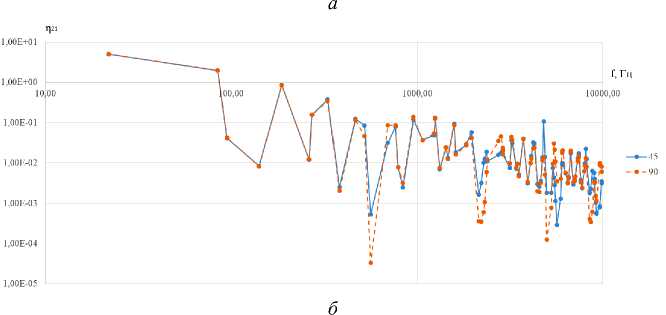
Рис. 2. Коэффициент энергетической связи в зависимости от частоты: а – η12; б – η21
Fig. 2. Coupling loss factor depending on the frequency: a – η12; b – η21
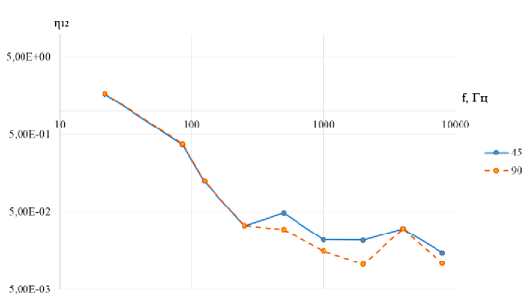
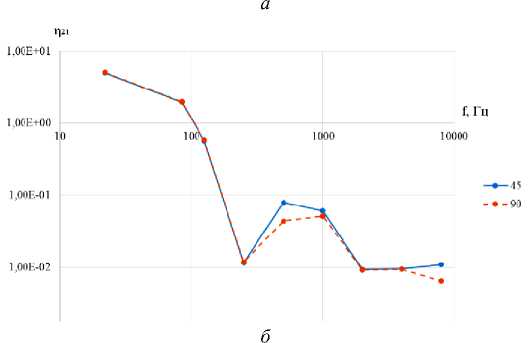
Рис. 3. Коэффициенты энергетической связи по третьоктавным частотным диапазонам: а – η12; б – η21
Fig. 3. Coupling loss factors in 1/3 octave frequency bands: a – η12; b – η21
Результаты
Из графиков, приведенных на рис. 2 видно, что значения коэффициентов энергетической связи двух балок при переходе энергии из первой во вторую η12 и, наоборот, из второй в первую η21, незначительно возрастают при уменьшении угла между балками. В то же время разница в значениях η 21 для случаев соединения балок под углами 90° и 45° более заметна на определенных собственных частотах.
Однако если просуммировать значения коэффициентов энергетической связи в третьоктав-ных полосах частот, то подобные выводы становится сделать сложнее. Это говорит о том, что к осреднению результатов следует подходить с осторожностью и не ограничиваться анализом осредненных значений.
Заключение
Получены значения коэффициентов энергетической связи двух балок по результатам двух вариантов расчета. В первом варианте балки соединялись под прямым углом, во втором – угол, образуемый двумя балками был равен 45°. Сравнительный анализ проведенных расчетов показал, что уменьшение угла между балками незначительно влияет на значения коэффициентов энергетической связи двух балок. Полученные результаты позволяют предположить, что для более сложных систем, таких как изогридные (или анизогридные) силовые конструкции космических аппаратов, образованные пересечением ребер под определенным углом, коэффициенты энергетической связи также будут меняться незначительно при изменении угла сопряжения ребер. Это позволило бы не проводить дополнительные расчеты и измерения за счет использования в расчетах уже известных коэффициентов энергетической связи. Данное предположение требует дальнейшего подтверждения на примере анализа более сложных систем.
Список литературы Определение коэффициентов энергетической связи балок, соединенных под углом
- Lyon R. H., DeJong R. G. Theory and Application of Statistical Energy Analysis (Buttersworths-Heimann), Boston, MA, 1995.
- Fankhauser N. Statistical Energy Analsysis for Room Acoustics: Master`s Thesis. Graz: Signal Processing and Speech Communications Laboratory Graz University of Technology, 2016. 127 p.
- Johansson D., Comnell P. Statistical Energy Analysis software: Master`s Thesis in the Master’s programme in Sound and Vibration. Göteborg: Chalmers University of Technology, 2010. 89 p.
- Piersol A. G., Paez T. L. Harris’ shock and vibration handbook, The McGraw-Hill Companies, Inc. 2010. 1199 p.
- Equivalent curvatures broadband Insertion Loss simulation technique coupling Virtual SEA and BEM/FEM approaches / J.-F. Rondeau, A. Duval, J. Monet-Descombey, L. Dejaeger // Conference: Internoise: Innsbruck, Austria, 2013. 10 p.
- Xiaoyan Yan. Energy Finite Element Analysis Developments for High Frequency Vibration Analysis of Composite Structures. PhD thesis, The University of Michigan, Ann Arbor, 2008.
- Burroughs C. B., Fischer R. W., Kern F. R. An introduction to statistical energy analysis // Journal of the Acoustical Society of America. 1997. Vol. 101(4). P. 1779–1789.
- Кравчуновский А. П. Обзор методов анализа микровибраций // Космические аппараты и технологии. 2023. № 4. C. 243–250.
- Simmons C. Structure-Borne Sound-Transmission through Plate Junctions and Estimates of Sea Coupling Loss Factors Using the Finite-Element Method // Journal of Sound and Vibration. 1991. Vol. 144(2). P. 215–227.
- Steel J. A., Craik R. J. M. Statistical Energy Analysis of Structure-Borne Sound-Transmission by Finite-Element Methods // Journal of Sound and Vibration. 1994. Vol. 178(4). P. 553–561.
- The Use of Wave-Absorbing Elements for the Evaluation of Transmission Characteristics of Beam Junctions / K. DeLanghe, P. Sas et al. // Journal of Vibration and Acoustics-Transactions of the ASME. 1997. Vol. 119(3). P. 293–303.
- Fredo C. R. A SEA-like Approach for the Derivation of Energy Flow Coefficients with a Finite Element Model // Journal of Sound and Vibration. 1997. Vol. 199(4). P. 645–666.
- An Approach for Evaluating Power Transfer Coefficients for Spot-welded Joints in an Energy Finite Element Formulation / N. Vlahopoulos, X. Zhao et al. // Journal of Sound and Vibration. 1999. Vol. 220(1). P. 135–154.
- Грушецкий И. В., Смольников А. В. Применение метода конечных элементов для расчета коэффициентов энергетической связи, используемых в статистическом энергетическом методе, на примере углового соединения балок // Техническая акустика. 2004. № 6. С. 1–10.
- Hopkins C. Statistical energy analysis of coupled plate systems with low modal density and low modal overlap // Journal of Sound and Vibration. 2002. Vol. 251(2). P. 193–214.


