Определение координат точечной цели при подповерхностном зондировании

Целью подповерхностного зондирования является обнаружение, определение местоположения и классификация объектов и структур искусственного и естественного происхождения, находящихся под слоем диэлектрического материала (почва, скальные породы, пресная или морская вода, биологические ткани и т.д.). Начало работ по подповерхностному зондированию как в отечественной, так и в зарубежной истории восходит примерно к 60-70-м гг. XX в. [1, 2, 3]. Результаты этих работ привели к появлению различных вариантов георадаров. Анализ научнотехнической и патентной литературы показывает, что в настоящее время существует много способов и устройств подповерхностного зондирования.

Большое значение имеют задачи определения координат точечной цели при подповерхностном зондировании радиолокационными методами объектов, включая гидролокацию, георадиолокацию и, в частности, ультразвуковые исследования (УЗИ) состояния внутренних органов и структур человека.

Метод георадиолокационного подповерхностного зондирования (в общепринятой терминологии — георадиолокация, в англоязычной литературе этот метод называется «Ground Penetrating Radar» или GPR) основан на исследовании эффектов распространения электромагнитных волн в среде [4]. Метод гидролокации основан на использовании звуковых волн в водной среде. Идея метода заключена в определении положения подводных объектов при помощи звуковых сигналов, излучаемых самими объектами (пассивная локация) или возникающих в результате отражения от подводных объектов искусственно создаваемых звуковых сигналов (активная локация) [5]. Метод УЗИ основан на излучении и приеме отраженных уль

тразвуковых волн при распространении в биологических тканях и используется в медицине для диагностики и терапии [6]. Существуют и другие методы зондирования, например методы дистанционного зондирования Земли при решении горно-технологических задач [7] и др.

В настоящее время вышеперечисленные методы дают возможность получить относительно высокую разрешающую способность при определении размеров подповерхностного объекта [8], но, тем не менее, не всегда позволяют с требуемой точностью определить координаты точечной цели, расположенной в подповерхностном пространстве. Например:

• -    известен радар подповерхностного зондирования [9]. Недостатком известного радара является низкая точность определения координат точечной цели;

• -    известно устройство дистанционного зондирования подповерхностных слоев почвы [10]. К недостаткам известного устройства можно отнести низкую точность измерения, что обусловлено неавтоматизированным отсчетом координат по двумерному изображению подповерхностного пространственно-временного сигнала на экране электроннолучевого индикатора, а также нереальность его использования при подповерхностном зондировании внутренних органов человека и животных в процессе ультразвуковых исследований.

Целью данной работы стало исследование возможности повышения точности определения координат точечной цели при подповерхностном зондировании.

Рассмотрим случай, когда на поверхности исследуемого пространства, в котором находится точечная цель, расположены две антенны.

Пусть антенна в позиции x₀ является приемоизлучающей, а другая антенна, в позиции x 1 , только приемной. В общем случае точечная цель А находится в точке с координатой x_A, сдвинутой по оси x относительно координаты х₀ и не совпадающей ни с одним дискретным положением разнесенных антенн. Глубину расположения цели А обозначим z_A.

Геометрия подповерхностного зондирования цели А для случая двух приемных антенн приведена на рис. 1. Время движения зондирующего сигнала от точки X ; до цели

• t , = -^^x^- xA ⁾² + zA                                         (1)

где i=1, 2, отличает положения антенн, разнесенных относительно друг друга, V- скорость распространения зондирующего сигнала в подповерхностном пространстве.

Если x a = x о , глубина залегания точечной цели z_A=Vt₀ , что соответствует физическим представлениям. Для рассматриваемого общего случая геометрическим местом точек, равноудаленных на измеренное значение Vt₀ относительно x₀, служит окружность. Это значит, что отражающий объект может находиться в любой точке этой окружности. Аналогично для x 1 геометрическим местом точек, равноудаленных на измеренное значение Vt 1 , будет являться окружность с центром в точке x 1. Искомые координаты x_A, z_A определяются в точке пересечения окружностей. Для нахождения координат x_A, z_A необходимо решить систему уравнений

| ( xA - x о )² + zA ² = (Vt о )² [ ( xA - x i )² + zA ² = (Vt i )².

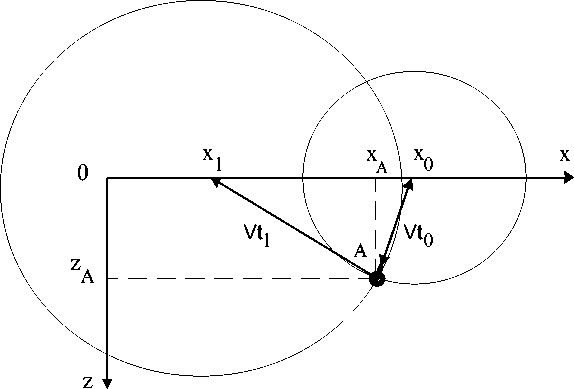
Рис. 1. Геометрия подповерхностного зондирования при расположении в исследуемом пространстве точечной цели для двух приемных антенн

Общая точка этих уравнений имеет искомые координаты

X a = ( t 0 - t 1 ) + К 2,                                                  (3)

К 1

Z A =V (Vt i )² - ( X a - X i )²,                                            (4)

2( x , - x o ) V²

здесь K1=

- постоянный коэффициент с размерностью [с2/м], K2= (x, + хo ) /2 — по стоянный коэффициент с размерностью [м]. В (4) используется положительное значение ква- дратного корня.

Источником информации при определении (3) и (4) является измерение переменных t0 и t,. Наиболее перспективно использовать для измерительных целей и последующей обработки цифровые методы, которые сопровождаются погрешностями меры, преобразования и погрешностью дискретного определения переменных t0 и t,, что приводит к погрешности координат xA и zA. Погрешность меры обусловлена нестабильностью частоты квантующего генератора и, как правило, много меньше погрешности дискретного определения переменных t0 и t,. На погрешность преобразования существенное влияние будет оказывать отношение сигнал/шум на входах триггера. Чаще всего погрешность преобразования удается свести к величине гораздо меньшей погрешности дискретного определения переменных t0 и t1, поэтому погрешности меры и преобразования в настоящей работе не рассматриваются.

При определении xA возникает случайная составляющая Ах:

= 2( t^ - ti^i) + i    i

K 1        K 1

При отсутствии внешних факторов, искажающих результат измерения, в частности, шумов, природа случайных составляющих ^ и ^, заключена в произвольной кратности t0 и t, периоду квантующей последовательности tкв. Поскольку начало измеряемых интервалов времени, совпадающее по времени с импульсом запуска, и частоту квантующей последовательности легко синхронизировать от общего генератора, то имеет место только погрешность дискретности, проявляющаяся в конце измеряемого интервала. Структурная схема измерения длительностей интервалов времени t0 и ti приведена на рис. 2. Цифровые измерители длительности интервалов времени широко известны и достаточно глубоко описаны, например, в [11].

Синхронизатор (С) формирует бесконечную последовательность коротких электрических импульсов, следующих с частотой квантования f кв . Этими импульсами запускается передатчик (П), где частота f_кв понижается до частоты зондирующих импульсов, которые через антенный коммутатор (АК) возбуждают приемопередающую антенну (ППА). В этот же момент времени запускаются по второму входу первый и второй цифровые измерители длительности интервала времени. Зондирующий сигнал излучается ППА в исследуемое подповерхностное пространство. Прием сигнала, отраженного точечной целью, осуществляется ППА и приемной антенной (ПА). Для георадиолокационного подповерхностного зондирования, как правило, используют антенны различных глубин зондирования, от 30 до 0, 8 м [12]. Для проведения медицинских УЗИ служат антенны, выполненные из пьезоэлементов с центральной частотой спектра 2, 5 – 15 МГц, позволяющих проводить зондирование на глубину 0, 25 – 0, 02 м [13].

АК обеспечивает переключение зондирующих (излучаемых) и принимаемых сигналов в режиме прием – передача для развязки достаточно мощного зондирующего сигнала с выхода П от входа первого малошумящего усилителя (МШУ1). Принятый ППА сигнал усиливается МШУ1 и детектируется. Далее сигнал с выхода первого детектора (Д1) поступает на первый вход первого цифрового измерителя длительности интервала времени, что останавливает подсчет квантующих импульсов его счетчиком (СЧ). Поскольку длительность интервала времени, измеряемого в первом цифровом измерителе длительности, формируется в результате прохождения импульсом двойного расстояния до цели, то для получения значения t 0 необходимо подсчитанные им квантующие импульсы разделить на два. Сигнал с ПА обрабатывается аналогично.

Измеренное значение t₀ в виде числа N₀ с выхода делителя частоты на два (ДЧ) поступает на второй вход сумматора (Сум). Измеренное значение t₀+t 1 в виде числа N с выхода второго цифрового измерителя длительности интервала времени поступает на первый вход Сум, где из него вычитается N₀. На выходе Сум появляется число N 1 =N-N₀.

Случайные составляющие ^ и ^ распределены по закону равномерной плотности в интервале (0 - t_кв) и имеют математические ожидания и дисперсии [14]: M [ ^ ]=M [^ ]=t_кв/2,

D [ ^ ]=D [ г „ ]= t1112.

Следовательно, математическое ожидание случайной составляющей Δx

M [ A r ] = t кв ⁽ K^ t ¹ ) .

Из этого следует, что при t₀ = t 1 , когда точечный объект расположен на нормали к поверхности строго между элементами антенной решетки, отсутствует смещение оценки координаты x_A, вызванное погрешностью дискретного преобразования. Здесь и далее ограничимся тем, что цель по координате x находится в пределах интервала [x₀- x i ]. Тогда оценка будет максималь-

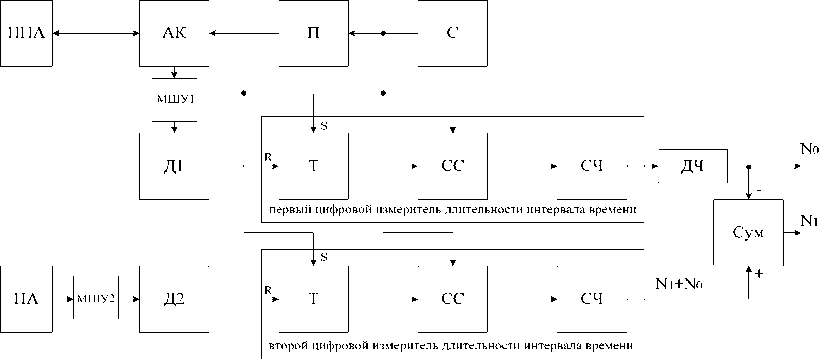
АК – антенный коммутатор, Д1 – первый детектор, Д2 – второй детектор, ДЧ – делитель частоты на два, МШУ1 – первый малошумящий усилитель, МШУ2 – второй малошумящий усилитель, П - передатчик, ПА – приемная антенна, ППА – приемопередающая антенна, С – синхронизатор, Сум – сумматор, СС – схема совпадений (цифровое «И»), СЧ – счетчик, Т – триггер RS

Рис. 2. Структурная схема измерения длительностей интервалов времени t0 и t1

но смещена при расположении объекта на нормалях в позициях x0 или x1, когда разность по модулю (t0-t1) пропорциональна z - z2 + (x0 - x1)2 . Однако при больших глубинах, когда zА >> (x0-x1), можно пренебречь смещением оценки координаты xA, вызванным дискретным преобразованием.

Дисперсия погрешности дискретного преобразования по координате xA определяется по формуле t2               2

D ^] = 3K1 2 ( 1 0 - 1 * ) .                                     (7)

Из выражения (7) видно, что при расположении цели строго на нормали к поверхности в точке середины отрезка x0 – x1 дисперсия равна нулю, если же цель расположена на нормалях к поверхности в позициях x0 или x1, то дисперсия будет максимальна.

Рассмотрим погрешности дискретного определения координаты глубины zA, содержащей случайные составляющие в результате измерения t1 и вычисления xA. Для этого воспользуемся разложением корня квадратного выражения (4) в биномиальный ряд с ограничением линейным приближением вида V1 + a «1 + 0 при |a| < 1.

Приближенная оценка глубины zA производится по формуле z ≈Vt +(xA -x1)2 .                                                (8)

^{A 1}      2 Vt 1

Приближение (8) для x A =x 0 , когда Δx максимально, и при небольших глубинах залегания точечного объекта, когда z A ≤ (x₀ - x 1 ) , приводит к относительной погрешности измерения глубины, не превышающей 5,7 %.

В выражении (8) две переменные содержат случайную составляющую – ξ1, возникающую при измерении времени распространения сигнала, и полученное выше значение Δx.

Таким образом, при определении zA проявляется случайная составляющая Δz:

Az = V6, +

1        _x 2

2 ( t , + 6 , ) ⁽ A

+ 2 xAx 1 + x 1 ² + A x ² - 2 A xxA - 2 A xx 1 )

Математическое ожидание случайной составляющей Δz:

M [ A z ] = 1 Vt ₊ !_ ( х_{д +} x ) ² ₊ Utt о ^- t . ) _x •

² к⁸ 4Vt ² + t . t„ ⁽ A ¹ ) VK 1 ( t . + t . t„ )

/

•

t_кв ( t ₀

-

t l ) t l ⁺

V

tкв

-

K 1

( ^xA ⁺ x l

кв

.

При t 0 = t 1 , когда точечный объект расположен на нормали к поверхности строго между элементами антенной решетки, математическое ожидание:

M [ A z ] = ¹ Vt_Ke + — t k ^{+ 2} t ¹ (x , + x )². кв            2               A 1

²        4 V t l ⁺ t l t_K6

Дисперсия погрешности дискретного преобразования по координате zA определяется по формуле

D [ A z ] = V—кв - +

2 t_кв

V^{2 (} - 1 1„ ⁺ t ^{2 ) 2}

x4+Ax¹x¹+x⁴   ( tn - t ) 2 ( x 2 + x 2 ) Г (6 t + 6 1, J2 - 3t 2 - ² 1, ²1

X a + “ x A x i + x i     v 0     1 / \ A 1 '^'- 1 кв '        1 кв |

48                      45 K 1

При t 0 = t 1

V² t_K■    t ke ( x A + 4 x A x 2 + x 4 )

= —^к— +—--------

¹²        4 8 V ² ( t1t_K6 + 1 2 ) 2

V ² t к ² в

₊ t KB

V ² t 1 ⁴

Выражения (10) и (12) для общего случая, когда t0 ≠ t и tкв<

M[Az ]= 1 VtKB+ -1- (xA+x, ) 2       2Vt1

2+tkB (10 - t)Г 2 ttkB (10 - tx)     ,        J +   vk 112    з    к 1       t1 (xA+x1) ’          ( )

Такое упрощение при условии, что tкв<1, позволит определить погрешность дискретного преобразования по координате zA с относительной погрешностью не более 0, 3 %.

На рис. 3 приведен график зависимости математического ожидания погрешности дискретного преобразования по координате zA от изменения глубины zA при V=1500 м/с, tкв=1*10^-7 c, x0=0, x =0,1 м, xА=0,1 м. На рис. 4 можно видеть зависимость дисперсии погрешности дискретного преобразования по координате z_A от изменения глубины z_A при тех же условиях, что и выше. На рис. 5 изображен график зависимости дисперсии погрешности дискретного пре-

Рис. 3. График зависимости математического ожидания погрешности дискретного преобразования по координате zA от изменения глубины zA

Рис. 4. Зависимость дисперсии погрешности дискретного преобразования по координате zA от изменения глубины zA образования по координате xA от изменения координаты xA при тех же условиях, что выше, и zA=10 м.

Как видно на рис. 3, математическое ожидание погрешности дискретного преобразования по координате zA при увеличении глубины zA уменьшается экспоненциально.

Зависимость же математического ожидания погрешности дискретного преобразования по координате x_A от изменения координаты x_A имеет линейный вид (это видно из формулы (6)) и при t0 = t1 , когда точечный объект расположен на нормали к поверхности строго между элементами антенной решетки, равна нулю.

Дисперсия погрешности дискретного преобразования по координате zA от изменения глубины z_A резко уменьшается при увеличении глубины на небольших глубинах залегания точечного объекта и затем достигает линейной зависимости (с увеличением глубины не изменяется и при оговоренных выше условиях имеет значение 1, 125*10^-8 м²) (рис. 4).

Дисперсия погрешности дискретного преобразования по координате xA от изменения координаты x_A описывается параболической функцией и при расположении точечной цели на нормали к поверхности строго между элементами антенной решетки равна нулю (рис. 5).

Рис. 5. Зависимость дисперсии погрешности дискретного преобразования по координате xA от изменения координаты Хд

Таким образом, в настоящей работе получена оценка погрешностей дискретного определения координат точечной цели, влияющих на точность определения координат точечной цели при подповерхностном зондировании.

Основные выводы по проделанной работе:

• -    при t₀ = t₁, когда точечный объект расположен на нормали к поверхности строго между элементами антенной решетки, отсутствует смещение оценки координаты х_д, вызванное погрешностью дискретного преобразования. Учитывая ограничение, что цель по координате x находится в пределах интервала [x₀- х₁], можно констатировать, что оценка будет максимально смещена при расположении объекта на нормалях в позициях х₀ или x_b когда разность по модулю (t₀-t₁) пропорциональна z - д/z²+ (xо — Х1)². Однако при больших глубинах, когда z_A >> (x₀-x₁), можно пренебречь смещением оценки координаты х_д, вызванным дискретным преобразованием;

• -    дисперсия погрешности дискретного преобразования по координате х_д от изменения координаты х_д описывается параболической функцией и при t₀ = t₁ аналогично математическому ожиданию равна нулю; если же цель расположена на нормалях к поверхности в позициях х₀ или х₁, то дисперсия будет максимальна;

• -    математическое ожидание погрешности дискретного преобразования по координате zA от изменения глубины zA уменьшается экспоненциально;

• -    дисперсия погрешности дискретного преобразования по координате zA от глубины zA резко уменьшается при увеличении глубины на небольших глубинах залегания точечного объекта и затем достигает линейной зависимости (с увеличением глубины не изменяется и имеет постоянное значение).

Представляет теоретический и практический интерес распространение полученных результатов на определение размеров и координат протяженных подповерхностных образований, а также использование многоэлементных приемопередающих антенных решеток.

Работа выполнена при поддержке Красноярского краевого фонда поддержки научной и научно-технической деятельности по гранту КФ-11 (2009 г.) и при поддержке программы развития Сибирского федерального университета.

• 1.    Финкельштейн М. И. Радиолокация слоистых земных покровов / М. И. Финкельштейн, В. Л. Мендельсон, В. А. Кутев – М.: Сов. радио, 1977. – 174 с.

• 2.    Cook J. C. Proposed monocycle-pulse very high frequency radar for airborne ice and snow measurement / J.C. Cook // Trans. AIEE Commun. Electron. № 79, 1960, 588-594.

• 3.    Хармут Х. Ф. Несинусоидальные волны в радиолокации и связи: Пер. с англ. – М.: Радио и связь, 1985. – 376 с., ил.

• 4.    Георадиолокационное подповерхностное зондирование [Электронный ресурс] // Прин. – 2007.– Режим доступа: http://www.prin.ru/articles/147/

• 5.    Тюрин А. М. Основы гидроакустики / А. М. Тюрин, А. П. Сташкевич, Э. С Таранов. – М.: Судостроение, 1966. – 296 с.

• 6.    Хилл К. Применение ультразвука в медицине: Физические основы: Пер. с англ. / Под ред. К. Хилла. – М.: Мир, 1989. – 568 с., ил.

• 7.    Потапов В. П. Методы решения горно-технологических задач с использованием данных дистанционного зондирования Земли / В. П. Потапов, О. Л. Пястунович // Журнал Сибирского федерального университета. Серия: Техника и технологии. – 2008. – Т. 1, № 4. – C. 359-365.

• 8.    Гринев А. Ю. Вопросы подповерхностной радиолокации / Под ред. А. Ю. Гринева. – М.: Радиотехника, 2005. – 416 с.: ил.

• 9.    Свидетельство на полезную модель 22826 Российская Федерация, МПК⁷ G01N29/24. Радар подповерхностного зондирования / К. П. Янковский, Л. А. Ведешин, В. В. Егоров. – № 2001133926/20 ; заявл. 20.12.01 ; опубл. 27.04.02.

• 10.    Пат. 2154845 Российская Федерация, МПК⁷ G 01 V 3/16, G 01 V 3/17. Устройство дистанционного зондирования подповерхностных слоев почвы / Е. Э. Чернышов, Н. А. Кротов, Л. Ю. Астанин, В. И. Норкин. – № 97118586/28; заявл. 11.11.97 ; опубл. 20.08.2000.

• 11.    Чмых М. К. Цифровая фазометрия / М. К. Чмых. – М.: Радио и связь, 1993. – 184 с.

• 12.    Помозов В. В. Геофизические приборы нового поколения / В. В. Помозов, Н. П. Семейкин, Б. В. Эквист и др. // Мир геотехнологий. – 2008. – № 44.

• 13.    Осипов Л. В. Ультразвуковые диагностические приборы: Практическое руководство для пользователей / Л. В. Осипов. – М.: Видар, 1999. – 256 с.: ил.

• 14.    Вентцель Е. С. Теория вероятностей / Е. С. Вентцель. – М.: Наука, 1969. – 576 с.: ил.

Determination of Coordinatesof the Point Target at Subsurface Sounding

Ivan N. Shevchenko

Siberian Federal University,79 Svobodny, Krasnoyarsk, 660041 Russia

We consider the coordinates of point target in the subsurface probing through radiation transmitting and receiving antenna of the probe signal in the subsurface space and reception reflected from the point target signal is the same antenna and the other receiving antenna, separated by some distance.

We estimate the statistical characteristics of determining the coordinates of the point target.