Определение критической нагрузки межслойного дефекта, возникающего при сжатии кольца

Устойчивость конструкций с дефектами типа расслоений, в частности тонкостенного кольца, остается наиболее интересной и малоизученной из всех проблем механики деформированного твердого тела [1]. В работе рассмотрена задача о нелинейной устойчивости тонких расслоений, расположенных вблизи внутренней поверхности сжатого кольца. Задачи об устойчивости элементов конструкций с различными дефектами рассмотрены в работах [2-6].

Постановка задачи

Рассмотрим кольцо толщиной H и радиусом R под действием внешнего давления q (рис. 1). Вблизи внутренней поверхности многослойное кольцо имеет один межслойный дефект типа расслоение толщиной h >>  H , который теряет устойчивость хлопком при сжатии кольца. Дефект на той части кольца, где он не соприкасается с кольцом, нагружен в окружном направлении сжимающими силами P . Для решения задачи устойчивости дефекта типа расслоение в работе использована приближенная теория пологих оболочек с помощью линеаризованных уравнений. Получение точного решения для данного случая не представляется возможным.

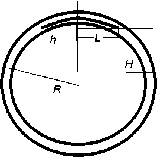
Рис. 1. Кольцо с межслойным дефектом

Материал дефектного участка изотропный. Длина дефекта мала по сравнению с длиной окружности, дефект симметричен относительно оси z . Начало координат расположено так, что на границе дефектного участка при 5 = L значение z = 0 . В ненагруженном состоянии дефект не отслаивается от кольца. Так как межслойный дефект соприкасается с кольцом, внутренние усилия постоянны и равны приложенной силе P , не зависят от размеров самого кольца, межслойный дефект можно рассматривать как пологую арку. Координата 5 изменяется по средней линии пологой арки на дефектном участке 0 < 5 < L , L — длина дефектного участка и на участке 0 < 5 < 51, где дефект не соприкасается с кольцом, 51 — точка соприкосновения дефекта с кольцом. Изгиб дефекта сопровождается возникновением внутренних нормальных и поперечных усилий N, Q и изгибающим моментом M (рис. 2). Необходимо определить пере- мещение дефекта и условия, при котором происходит потеря устойчивости расслоения.

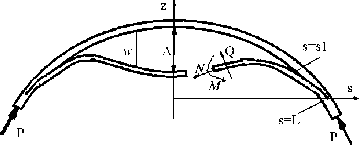
Рис. 2. Изгиб дефекта типа расслоение

Недеформированная форма кольца описывается функцией z ( s ). В работе рассмотрен только один случай поведения дефекта — кривизна функции z ( s ) на дефектном участке везде отрицательна.

Определены прогибы дефекта, перемещение вершины дефекта А в зависимости от сжимающей нагрузки P . Линеаризованные уравнения получены при следующих допущениях:

• 1.    Изменения геометрических размеров кольца считаются пренебрежимо малыми.

• 2.    Силы трения между дефектными участками не учитываются.

• 3.    Связь между внутренним изгибающим моментом и поперечным изгибом при потери устойчивости описывается линейными зависимостями теории изгиба арок, основанной на гипотезе плоских сечений.

• 4.    Ось дефектного участка без растяжения.

Решение задачи

Рассмотрим равновесия элемента арки в отклоненном состоянии от исходного (рис. 2). Выделим элемент AB и все силы, приложенные к нему. Радиальные перемещения будем считать w = w(s) малыми величинами, v . dw „, . d2w . d3w величины w (s) = —, w (s) = —- w (s) = —— — величинами первого ds          ds2          ds3

порядка малости. Касательные перемещения точек дефекта и будем считать бесконечно малыми. В соответствии с идеей линеаризованных уравнений будем учитывать только величины первого порядка малости и пренебрегать величинами высшего порядка малости. При составлении системы нелинейных дифференциальных уравнений вводим следующие допущения:

w = S ;sin( S ) = S ;cos( S ) = 1;sin( S + d S );cos( S + d S ) = 1, (1)

где w — прогиб по оси z , S — угол поворота. В силу допущения изгибающий момент и поперечная сила связаны между собой следующими зависимостями:

, „          ,, , dN ■ dw

M = EJS;Q = (EJS );N = — ;S = w = —, ds          ds где EJ — изгибная жесткость. Положительное направление усилия, изгибающего момента, и перемещения представлены на рис. 2. Проектируя на оси S все силы, получим следующее уравнение

• - N cos( S ) - Q sin( S ) - ( N + dN ) cos( S + d S) + ( Q + dQ )sin( S + d S ) = 0 .

Учитывая допущения 1, получим

• - N - QS + N + dN + QS + SdQ + QdS + dQdS = 0.

Пренебрегаем величиной высшего порядка малости dQdS и учитывая преобразование SdQ + QdS = (QS) , получим N + (QS) = 0 . Исключая слагаемое (QS) = [(EJw ) w ] как содержащее произведение двух величин первого порядка малости, окончательно получим первое дифферен- циальное уравнение dN=о.

сумму всех мо-

ds

Приравниваем к нулю проекцию всех сил на ось z и ментов, исключив величины высших порядков малости получим два уравнения d2M ds2

—

d 2 z - d 2 w I N = 0.

ds ds .

Изгибающий момент в тонкой упругой арке связан соотношением уп- ругости d2 w _ M

ds2 EJ , где EJ — изгибная жесткость арки в ее плоскости. Из уравнения (2) и требования N _ P при s _ si, получаем N _ P на интервале 0 < s < si. Граничные условия для уравнений (3) и (4) аналогичны граничным условиям задач изгиба. Если радиальные перемещения на торце не стеснены, то поперечная сила равна нулю Q _ (EIS ) _ 0 и угол поворота равен ну лю S _ 0, dMdw при s _ 0, ---_ 0;— _ 0;

dsds

при s _ s i , M _ 0; w _ 0 ;.

Для удобства введем следующие обозначения k2 _ —, f (s) _ d"Z,

EJds где z(s) функция от s . Функцию f (s) будем считать непрерывной на участке 0 < s < si. Исключив w _ w(s) из уравнения (3) и (4), можно по- лучить одно уравнение с одним неизвестным 75

d ² M

—

ds ² d 2 M ds ²

MP

Pf ( 5 ) +---= 0 или

EJ

+ k 2 M = Pf ( 5 ).

Определим решение уравнения (6) для изгибающего момента в виде

M = EJ k^f ( n )sin k ( 5 — n ) d n

- 0

—

k cos k5 r .

---— f ( n )sin k ( 5 1 — n ) d n , cos k5 1 0

которой удовлетворяет граничным условиям (6), переменная 0 <  n <  5 1.

Для определения перемещения проинтегрируем уравнение (4) дважды. Проинтегровав уравнение (4), получаем

s

s

dw r 5

— = j k j f ( n )sin k ( 5 — n ) d n d⁵   0 - 0

—

k cos ks^s 1       .

----— I f ( n )sin k ( 5 1 — n ) d n d5 . cos k51 0

Эффективным способом вычисления двойных интегралов является сведение их к однократным интегралам. Для вычисления двойного интеграла введем обозначение

s

s

s

1 1 = j k j f ( П )sin k ( ^s — П ) d n d5 = k j f ( n )1 { — cos k ( 5 — n ) } | 0 d n 0 _ 0                             _          0 ^-                                   -

s

s

,

- j [ f ( n ) { cos k n — cos k ( 5 — П ) } ] d n - j [ f ( n ) { 1 — cos k ( 5 — n ) } ] d n

где cos k n = 1.

1 2 = 5 k cos k⁵ f ( n )sin k ( 5 1 — n ) d n d5 = -sin k⁵ - f f ( n )sin k ( 5 1 — n ) d n d5 .

₀ cos ks 1 ₀                           cos ks 1 ₀

Окончательно получаем

s

ddw = j f ( n ) 1 — cos k ( 5 — n ) d n

—

s 1

sin k5 f .

---— f ( n )sin k ( 5 1 — n ) d n . cos k5 1 0

Проинтегрировав выражение (7), получим

—

s 1

sin k5 f .

---—I f ( n )sin k ( 5 1 — n ) d n d5 .

cos k51 0

Для вычисления двойного интеграла введем обозначение

ss

ss

I 3 - jj f ( n ) [ 1 — cos k ( 5 — n ) ] d n d5 - j d n j f ( n ) [ 1 — cos k ( 5 — n ) ] d5 -

5      Г

= j f (n) 5 +

0         - где sin kn = kn •

sin k ( — 5 + n )

k

1 ^s

1₀ d n = — [ [ k5 — sin k ( 5 — n ) — sin k ] d n ,

0 k0

1 4 = J sin k\ j f ( П )sin к ( s 1 — n ) d n ds = ^C0S(,^) | 0 j f ( n )sin к ( s 1 — n ) d n

0 cos ks 10                            к cos ks 1    0

= ¹ cos ^kS f f ( n ) sin к ( s 1 — n ) d n .

к cos ks 1 0

Окончательно получим перемещение в виде w = w(0)+Iff (n)[к (s—n)—sin к (s—n )dn — 1— cos kS (f (n )sin к (s1 —n) dn (8) к         X                         к cos ks1 0

В точке, где расслоение соприкасается с кольцом s = s 1 , w = 0 , из уравнения (8) получаем

₁ s 1                                                 ₁ s 1

—

---------х к cos( ks 1)

W (0) = - J f (n)[к (s1 — n)] dn — ~ J f (n )sin( s1 — n) dn х J f (n )sin(к(s1 — n)dn + kc00SkkS1) J f (n)sin(s1 — n)dn

Окончательно уравнение запишем в следующем виде:

А = w (0) = _к co! _{ks 1}) J f ( n )sin( к ( s 1 — n ) d n — | J f ( n ) [ к ( s 1 — n ) ] d n     (9)

Найдем решение уравнения (7), удовлетворяющее граничным услови-dw ям при s = s1, — = 0

ds

[ f ( n ) [ 1 — cos к ( s 1 — n ) ] d n — sin ^1 f f ( n )sin( s 1 — n ) d n = 0

0                              cos ks1 0

Преобразуем подынтегральное выражение с помощью тригонометрических функций разности двух углов. Находим

J f( n )[1 — cos к ( ks 1) cos( k n ) — sin( ks 1) sin( k n ) — -sin^ ^ H sin( ks 1) cos( k n ) +

0                                                  cos( ks 1)

+ ^sin(Ы) cos( ks 1)cos( k n ) d n =--- ¹--- (f ( n )[cos( ks 1) — cos( k n ) d n .

cos( ks 1)                        cos( ks 1) 0

Получим выражение

1 s 1

——- J f ( n )[cos( ks 1) — cos( k n ) d n = 0.

cos( ks 1) 0

Рассмотрев отличное от тождественного нуля решение, приходим к уравнению s1

∫ f ( η )[cos( ks 1) - cos( k η ) d η = 0 . 0

Поведение межслойного дефекта, имеющего отрицательную кривизну, аналогично поведению пологих арок, у которых f (s) = - . Решая урав-R нение (10), получаем s1      1                                                 1 1

( - )[cos( ks 1) - cos( k η ) d η = ( - ) [( ks 1) cos( ks 1) - sin( ks 1)] = 0 .

₀   R                Rk

Рассмотрим решение, отличное от тождественного нуля, получаем ха- рактеристическое уравнение:

( ks 1) cos( ks 1) - sin( ks 1) = 0.

Решив это трансцендентное уравнение с помощью системы MathCad (рис. 3), найдем собственные значения.

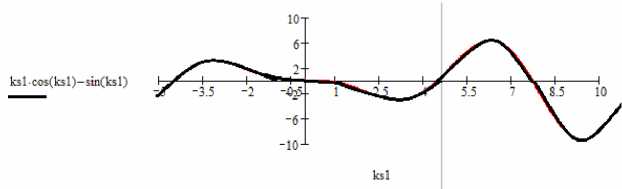
Рис. 3. Нахождение корней уравнения

Наименьшее (первое) собственное значение ks 1 = 4,493 дает критическое значение сжимающей силы. На рис. 4 представлена зависимость параметра нагрузки от величины s 1 , где отслоившейся слой соп рикасае тся с

D               Г          PL ²

кольцом. Зависимость представлена в безразмерном виде ^PL _EJ от

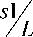
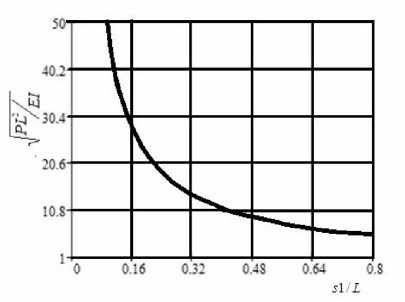
Рис. 4. Зависимость сжимающей силы от величины s 1

Решив уравнение (9), найдем зависимость прогиба в центре дефекта от величины сжимающей нагрузки при f (s) = —- и ksl = 4,493 R

А = —---------{[cos( ksl) — 1]

k ² R cos( ks 1)

—

1 . 1 2 k 2 }=14,83

2          k ² R

.

На рис. 5 представлена зависимость прогиба в центре дефекта от величины сжимающей нагрузки в безразмерном виде ^ PL^E-j от R ^А^'₂ .

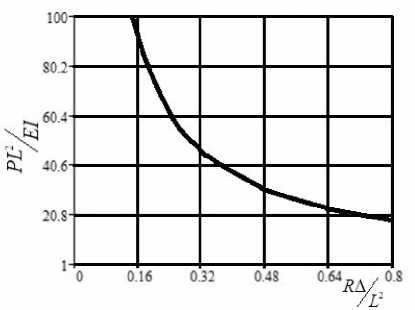
Рис. 5. Зависимость прогиба в центре дефекта от величины сжимающей нагрузки

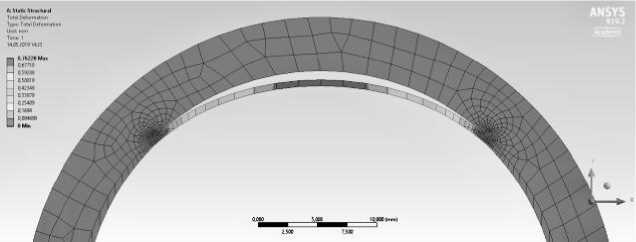
Рис. 7. Деформированное состояние кольца с дефектом (мм)

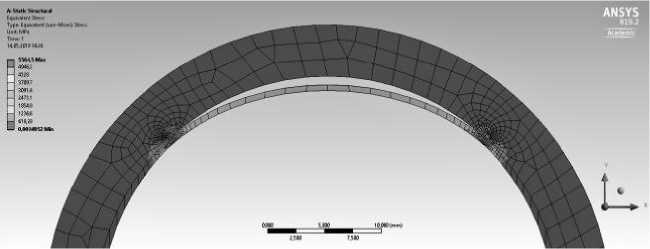
Рис. 8. Напряженное состояние кольца с дефектом (Мпа)

В таблице представлены результаты аналитических и численных значений критической нагрузки дефектов, расположенных под ϕ =75⁰. Диаметр образца составляет 90 мм, 50 мм, материал — сталь. Полученные результаты показали хорошую сходимость между аналитическими и численными значениями.

Таблица

Результаты аналитических и численных значений критической нагрузки дефектов

d (мм)	P кр (кН) (аналит.)	P кр (кН) (числен.)
90	21,9	21,5
50	23,6	23,1

Заключение

При потере устойчивости поведение тонких круговых отслоений становится качественно другим по сравнению с поведением стержней и пластин. Построена уточненная математическая модель, позволяющая прогнозировать потерю устойчивости тонкостенных элементов конструкций, на примере колец с дефектами из слоистых изотропных материалов, основанная на уравнениях теории пологих тонкостенных арок. Определены верхняя критическая нагрузка, прогиб в центре дефекта от величины сжимающей нагрузки. В теории устойчивости оболочек применяют понятия верхней и нижней критических нагрузок. Для определения нижней критической нагрузки следует обратиться к нелинейной теории оболочек.