Определение локального коэффициента теплоотдачи с использованием модели температурного пограничного слоя с конвективной составляющей в полостях вращения ТНА ЖРД
Автор: Зуев Александр Александрович, Пиунов Валерий Юрьевич, Назаров Владимир Павлович, Арнгольд Анна Анатольевна
Рубрика: Расчет и конструирование
Статья в выпуске: 2 т.19, 2019 года.
Бесплатный доступ
Учет особенностей теплоотдачи в проточных частях турбонасосных агрегатов (ТНА) жидкостных ракетных двигателей (ЖРД) является важной задачей. Сопряженная задача течения с теплообменом, в том числе и при вращательных течениях в элементах проточных частей ТНА ЖРД, решается с помощью следующих подходов: численные методы, аналитическое совместное решение уравнений движения и энергии и использование эмпирических уравнений. Наличие теплообмена значительно влияет на рабочие характеристики ТНА ЖРД. При проектировании проточных частей узлов и агрегатов ТНА ЖРД важно учитывать влияние теплообмена и как следствие - температуры потока рабочего тела по длине проточного тракта, в связи с тем, что вязкость напрямую зависит от температуры и определяет потери и режим течения. В агрегатах подачи, особенно при использовании криогенных компонентов топлива, незначительный подогрев рабочего тела может привести к вскипанию компонентов и падению рабочих характеристик. С другой стороны, недостаточная (нерасчетная) температура компонента в проточной части для некоторых видов рабочих тел (например гелеобразных компонентов) приводит к повышенной вязкости и снижению КПД агрегата. При исследовании задачи вращательных течений с теплообменом необходимо совместное решение уравнений движения и энергии в граничных условиях проточных частей ТНА ЖРД с учетом теории пространственного пограничного слоя. Процессы теплоотдачи в энергетических установках во многом схожи, но при анализе и выводе уравнений теплообмена для граничных условий ЖРД существуют определенные отличия. Основные отличия заключаются в следующем: экстремально высокие значения тепловых потоков, температур и давлений, наличие высоких скоростей потоков, начальное турбулентное состояние потоков в активной зоне, рабочие тела могут находиться в газообразном и жидком состоянии, эффекты кривизны поверхности. С использованием аналитического подхода определены уравнения для расчета локальных коэффициентов теплоотдачи в виде критериев Стантона для наиболее важных случаев, реализующихся при течении в полостях вращения ТНА ЖРД. Получены локальные коэффициенты теплоотдачи при прямолинейном течении, вращательных течениях, реализующихся в полостях между рабочим колесом и корпусом турбины и центробежного насоса (течение по закону твердого тела), в подводящих и отводящих аппаратах (течение по закону свободного вихря). Полученные аналитические выражения для локальных коэффициентов теплоотдачи хорошо согласуются с результатами исследований других авторов и имеют практическое применение при расчете характеристик тракта ТНА ЖРД.
Температурный пограничный слой, коэффициент теплоотдачи, интегральное соотношение уравнения энергии, проточная часть турбонасосного агрегата
Короткий адрес: https://sciup.org/147231741
IDR: 147231741 | УДК: 621.454.2 | DOI: 10.14529/engin190203
Текст научной статьи Определение локального коэффициента теплоотдачи с использованием модели температурного пограничного слоя с конвективной составляющей в полостях вращения ТНА ЖРД
Введение. Учет особенностей теплоотдачи в проточных частях турбонасосных агрегатов (ТНА) жидкостных ракетных двигателей (ЖРД) является важной задачей.
Сопряженная задача течения с теплообменом, в том числе и при вращательных течениях в элементах проточных частей ТНА ЖРД, решается с помощью следующих подходов: численные методы, аналитическое совместное решение уравнений движения и энергии и использование эмпирических уравнений. Наличие теплообмена значительно влияет на рабочие характеристики ТНА ЖРД [1].
Использование эмпирического подхода требует проведения большого количества экспериментальных исследований и обобщения результатов. Методам эксперимента л ьных исследований сопряженного теплообмена посвящены работы [2–4]. Данный подход имеет существенные недостатки: не всегда можно обобщить результаты экспериментальных исслед о ваний на подобные процессы и не всегда расчет проводится с требуемой точностью, что также требует допо л нительной верификации результатов.
Методы численного подхода рассмотрены в работах [5–7]. Данный подход требует корректного задания граничных условий и используемых ур а внений. Численные методы исследования используют прямое численное моделирование (метод DNS) и усредненные уравнени я Навье– Стокса и Рейнольдса (RANS метод). Выбор метода зависит от сложности проблемы и т очности результатов. Достаточно часто используется метод RANS с использование моделей k -ε и k-ω турбулентности. При исследовании течения с теплоотдачей в проточных частях ТНА многие авторы уделяют отдельное внимание межлопаточному каналу [8–10] как наибол е е важному элементу проточной части, тем не менее также остро стоит вопрос обеспечения устойчивости и надежности диска ротора.
Аналитический подход позволяет более широко обобщать полученные зависимости на подобные процессы. Аналитические исследования проводились в работах [11–13]. Анали т ические методы, как правило разрабатывались для прямолинейного равномерного течения и имеют ряд ограничений. В наиболее ранних исследованиях анализ основан на расширенной аналогии Рейнольдса с передачей тепла, массы и импульса в развитом турбулентном потоке в трубе. Использование профиля распределения скорости и температуры в пограничном слое пре д ложено В.Д. Ранни [14]. Анализ подслоя учитывал влияние теплообмена на турбулентность. Аналитические методы определения коэффициентов теплоотдачи, предложенные в работах [15, 16], учитывают конвективный перенос тепла в камерах ЖРД и выполнены для прямолинейного турбулентного течения.
Конструктивные схемы ТНА ЖРД. Из анализа к онструктивных схем с овременных турбонасосных агрегатов ЖРД (рис. 1, 2) видно, что достаточно часто применяетс я схема одноблочного расположения проточных частей турбин и насосов (скомпонованы в един о м блоке). В проточных частях турбин реализуется температура продукто в сгорания порядка 900 °С, при использовании таких схемных решений высокие тепловые потоки от турбины к корпусу и к уплотнениям могут вызвать нарушение теплового режима, вследствие чего возможно термическое разрушение элементов узлов уплотнений. Наиболее важно корре к тное определение тепловых пот о ков для криогенных компонентов топлива при выбираемой одноблочной компоновке.
При проектировании проточных частей узлов и агрегатов ТНА ЖРД важно учитывать влияние теплообмена и как следствие – температуры поток а рабочего тела по длине проточного тракта, в связи с тем, что вязкость напрямую зависит от температуры и определяет потери и режим течения.
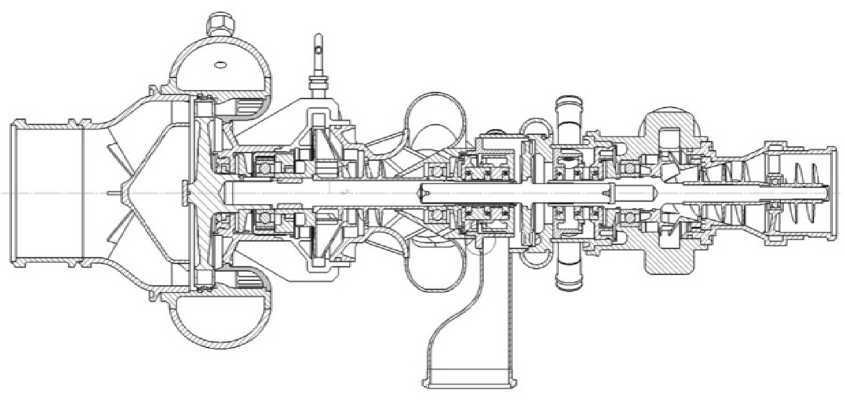
Рис. 1. ТНА ЖРД замкнутой схемы
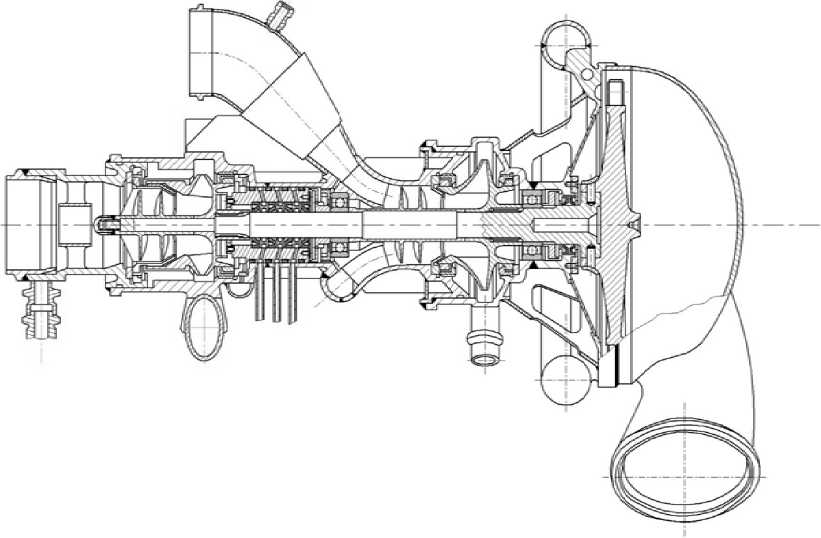
Рис. 2. ТНА ЖРД открытой схемы
В агрегатах подачи, особенно при использовании криогенных компонентов топлива, незначительный подогрев рабочего тела может привести к вскипанию компонентов и падению рабочих характеристик. С другой стороны, недостаточная (нерасчетная) температура компонента в проточной части для некоторых видов рабочих тел (например гелеобразных компонентов) приводит к повышенной вязкости и снижению КПД агрегата.
Объектом исследования вращательных течений являются конструктивные элементы проточных частей ТНА ЖРД: прежде всего полость между рабочим колесом и корпусом турбины и центробежного насоса, подводящие и отводящие аппараты, элементы ВГТ (вспомогательного гидравлического тракта), узлы контактных уплотнений.
Постановка задачи исследования. При исследовании задачи вращательных течений с теплообменом необходимо совместное решение уравнений движения и энергии в граничны х условиях проточных частей ТНА ЖРД с учетом теории пространственного пограничного слоя [17, 18].
Процессы теплоотдачи в энергетических установках во многом схожи, но при анализе и выводе уравнений теплообмена для граничных условий ЖРД существуют определенные отличия. Основные отличия заключаются в следующем: экстремально высокие значения тепл о вых потоков, температур и давлений, наличие высоких скоростей потоков, начальное турбул е нтное состояние потоков в активной зоне, рабочие тела могут находиться в газообразном и жидком состоянии, эффекты кривизны поверхности, наличие градиентов плотности и сжимаемости, нестационар-ность тепловых потоков и наличие неустойчивости п о токов в активной зоне теплообмена [19].
Модель температурного пограничного слоя с конвективной составляющей. Критерий Прандтля Pr в значительной мере влияет на теплообмен. Отметим, что для газов критерий Прандтля Pr < 1 (в том числе и для продуктов сгорания), для жидкостей критерий Прандтля Pr > 1 (компоненты топлива).
При Pr > 1 температурный пограничный слой м е ньше динамического (рис. 3). Тепловой поток от поверхности теплообмена может осуществляться за счет двух механизмов: теплопроводности или турбулентного переноса. При турбулентном течении скорость турбулентного переноса тепла и импульса значительно превышает скорость молекулярного переноса и поэтому молекулярным переносом можно вообще пренебречь. При к ритерии Прандтля, близком к единице или более высоком, преобладает турбулентный механизм переноса тепла, а молекулярным переносом можно пренебречь [20].
Так как коэффициенты турбулентного переноса значительно выше коэффициентов молекулярного переноса, в дифференциальных уравнениях движения и энергии можно пренебречь ки- нематическим коэффициентом вязкости и коэффициентом температуропроводности в отличие от коэффициентов турбулентного переноса импульса и тепла [20]. В случае больших чисел Рейнольдса теплопроводность жидкости не оказывает практического влияния на перенос тепла [17].
Основной механизм переноса тепла реализуется за счет переноса объема массы рабочего тела вдоль оси Y , вызванного изменением скорости в пограничном слое. Учитывая существующее подобие распределения температурного и скоростного профилей в пограничном слое (ПС) при критерии Прандтля, равном единице, когда безразмерные профили скорости и температуры идентичны, примем следующую модель распределения температурного и динамического ПС: распределение температурного ПС в границах толщины температурного слоя 8 t совпадает с профилем функции скорости ПС. Вне границы темпе-
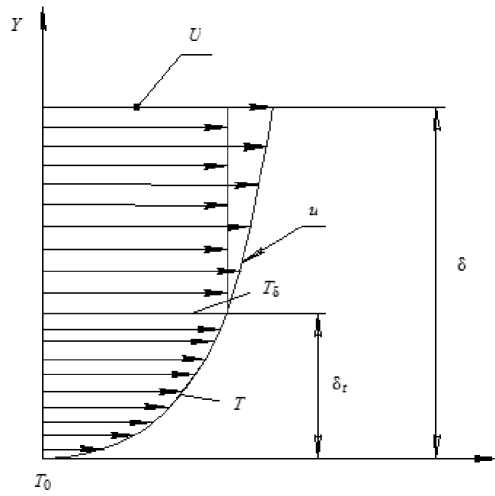
Рис. 3. Принятая модель температурного и динамического пограничных слоев
ратурного слоя 8 t температура потока не изменяется и равна температуре потока в ядре течения, но функция скорости продолжает изменяться до достижения толщины 8, далее принимает пара-
метры ядра.
Определим толщину потери энергии температурного ПС [21]:
5 е ** u 5 1
(
к
^^^^^^^в
5 T 0 У
dy .
На основе рассматриваемой модели температурного и динамического ПС выражение для толщины потери энергии разбиваем на два интеграла, соответствующих характерным участкам.
Границы интегрирования первого лежат от поверхности теплообмена до толщины температурно го ПС 8t, второго - от толщины температурного ПС 8t до толщины динамического 8.
Запишем выражение (1) в принятых границах интегрирования:
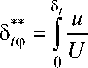
^^^^^^в
T - Т о ' T 5 - Т о У
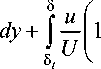
-
Т - Т о " Т 5 - Т о У
dy .
С применением уравнения (2) становится возможным определить вид закона теплообмена для случая Pr > 1. Для дальнейшего использования уравнение (2) необходимо проинтегрировать с учетом принятых законов распределения профиля скорости в ПС.
Распределение динамического ПС аппроксимируем степенной функцией вида u f y А m = .
U V5)
Как отмечалось, перенос тепла осуществляется за счет двух механизмов теплопроводности и переноса массы. У жидкостей теплопроводность на порядок больше, чем у газа, соответственно теплопроводностью пренебрегать не следует, тогда профиль распределения температурного ПС примем в следующем виде:
< 1 А
Т - Т о
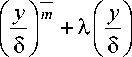
Т 5 - Т о
Запишем выражение для толщины потери энергии ПС:
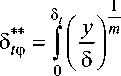
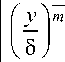
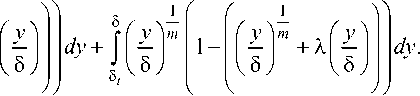
Учитывая, что в первом члене уравнения (3), исходя из принятой модели, в границах интегрирования профили распределения температуры и скорости совпадают, тогда для первого члена уравнения 8 t = 8.
При рассмотрении второго члена уравнения (3) и с учетом отсутствия градиента температу ры можно записать т. е.
т - Т о
т8
Т о
т8
т8
-
Т о
-
Т о
= 1,
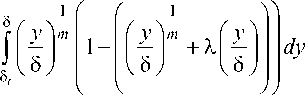
Тогда толщина потери энергии (3) при Pr > 1 в границах интегрирования от поверхности теплообмена до 8 t :
8ir
** f( y 1 m
8 1 d ■
(
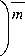
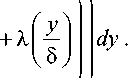
Толщина потери энергии из выражения (4) определится как
2 ( х ^
m8zf—Im -§f—Im + 28m2 + 28 + 58m-2X8t- 3Xm8t -28m2f—Im -Xm28t -38mf—V
**
8 1 ф =
1 (8 J (8 J 1 1 (8 J 1 (8 J
(J8( m +1)( m + 2)( 2 m +1)
Обозначим как x отношение толщины динамического ПС к толщине температурного ПС:
— = x .
Тогда m+1 ( XX 11
mx m 8 5 m - 3 mx m - x m + 2 m 2 - 2 m 2 x m - 2 X x - 3 X mx -X m 2 x + 2
8 = (J
-
1 ф ( m + 1 )( m + 2 )( 2 m + 1 )
Введем обозначение m+1 ( XX X1
X = mx m 5 m - 3 mx m - x m + 2 m 2 - 2 m 2 x m - 2 X x - 3 X mx - X m 2 x + 2
Для записи закона теплообмена в виде критерия Стантона необходимо определить производную температурного пограничного слоя на стенке (поверхности теплообмена). Данная производная не существует формально при m < 1, т. е. профиль не может быть использован в ламинарном подслое турбулентного профиля распределения параметров в ПС. Поэтому производную температурного пограничного слоя на стенке определяем, исходя из двухслойной модели турбулентности с ламинарным подслоем. Тогда производная температурного пограничного слоя на стенке определится как д ду
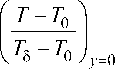
U ( а Л v 1 m +1 a 2 v ( U 8 1 J
Определим толщину динамического ПС из уравнения для толщины потери энергии температурного ПС (5):
5 = 5 ** ( m + 1 )( m + 2 )( 2 m + 1 )
X
.
Закон теплообмена. Учтем выражение для закона теплообмена и запишем выражение для безразмерного коэффициента теплоотдачи в виде критерия Стантона для турбулентного течения:
St =
X U
a 2 v
m + 1
pCpU a2v U5,
.
Принимая во внимание параметр отношения толщин динамического и температурного по- граничных слоев x = —, а также выражение толщины динамического ПС и выражение для зако на теплообмена (7), получим m+1
St =
■ p cpum+1 ka
X
m - 1
.m-1v 2 (m +1)(m + 2)(2m +1)
** \ .
1 m + 1
5 t ф )
.
Для практической реализации закона теплообмена необходимо определить значение коэффициента ламинарного подслоя aл, которое находим из условия смыкания ламинарного подслоя с турбулентным профилем [21], с учетом степени турбулентности, получим выражение для определения коэффициента ламинарного подслоя турбулентного профиля распределения температурного ПС для принятой модели:
a л =12,559
** 0,167 —
**
k5 t Ф J
12,5496 Pr 0,0557 .
Интегральное соотношение уравнения энергии. Уравнение энергии пространственного пограничного слоя (ППС) с учетом полученного выражения для закона теплообмена (8) преобразуется к виду
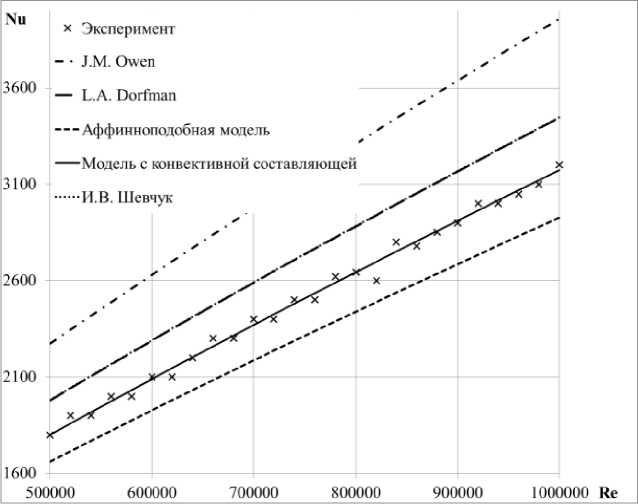
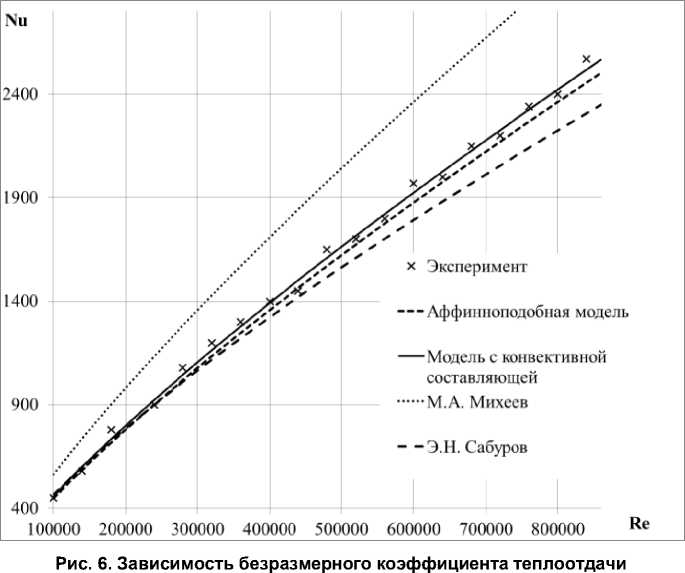
1 д / ** \ 1 д / ** \ 15/ Hф дф(tф)Hv dv(tv) HфHv • ■ p CpUm+1 ka' X дHv .** 1 -------5/(o +-- дф tф Hф Hv A m+1 m-1 .m-1v 2 (m +1)(m + 2)(2m +1) • dHф ** _ dv tv тфо (1 + 82) ft 1 m+1 51Ф ) p Cp (T5-To)" Принимая относительную характерную толщину ** 1. J X** , 8 51Ф интегральное соотношение уравнения энергии (9) примет вид 1 d / „**\ J d 151 ф ) + Hф дф^ ф' Hv dv +-- Hф Hv 1 dH • дф ^5: J ** J 1 tф +и и H ф H v • dHф _ дv tф m+1 ■ 2 p CpUm+1ka X m-1 . m -1v (m +1)( m + 2)(2 m +1) ft I m+1 и t ф ) тфо (1 + 82) P Cp (T5-To)’ S Учитывая, что реализуется прямолинейное равномерное течение, получим: — = 0, H^ = Нф, д— — ф дH, дH„ —— = —— = 0 , тогда интегральное соотношение уравнения энергии (11) преобразуется к виду дф д— m+1 д** _ dv6tф X р CpUm+1^a' m -1 .m-1v 2(m +1)(m + 2)(2m +1) X | m+1 u t V ) р Cp (т5- To У При рассмотрении вращательного течения, реализующегося в полостях ТНА ЖРД, линия тока представляет собой кольцевую линию. Выполним запись уравнения (12) в цилиндрических координатах, учитывая, что в случае осесимметричного течения при ε = const выполняются соот- дH ф дR ношения ф = a, v = R , Hm = R , —- = — ф дф дR = 1, Hv= 1, ^H^ = o, T = 0: дф дф A m+1 д ** J s—6,m +0, дR tv R дR tф ' 2 р CpUm+1^a' X m-1 ,m-1v 2(m +1)(m + 2)(2m +1) x X2 ft 1 m+1 u t ф ) тфо (1 + s2) р Cp (To- To)" Таким образом, получены выражения интегрального соотношения уравнения энергии температурного пограничного слоя прямолинейного равномерного и вращательного течений с учетом степенного закона распределения параметров температурного и динамического пограничных слоев и принятой модели теплообмена для случая Pr > 1. Локальный коэффициент теплоотдачи. Рассмотрим далее локальную теплоотдачу для практически важных случаев, реализующихся в элементах проточных частей ТНА ЖРД при Pr > 1 и принятого степенного закона распределения параметров скорости и температуры в ПС. Характерными течениями являются течения в трактах подачи жидких компонентов топлива ракетного двигателя. Последовательно рассмотрим следующие характерные течения: прямолинейное равномерное течение потока, вращательное течение потока по закону твердого тела (реализуется в полостях между ротором и статором) и вращательное течение потока по закону свободного вихря (подводящие и отводящие устройства). Рассматривая прямолинейное равномерное течение и учитывая, что пренебрегаем диссипативным членом в интегральном соотношении уравнения энергии (12), запишем m+1 д** _ дф6tф ' р CpUm+1^a' X m-1 .m-1v 2(m +1)(m + 2)(2m +1) • ft I m+1 61V ) . Разделим переменные и проинтегрируем (14) от нуля до текущего значения переменных: ** 6tф Хф р CpUm+1 m+1 3+m 2 m+2 (m+1)(3+m) m+1 ( 3 + m A 3+m m-1 am-1v 2(m +1)(m + 2)(2m +1) • m +1 . С учетом выражения закона теплоотдачи (8) и выражения для толщины потери энергии (15) запишем, а также проведя преобразования выражения (15), с учетом критериев Прандтля И C Pr = p X I PUФ I и Рейнольдса Re =----I, получим выражение для определения локального коэф- V И У фициента теплоотдачи в виде критерия Стантона прямолинейного равномерного течения при степенном профиле распределения эпюры скорости и температуры при Pr > 1: St = m+1 Pr3+mV X am 1 (m + 2)( m + 3)( 2 m +1) Re 3+m . Рассмотрим вращательное течение, реализующееся в проточных частях ТНА ЖРД. Аналогично, как и при прямолинейном равномерном течении потока, пренебрегая диссипативным членом и учитывая, что реализуется вращательное течение по закону твердого тела, характерной особенностью которого является распределение окружной составляющей скорости по радиусу — = ы = const, уравнение (13) преобразуется к виду R ** 5 „** 5tm —5, + dR tmR X J ер Cp го m+1 m-1 am-1v 2 (m +1)(m + 2)(2m +1) m +1 .1 = 0. Dm+1 (ft** \m+1 R (ut m) Из уравнения (17) определим выражение для толщины потери энергии температурного ПС для вращательного течения по закону твердого тела: m+3 m+1 ** 5 t m = \ X J ер Cp го m+1 X am 1v 2 (m +1)(m + 2)(2m +1) m+1 m-1 (m + 3) Rm+1 . С учетом выражения закона теплообмена (8) критерий Стантона для вращательного течения по закону твердого тела степенного профиля распределения температурного пограничного слоя и Pr > 1 примет вид St = 1 I____________2 JeX____________' — lam-1 (m + 2) (m + 3)(2 m + 1)Re„ Dr-m+3 V л\ /V /V У ЮУ Рассмотрим вращательное течение, которое осуществляется по закону свободного вихря. Закон распределения профиля скорости ядра потока по радиусу примет вид UR = C = const. Данное течение характерно для следующих элементов: подводящего и отводящего устройств насосов подачи компонентов топлива, камер закрутки и т. д. При рассмотрении вращательного течения по закону свободного вихря интегральное соотношение уравнения энергии (13) примет вид ** ** d 5* m+8^ -dR R m+1 X J е CpCm+1 X Rm+1 m-1 am-1v 2 (m +1)(m + 2)(2m +1) = 0. Из уравнения (20) определим выражение для толщины потери энергии температурного ПС вращательного течения по закону свободного вихря для степенного закона распределения профилей пограничного слоя при Pr > 1: ** ° t ф = X J £ CpCm1 X A m+1 m-1 .am-1v 2 (m +1)(m + 2)(2m + 1); m +1 /2 m+3 m +1 m+3 • R. Подставив выражение для определения толщины потери энергии (21) в выражение закона теплообмена (8), получим локальный коэффициент теплоотдачи в виде критерия Стантона для вращательного течения по закону свободного вихря для случая Pr > 1: e 1 2 J £X St =------Г -----i . — am- (m +1)(m + 2)(2m + 1)Rem prm+3 V л v На рис. 4 показано влияние критерия Прандтля на трение и теплообмен по данным различных исследований [22]. В области значений чисел Прандтля Pr > 1 полученные теоретические зависимости для безразмерных коэффициентов теплоотдачи в виде критериев Стантона, с учетом интегрального соотношения уравнения энергии, хорошо совпадают с зависимостями других авторов. Cf представляет коэффициент трения. Рис. 4. Сравнение различных теорий аналогии между трением и теплообменом в турбулентных потоках при Re = 107 Коэффициент теплоотдачи в виде критерия Нуссельта представляет произведение критериев Стантона, Рейнольдса и Прандтля Nu = St RePr. На рис. 5 приведены результаты экспериментальных и теоретических зависимостей для турбулентного вращательного течения по закону твердого тела. Из графической зависимости рис. 5 видно, что результаты теоретических исследований, полученных с использованием модели с конвективной составляющей, наилучшим образом совпадают с экспериментальными данными и не превышают 3 %. Теоретические зависимости, полученные И.В. Шевчуком [23] и L.A. Dorfman [24], практически совпадают и отличаются на 0,05 %, с данными по теоретической зависимости с использованием модели с конвективной составляющей расходятся на 10 %. Зависимость, полученная J.M. Owen [25], с теоретической зависимостью модели с конвективной составляющей отличаются на 26 %. Рис. 5. Зависимость безразмерного коэффициента теплоотдачи турбулентного вращательного течения по закону твердого тела при Pr = 4,341 турбулентного вращательного течения по закону свободного вихря при Pr = 4,341 На рис. 6 приведены результаты экспериментальных и теоретических зависимостей вращательного течения по закону свободного вихря. Из графика рис. 6 видно, что наилучшее схождение результатов экспериментальных данных и теоретических зависимостей дает также зависимость, полученная с использованием модели распределения динамического и температурного ПС с конвективной составляющей, расхождение результатов не превышает 2,5 %. Полученные теоретические зависимости и зависимости других авторов находятся в едином диапазоне и пригодны для инженерных расчетов при проектировании ТНА. Необходимо отметить, что на безразмерный коэффициент теплоотдачи в виде критерия Нуссельта существенно влияют граничные условия течения и теплообмена, такие как скорость, вязкость, плотность и градиент температур рабочего тела и поверхности теплообмена. Выводы. При интегрировании уравнения энергии в граничных условиях толщины температурного пространственного пограничного слоя получено уравнение для интегрального соотношения, необходимое для учета процессов теплоотдачи. Полученное выражение позволяет учитывать теплоотдачу на поверхности любой формы. С учетом интегрального соотношения определены и записаны выражения для толщин потери энергии. В свою очередь толщины потери энергии температурного пространственного пограничного слоя необходимы для определения локальных коэффициентов теплоотдачи для характерных случаев течения с учетом теплообмена. С использованием аналитического подхода определены уравнения для расчета локальных коэффициентов теплоотдачи в виде критериев Стантона для наиболее важных случаев, реализующихся при течении в полостях вращения ТНА ЖРД. Получены локальные коэффициенты теплоотдачи при прямолинейном течении, вращательных течениях, реализующихся в полостях между рабочим колесом и корпусом турбины и центробежного насоса (течение по закону твердого тела), в подводящих и отводящих аппаратах (течение по закону свободного вихря). Полученные аналитические выражения для локальных коэффициентов теплоотдачи хорошо согласуются с результатами исследований других авторов и имеют практическое применение при расчете характеристик тракта ТНА ЖРД.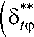
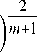
Список литературы Определение локального коэффициента теплоотдачи с использованием модели температурного пограничного слоя с конвективной составляющей в полостях вращения ТНА ЖРД
- Aerodynamic design method of micro-scale radial turbines considering the effect of wall heat transfer / Z. Li, Z. Zou, L. Yao, C. Fu, L. Bian, W. Zhang // Applied Thermal Engineering. - 2018. - Vol. 138. - P. 94-109. DOI: 10.1016/j.applthermaleng.2018.04.051
- Chen, Y. Experimental Study on the Conjugate Heat Transfer of Double-wall Turbine Blade Components with/without Pins / Y. Chen, H. Wei, Y.Q. Zu // Thermal Science and Engineering Progress. - 2018. - Vol. 8. - P. 448-456. DOI: 10.1016/j.tsep.2018.09.010
- Mobtil, M. Experimental study of inverse identification of unsteady heat transfer coefficient in a fin and tube heat exchanger assembly / M. Mobtil, D. Bougeard, S. Russeil // International Journal of Heat and Mass Transfer. - 2018. - Vol. 125. - P. 17-31. DOI: 10.1016/j.ijheatmasstransfer.2018.04.028
- Heat transfer in turbocharger turbines under steady, pulsating and transient conditions / R.D. Burke, C.R.M. Vagg, D. Chalet, P. Chesse // International Journal of Heat and Fluid Flow. - 2015. - Vol. 52. -P. 185-197. DOI: 10.1016/j.ijheatfluidflow.2015.01.004
- Fadl, M. Full conjugate heat transfer modelling for steam turbines in transient operations / M. Fadl, P. Stein, L. He // International Journal of Thermal Sciences. - 2018. - Vol. 124. - P. 240-250. DOI: 10.1016/j.ijthermalsci.2017.10.025
- Winkler, S. Flow structure and surface heat transfer from a turbine component endwall contoured using the ice formation method / S. Winkler, B. Weigand, P. Ligrani // International Journal of Heat and Mass Transfer - 2018. - Vol. 120. - P. 895-908.
- DOI: 10.1016/j.ijheatmasstransfer.2017.12.028
- Effects of a pocket cavity on heat transfer and flow characteristics of the endwall with a bluff body in a gas turbine engine / J. Liu, S. Hussain, L. Wang, G. Xie, B. Sundén // Applied Thermal Engineering. - 2018. - Vol. 143. - P. 935-946.
- DOI: 10.1016/j.applthermaleng.2018.08.020
- Park, J.S. Heat and mass transfer characteristics on the first-stage gas turbine blade under unsteady wake flow / J.S. Park, W. Choi // International Journal of Thermal Sciences. - 2019. - Vol. 138. - P. 314-321.
- DOI: 10.1016/j.ijthermalsci.2019.01.008
- Effect of the wake on the heat transfer of a turbine blade end wall according to relative position of the cylindrical rod / S.M. Choi, J. Kim, M. Bang et al. // International Communications in Heat and Mass Transfer. - 2018. - Vol. 94. - P. 61-70.
- DOI: 10.1016/j.icheatmasstransfer.2018.03.011
- A 3D analytical model for orthogonal blade-vortex interaction noise / M.E. Quaglia, T. Léonard, S. Moreau, M. Roger // Journal of Sound and Vibration. - 2017. - Vol. 399. - P. 104-123.
- DOI: 10.1016/j.jsv.2017.03.023
- Shaeri, M.R. Analytical heat transfer model for laterally perforated-finned heat sinks / M.R. Shaeri, R.W. Bonner // International Journal of Heat and Mass Transfer. - 2019. - Vol. 131. - P. 1164-1173.
- DOI: 10.1016/j.ijheatmasstransfer.2018.11.138
- Analytical solution to heat transfer in compressible laminar flow in a flat minichannel / C. Bao, Z. Jiang, X. Zhang, J.T.S. Irvine // International Journal of Heat and Mass Transfer. - 2018. - Vol. 127. - P. 975-988.
- DOI: 10.1016/j.ijheatmasstransfer.2018.08.084
- Verstraete, D. Impact of heat transfer on the performance of micro gas turbines / D. Verstraete, C. Bowkett // Applied Energy. - 2015. - Vol. 138. - P. 445-449.
- DOI: 10.1016/j.apenergy.2014.10.075
- Rannie, W.D. Heat transfer in turbulent shear flow / W.D. Rannie // J. Aeronaut. Sci. - 1956. - Vol. 23. - P. 485-489.
- Stechman, R.C. Design criteria for film cooling for small liquid-propellant rocket engines / R.C. Stechman, J. Oberstone, J.C. Howell // J. Spacecr. Rocket. - 1969. - Vol. 6. - P. 97-102.
- Bartz, D.R. A simple equation for rapid estimation of rocket nozzle convective heat transfer coefficients / D.R. Bartz // Jet. Propuls. ARS J. - 1957. - Vol. 27. - P. 49-51.
- Романенко, П.Н. Тепломассообмен и трение при градиентном течении жидкостей / П.Н. Романенко. - М.: Энергия, 1971. - 568 с.
- Шлихтинг, Г. Теория пограничного слоя / Г. Шлихтинг. - М.: Наука, 1974. - 712 с.
- Shine, S.R. Review on film cooling of liquid rocket engines / S.R. Shine, S.S. Nidhi // Propulsion and Power Research. - 2018. - Vol. 7 (1). - P. 1-18.
- DOI: 10.1016/j.jppr.2018.01.004
- Кейс, В.М. Конвективный тепло- и массообмен: пер. с англ. / В.М. Кейс. - М.: Энергия, 1972. - 448 с.
- Кишкин, А.А. Локальная теплоотдача в граничных условиях турбомашин / А.А. Кишкин, А.А. Зуев, В.П. Леонов // Известия высших учебных заведений. Машиностроение. - 2015. - № 1 (658). - С. 3-10.
- Chapman, D.R. Measurements of turbulent skin friction on cylinders in axial flow at subsonic and supersonic velocities / D.R. Chapman, R.H. Kester // JAS. - 1953. - Vol. 20. - P. 441-448.
- Shevchuk, I.V. Convective Heat and Mass Transfer in Rotating Disk Systems / I.V. Shevchuk. - Springer, 2009. - 235 p.
- Дорфман, Л.А. Гидродинамическое сопротивление и теплоотдача вращающихся тел / Л.А. Дорфман. - М.: Физматгиз, 1960. - 260 с.
- Owen, J.M. Flow and heat transfer in rotating disc systems. Rotor-stator systems / J.M. Owen, R.H. Rogers. - Taunton: Research Studies Press, 1989. - 302 p.


