Определение массогеометрических характеристик элементов баллистических летательных аппаратов
Автор: Фдоров Виктор Борисович, Юрин Иван Фдорович
Рубрика: Расчет и конструирование
Статья в выпуске: 10 (186), 2010 года.
Бесплатный доступ
Предложен подход к определению маесогеометрических характеристик элементов баллистического летательного аппарата. Показано, что для определения всех массогеометрических характеристик двух элементов необходимы максимум три цикла измерения маесогеометричееких характеристик баллистического летательного аппарата в целом. Поставлена задача вычисления такой пространственной ориентации элементов баллистического летательного аппарата, которая удовлетворяет требованиям конструкторской документации к массогеометрическим характеристикам всего аппарата. Предложен подход к ее решению.
Баллистический летательный аппарат, массогеометрические характеристики, тензор инерции, центр масс
Короткий адрес: https://sciup.org/147151481
IDR: 147151481 | УДК: 681.518.5
Текст научной статьи Определение массогеометрических характеристик элементов баллистических летательных аппаратов
Существует способ изменения (коррекции) массогеометрических характеристик объектов путем перераспределения массы. Под массогеометрическими характеристиками (МГХ) понимаем три осевых и три центробежных момента инерции, массу, координаты центра масс. Применительно к баллистическим летательным аппаратам (БЛА) данный способ изменения МГХ может быть реализован за счет перемещения внутри БЛА какого-либо одного массивного тела (элемента) с собственным эллипсоидом инерции, соизмеримым с эллипсоидом инерции всего БЛА (см. рисунок). В качестве такого перемещаемого тела может выступать полезный груз БЛА.
Для осуществления коррекции МГХ БЛА подобным способом необходимо решить две задачи:
-
1. Определение МГХ элементов (полезного груза и корпуса) БЛА.
-
2. Определение пространственной ориентации элементов БЛА, удовлетворяющей нормируемым в конструкторской документации номинальным параметрам МГХ всего БЛА.
Вопросы контроля МГХ для баллистических аппаратов с постоянными МГХ подробно рассмотрены в работах [1-4]. Поэтому предлагается, осуществлять контроль МГХ БЛА с изменяемыми МГХ с использованием способов определения МГХ БЛА с постоянными МГХ. Предлагаемый подход по сути своей является параметрической идентификацией системы и заключается в том, что для сбора информации о МГХ элементов нужно провести несколько циклов полного определения МГХ для БЛА с зафиксированными элементами, при этом на каждом цикле измерения в положение элементов вносится изменение. БЛА с зафиксированными элементами предлагается рассматривать как твердое тело с соответствующими МГХ. По завершению измерений производится вычисление значений МГХ элементов по предложенной авторами в данной статье методике.
Подобная задача в похожей постановке решалась Ивановым И.И., Тверским М.М. [2, с. 168— 175] в контексте получения дополнительной информации на балансировочном стенде о теле мето- дом последовательного вращения вокруг трех осей. Методика Иванова и Тверского позволяет определять моменты инерции J^ Jw J^ и продольную координату центра масс (ЦМ) х перемещаемого элемента (в текущей постановке задачи это полезный груз, перемещаемым элементом был сам БЛА, а вместо корпуса выступала дополнительная оснастка). Авторы данной статьи используют подобный подход при несколько иной и более общей постановке задачи.
Полагаем, что на измерительном стенде за один цикл измерений можно определить координаты центра масс БЛА и тензор инерции БЛА в конструкторской системе координат, масса БЛА определяется заранее. Кроме того, заранее возможно определить массу корпуса и тензор инерции корпуса БЛА, массу перемещаемого груза. Определение же тензора инерции перемещаемого груза, в виду отсутствия у него удобных для базирования поверхностей, в условиях производства будет затруднено. Считаем, что взаимное положение элементов БЛА может устанавливаться с большой точностью.
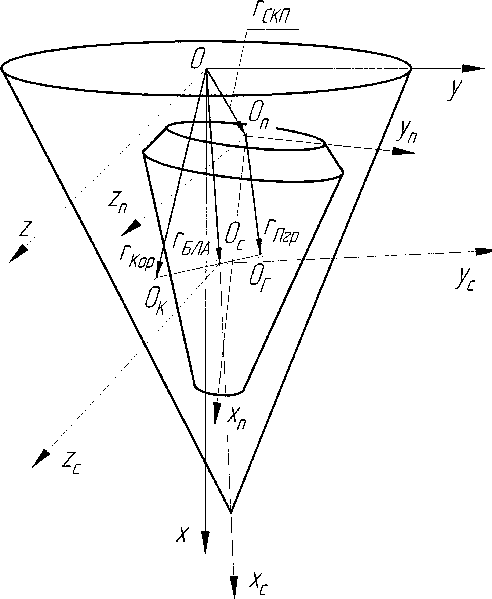
Баллистический летательный аппарат с изменяемыми массогеометрическими характеристиками
Рассмотрим задачу определения МГХ элементов БЛА в трех различных случаях:
-
1. Производится необходимое число циклов измерения полного комплекса МГХ БЛА.
-
2. Производится необходимое число циклов измерения полного комплекса МГХ БЛА и заранее проведены измерения массы перемещаемого груза (либо массы корпуса).
-
3. Производится необходимое число циклов измерения полного комплекса МГХ БЛА, заранее проведены измерения тензора инерции корпуса, положения центра масс корпуса и массы корпуса.
Введем системы координат:
-
• Ox^z - конструкторская система координат (КСК), связанная с корпусом БЛА. Ось Ох в общем случае не параллельна оси приведения, а начало координат в общем случае не совпадает с центром масс корпуса или БЛА;
-
• Ок-ХкУк^к - система координат, оси которой параллельны осям Ox^z, начало координат совпадает с центром масс корпуса БЛА;
-
• ОцХпУп^п - конструкторская система координат, связанная с полезным грузом. Начало координат Оп в общем случае не совпадает с центром масс полезного груза;
Расчет и конструирование
-
• Ог-^гУг^г - система координат, оси которой параллельны осям Оп*пУп£п, начало координат совпадает с центром масс полезного груза;
-
• Ос^сУс^с ~ система координат, ось Ос^с которой связана с осью приведения, две другие оси дополняют систему до правой тройки, начало координат Ос совпадает с номинальным положением ЦМ БЛА.
Положение начала Оп СК Оп^пУп^п в СК Oxyz определяется вектором гскп .
Взаимное положение элементов БЛА (корпуса и полезного груза) определяется матрицей поворота А1 и вектором переноса гскп и является преобразованием из СК Оп^пуп^п в СК Oxyz.
Преобразование из Oxyz в ОсхсУс£с определяется матрицей поворота А2 и вектором переноса 'бла •
Положение координаты ЦМ БЛА в целом и положение ЦМ корпуса задается соответственно векторами гБЛА, гкор в Oxyz, положение координаты центра масс полезного груза задастся вектором гпгр в Оп*пУп2п (см. рисунок). -
Из условия равенства статических моментов элементов БЛА можно записать выражения:
^кор 'кор ~*~ ^п.гр ^^ 'п.гр "*~ ^п.гр 'СКП “ 'БЛА ^БЛА ’ (1)
где Мкор - масса корпуса БЛА; Мп.гр - масса перемещаемого полезного груза БЛА; МБЛА - масса БЛА в целом:
^БЛА ” ^кор ^п.гр ' (2)
Положение координат полезного груза исходя из нормируемых координат ЦМ БЛА и известных координатах ЦМ корпуса:
(А1гп.гр + ГСКП /
^п.гр
В равенстве (1) МБЛА - величина известная и постоянная, гскп - величина известная и варьируемая, А1 - матрица поворота известная и варьируемая, гБЛА - величина известная и измеряемая, гкор, гп гр, Мкор, Мп гр - искомые величины.
Проводя несколько измерений гБЛА на стенде и при этом каждый раз изменяя взаимное расположение элементов БЛА, определяемое матрицей поворота А1 и вектором переноса гскп , возможно определить искомые величины. Полученные или измененные в процессе каждого измерения величины будем обозначать нижним индексом, соответствующим номеру измерения ( 'блар ^1р гскт и Т-Д-)- Тогда, после трех измерений можно записать выражения:
^кор 'кор ~^" ^п.гр А1^ Гп pg + Мп рр ?скп1 — 'бЛА1 ^БЛА ’
^кор 'кор + ^п.гр AI2 гр + ^п.гр 'СКП2 ” 'БЛА 2 ^БЛА ’ (4)
^кор 'кор ~*~ ^п.гр ^^3 'п.гр "^ ^п.гр 'СКПЗ ” 'ВЛАЗ ^БЛА"
Вычитанием второго выражения из первого (4) и третьего выражения из первого (4) получается:
^п.гр(А1] ”А12)гпгр +Мпгр^Гскп1 -Гскп2) = МБла(гблА1 — ^БЛАг)’
^п.гр (All - AI3 ) Гп гр + Мп гр (гскш - ГСКПЗ ) = ^БЛА (ГБЛА1 ~ ГБЛАЗ )■
Отсюда выражается гп ^
_ (А1, А12) МБЛА / \ , .т/ п.гр - ” ( ГБЛА1 - ГБЛА 2 ) - ( All - А12 ) ( ГСКП1
ГСКП2 )’
^п.гр
_(Ali А13) МБЛА, _ х т/ _ \ п.гр” м ('бла1 гБЛАЗ/ КА11 А13/ (гСКП1 гскпз/-
Подстановкой гп ^ в одно из выражений (4) получается:
^кор гкор + (Е - Alx A1J )мБЛА (гБЛА1 - гБЛА2) -
”^п.гр (е™ A^AlJ )(гскш -гСКП2) + Мпгр гскп1 = гБЛА1МБЛА,
^кор гкор + (Е - Alx A1J )мБЛА (гБЛА1 - гБЛАЗ) -
-
-Л^Пгр(Е-A^AlJ)(гСКП1 -гскпз) + Мплр гСКП1 = гБЛА1МБЛА.
Вычитанием одно из другого получается:
^п.гр ((AliAl2 )(гСКП2 -r^n^-^A^AlJ ^гскпз -гскп1 j + rCKn3 “rCKn2) =
“ ^БЛА ((^1 ^2 )(ГБЛА2 “гБЛА1)”(^11^1з )(ГБЛАЗ “ ГБЛА1) + ГБЛАЗ ”ГБЛА2)'
Из равенства (6) определяется Мп ^ :
^п.гр =^БЛа((А11А12 ^ГСКП2 -Гскш j-^A^AlJ ^Гскпз -^СКП1) + ГСКПЗ “ГСКП2 j х AllA1J)(гБЛА2 -/бда1)”(а11А1^)^ -гбла1) +гблаз -гбла2
Подстановкой полученного значения Мптр в (5) вычисляется гп ^ , аналогично вычисляется гкор из (4) с учетом (2).
Таким образом, для вычисления координат центров масс элементов БЛА и значения масс элементов БЛА, при известной массе БЛА в целом, а также при возможности точной взаимной ориентации элементов БЛА (или возможности точного определения взаимного положения элементов БЛА) достаточно трех циклов измерений положения координат центра масс БЛА с различной взаимной ориентацией элементов БЛА в каждом из циклов измерений. В случае если массы элементов БЛА определены заранее, то достаточно только двух циклов измерений координат центра масс БЛА, если же известно и положение центра масс одного из элементов, то достаточно одного цикла измерения координат центра масс БЛА.
Выражение для тензора инерции БЛА в Ох^г с учетом теоремы Гюйгенса-Штейнера запишется следующим образом:
^БЛА ~ Jrop ^" ^^ [ ^п.гр ^^п.гр f (^-l^n.rp + ^СКП ) (^-1 Гп гр + Г^кп )Е —
Т (7)
4АКгр +гСКп)(А1гп.п, +гСКп) -^rp^rpE + r^rJ 1U1.
где JKOp - тензор инерции корпуса в СК Ox^r, Jn ^ - тензор инерции перемещаемого груза в СК Оп^пУп^п; Е - единичная матрица размерностью 3x3.
Как и ранее в нижнем индексе обозначается номер проводимого цикла измерений. Тогда для каждого цикла измерений:
^БЛАА: — ^кор "^ ^^ ^п.гр^^А: "^ ^п.гр ^^ f (^^ ^п.гр ~*~ ^СКП^ ) (^^^ ^п.гр "*" ^СКП^ )Е “ т т т ) (8)
— (^^ ^п.гр "^ ^СКП £ ) ( ^^А: ^п.гр "^ ^СКП к ) ^.гр ^п.гр Е + ^п.гр ^п.гр J *
Вычитанием выражения (8) для второго цикла измерения из выражения для первого цикла измерений получается:
Расчет и конструирование
Al| JnrpAlj A12JnrpA12 J бы Jbb2
+^п.гр ’ ^1^ ^(А12 Гп гр + ГСКП2 ) (А12 Гп гр + гСКП2 )В -
-
~(^-^2 ^п.гр ^СКП2 )(^1з ^п.гр + ^СКП2 ) ~ ^плр ^пдр ® ^плр ^п.тр ^^^2 (9)
-
-Al^ ^Alj гп гр + гСКП1) (А^ гп гр + гСКП1 )Е -
- ""(All ^п.гр ~^" ^СКП2 )(^^1 ^п.гр ^СКП2 ) ^п.гр ^п.гр ® + ^п.гр ^п.гр ^j Alj
При переходе Jn ^ посредством матрицы-оператора линейного преобразования S из одного векторного пространства в другое STJn rpS, будет получена матрица J п ^ подобная Jn ^ с элементами вида:
где Ci - константа, составленная элементами матрицы S.
Тогда равенство (9) представляет собой квадратную систему из шести линейных уравнений, которая в общем случае нс будет совместной:
где i = 1...6.
Для нахождения компонентов тензора Jn ^ воспользуемся подходом Иванова И.И., Тверского М.М., для этого будем осуществлять ориентацию полезного груза на каждом цикле измерений особым образом.
-
• На первом цикле измерения (8) полезный груз ориентируется таким образом, что оси СК ОпХпУп^п параллельны осям Oxyz, матрица ориентации А1 является единичной, назовем это положение «начальным».
-
• На втором цикле измерений (8) полезный груз повернут из начального положения относительно оси ОцУп на определенный угол.
-
• На третьем цикле измерений (8) полезный груз повернут из начального положения относительно оси Оп£п на определенный угол (для удобства построения выражений угол предлагается использовать такой же, как и на втором цикле).
Тогда, приводя (8) для каждого цикла измерений к виду (11) и комбинируя определенным образом уравнения, можно выделить уравнения, из которых определятся все компоненты тензора Jn ^ :
-
^ 13 2 Аьгрхх (^33 2 — 1) ^n.rpzz ^13 2 ^33 2 ^n.rpxz ” ^n.rp2zz ^n.rplzz’
^12 2^212 + ^112^22 2 ~1)^п.грху +(a21 2 a32 2 + a22 2 a31 2)^n.rpxz =^n.rpl^ ”^n.ip2^’
(^113 — ^)^n.rpxx+^21 3 *^n.rpyj ~ 2tin 3 U21 3 ^n.rpxy “ ^n.rp2xx—^n.rplxx’ (12)
-
^ 12 3 ^n.rpxx + ^22 3 1) ^n.rpyp ~ ^12 3 ^22 3 ^n.rpxy “' ^n.rp2jj ^n.rplyj’
(a13 3a31 +a113a33 3 -l)^n.rpxz +(a213a33 3 + a23 3 a31 3 )^n.rpzy =^n.rplxz ~^n.rp3xz ’
(a13 3^32 3 + ^12 3 ^33 3 )^n.rpxz ^^a23 3 a32 3 + a22 3 a33 3 -l)^n.rpzy =^n.rplzy ”^n.rp3zy’ где ац k - компоненты матрицы Al на к цикле измерений, bn rpkij - ij компонент к цикла измерений результирующей матрицы В^ выражения:
^БЛАЛ ^плр (^^£ ^плр ^СКП£ ) (^^£ ^пл^ ^СКМ )®
^-Ц: ^п.гр "^ ^СКП£ Д^-Ц; ^.гр + ^СКПА: ) ^тр ^плр ^ ^ ^п.гр ^п.гр 1м^^'
После определения элементов тензора инерции Jn ^, из равенства (7) вычисляется тензор инерции JKop.
Если JKop был определен заранее, то Jn рр можно сразу вычислить из равенства (7).
Таким образом, для определения тензоров инерции элементов БЛА достаточно трех циклов измерений тензора инерции БЛА, при условии, что ранее были определены их массы и координаты центров масс. В случае если известен тензор инерции корпуса БЛА, то тензор инерции перемещаемого груза определяется за один цикл измерений.
Рассмотрим задачу определения пространственной ориентации элементов БЛА, удовлетворяющей нормируемым в конструкторской документации номинальным параметрам МГХ всего БЛА.
МГХ БЛА регулируются конструкторской документацией (КД) определенным образом, причем, нормируемые параметры не равны по своей значимости и влиянию на функциональность БЛА [4, с. 67-69]. Наибольшее влияние на функциональность БЛА оказывают отклонения положения центра масс и угловое отклонение главной центральной оси инерции (ГЦОИ) от нормируемого КД положения. В КД положение ЦМ и ГЦОИ БЛА, как правило, связывают с некоторой осью (далее будем называть «осью приведения»), которая в свою очередь каким-либо образом определяется параметрами наружной поверхности.
Под нормируемыми номинальными параметрами в данном случае подразумеваются три координаты центра масс в конструкторской системе координат, определяемые вектором гБЛА , и ось приведения, параллельно которой должна располагаться одна из главных центральных осей инерции БЛА. Пространственное положение оси приведения в КСК определяется матрицей поворота А2.
Полагаем, что определены все МГХ элементов БЛА (корпуса и полезного груза), а именно масса, положение ЦМ, тензор инерции.
Как отмечалось ранее, взаимное расположение элементов БЛА, а именно корпуса и полезного груза определяется вектором гскп и матрицей поворота А1.
Выражение для вычисления тензора инерции БЛА в СК Ос-^сУс^с при известных тензорах инерции его элементов и взаимном расположении элементов с учетом теоремы Гюйгенса-Штейнера можно записать аналогично (7) в следующем виде:
^бла “ А2Т JejiaA2 -
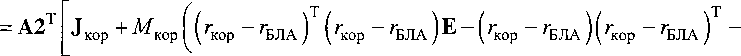
^кор ^кор ® ^кор ^кор )^ ^^ + А2 Al Jn рр + М п рр ^П-Гр ^П Гр ^п гр Гп рр Е +
+(А1гпгр + гскп -гбла) ^А1гпгр + гскп -гбла)Е-
С учетом (1) и положив:
Расчет и конструирование
Гкор 'БЛА ) ('кор 'БЛА ) ^ ('кор 'БЛА ) ('кор 'БЛА ) ’ можно записать:
^БЛА — А2 Г *Ьор 4^кор (^ — 'кор 'кор ® 'кор 'кор
+А1Т J
+ М
ПГр 1 ^^п.Гр
М. \
А1
А2.
Выражение (15) можно записать в виде:
1БЛА = А2Т (N + А1ТМ Al) А2,
где N, М, А2 - матрицы с элементами в виде констант.
Для обеспечения параллельности ГЦОИ БЛА и оси приведения необходимо, чтобы тензор инерции БЛА, записанный относительно координатных осей СК Ос^сУс^с» имел диагональный вид:
1бла -
^ххБЛА О
^у^БЛА О
^БЛАУ
То есть необходимо найти такое А1, при котором (16) будет иметь форму (17). Задачу можно поставить немного иначе: необходимо найти такое А1, при котором N + А1ТМ А1 будет иметь собственный вектор в виде орта Осхс базиса СК Осхсус^с- Задача в обеих постановках может быть решена итерационными методами. Существенно упрощает решение, ортогональность матрицы А1. После нахождения А1 вычисляется гскп из (1). В обеих постановках задача будет иметь несколько решений, поэтому можно ввести условия, обеспечивающие удовлетворение дополнительных требований к эксплуатационным характеристикам БЛА. Например, минимизация углов поворота полезного груза относительно корпуса, или минимизация абсолютной разницы значений поперечных главных центральных моментов инерции БЛА и^^бла “7^бла| .
Таким образом, показано, что для определения всех массогеометрических характеристик элементов баллистического летательного аппарата (корпуса и полезного груза), а именно значения масс элементов, трех координат центра масс, трех осевых и трех центробежных моментов инерции достаточно максимум трех циклов измерения массогеометрических характеристик БЛА. При этом на каждом цикле измерений производится внесение изменений в пространственное положение элементов. Сформулирована задача определения взаимной пространственной ориентации элементов баллистического летательного аппарата, удовлетворяющей требованиям конструкторской документации к массогеометрическим характеристикам баллистического летательного аппарата. Предложен подход к ее решению.
Список литературы Определение массогеометрических характеристик элементов баллистических летательных аппаратов
- Тверской, М.М. Автоматизированные стенды для контроля и расчёта коррекции распределения масс летательных аппаратов/М.М. Тверской//Динамика, прочность и износостойкость машин. -1995. -Вып. 1. -С. 69-77.
- Тверской, М.М. Автоматизированный контроль и коррекция распределения масс изделий машиностроения/М.М. Тверской. -Челябинск: Изд-во ЧГТУ, 1997. -184 с.
- Тверской, М.М. Контроль распределения массы летательного аппарата/М.М. Тверской//Вестник ЮУрГУ. Серия «Машиностроение». -2001. -Вып. 1. -С. 121-133.
- Фёдоров, В.Б. Контроль и коррекция массогеометрических характеристик летательных аппаратов: текст лекций/В.Б. Фёдоров. -Челябинск: Изд-во ЮУрГУ, 2004. -Ч. 1. -116 с.


