Определение механических характеристик износостойких ионно-плазменных покрытий на основе нитрида титана

или бицилиндрического наконечника – не нашло такого широкого применения при измерении твердости. В то же время измерение отпечатков малых размеров требует применения оборудования с высоким разрешением оптики.

В работе [2] для определения истинной твердости покрытий предлагается использовать метод экстраполяции на нулевую глубину проникновения индентора. При этом зависимость твердости системы “покрытие – инструментальная основа” от глубины проникновения индентора описывается выражением:

Н       ₊ H“ — H о

H С H О ⁺      ,2

1 + ^и- ,

a h

где HС – твердость системы “покрытие – инстру- ментальная основа”, Па;

ментальной основы, Па;

HО – твердость инстру-Нц - твердость покры- тия, Па; hи – глубина проникновения индентора,

м; h - толщина покрытия, м; a - коэффициент, м.

Таким образом, измерив твердость системы “по- крытие-инструментальная основа” при нескольких нагрузках, зная геометрические размеры индентора и твердость основы HО , можно найти коэффициент a и истинную твердость покрытия Нц .

Измерение микротвердости системы “покрытие – инструментальная основа” H_С покрытий по восстановленному отпечатку проводили на приборе ПМТ-3 с использованием пирамиды Виккерса. Обработку экспериментальных данных проводили с помощью математических пакетов Mathcad 2000 Professional и Microsoft Excel 2007.

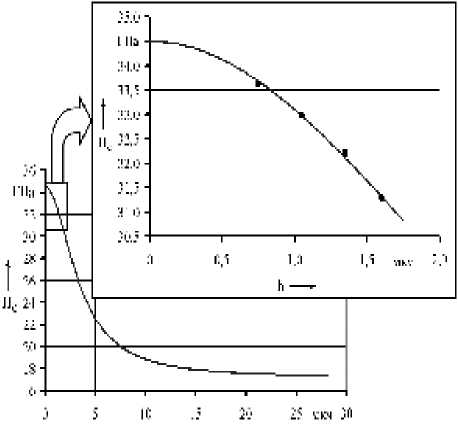
На рис. 1 в качестве примера показано влияние глубины проникновения индентора в покрытие TiCrN на величину микротвердости системы “покрытие – инструментальная основа”.

Таблица 1. Химический состав ионно-плазменных покрытий

Покрытие	TiAlN	TiZrN	TiSiN	TiFeN	TiCrN	TiMoN
Содержание легирующего элемента, % мас.	17,55	15,63	1,25	0,85	21,70	13,99

Таблица 2. Механические свойства ионно-плазменных покрытий

Покрытие	Микротвердость системы «покрытие – инструментальная основа» HC , ГПа, при нагрузке, Н				Микро-твердость 0 покрытия H µ , ГПа	Твердость покрытия по Мейеру HM, ГПа
	0,49	0,98	1,47	2,06
TiN	28,42	27,84	27,04	26,50	29,16	31,45
TiAlN	37,59	36,67	36,01	35,08	38,39	41,40
TiZrN	37,98	37,37	36,44	35,62	38,85	41,91
TiSiN	33,93	33,09	32,31	31,66	34,67	37,39
TiFeN	32,31	31,61	30,95	29,26	33,18	35,79
TiCrN	33,62	32,99	32,21	31,29	34,50	37,21
TiMoN	34,09	33,49	32,43	31,91	34,90	37,64

Примечание: микротвердость инструментальной основы (твердого сплава ВК6) – 17,05 ГПа

Другой важной механической характеристикой материала является модуль упругости первого рода Е (модуль Юнга). Традиционные методики определения его величины (испытания на растяжение – сжатие, изгиб, кручение) в случае изучения тонких покрытий применить невозможно. В работе [3] для определения модуля упругости первого рода предложена методика, основанная на индентировании поверхности испытуемого материала пирамидой Кнуппа. В результате упругого восстановления размеры отпечатка после снятия нагрузки искажаются по сравнению с размерами самого индентора. Зависимость между модулем упругости первого рода и размерами пирамиды Кнуппа и отпечатка микротвердости имеет вид:

1__*.

Рис. 1. Зависимость микротвердости системы “покрытие TiCrN – инструментальная основа ВК6” от глубины проникновения индентора: • – экспериментальные данные;

^^^^^^м – теоретическая зависимость

b' d'

b d

-

H α ^K

E,

где b и d – длины меньшей и большей диагона-

лей пирамиды Кнуппа (рис. 2, б) ( d = 7 11 ); b’

Используя величину микротвердости H⁰_µ , полученную из выражения (1), можно определить твердость покрытия по Мейеру НМ по формуле:

HM

Hµ0

sin 68

Результаты измерений и расчетов микротвердости H_C и H ⁰ _µ и твердости по Мейеру HM ионно-плазменных покрытий представлены в табл. 2.

и d’ – длины меньшей и большей диагоналей отпечатка (рис. 2, б); α – коэффициент ( α = 0,45 ); H_K – микротвердость по Кнуппу.

На рис. 2 показаны отпечаток пирамиды Кнуппа на поверхности покрытия TiN и расчетная схема для определения модуля упругости первого рода.

Модуль упругости первого рода можно определить используя метод кинетической микротвердости [4, 5], заключающийся в построении диаграммы вдавливания (рис. 3).

Величина модуля упругости определяется по кривой разгружения по формуле [5]:

E =

1 -v ²

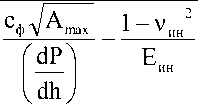
где v — коэффициент Пуассона материала покрытия; Еин , vин — модуль упругости первого рода и коэффициент Пуассона материала индентора (E = 950ГПа ; v = 0,07); с — постоян-ин                  ин             ф ная (для пирамиды Виккерса сф=1,142), dP ^ dh J

производная нагрузки по глубине проникновения индентора в начале кривой разгружения, Н/м; Аmax – максимальная площадь отпечатка, м2.

Максимальная площадь отпечатка Аmax определяется по формулам [5]:

A max = (9,96 - 12,64(1 - S) + 105,42(1 - S)² -

- 229,57(1 - S) 3 + 157,67(1 - S)⁴)^,

^S =г [ 1 - rr-)                     ⁽⁵⁾

d < max У где kd – коэффициент формы индентора (для пирамиды Виккерса kd = 5).

Результаты исследований механических характеристик при испытании износостойких покрытий методом кинетической микротвердости и индентированием пирамидой Кнуппа представлены в табл. 3.

Из полученных результатов видно, что оба метода измерения модуля упругости первого рода дают близкие результаты. Расхождение между полученными результатами измерений не превышает 7%.

Одной из основных механических характе-

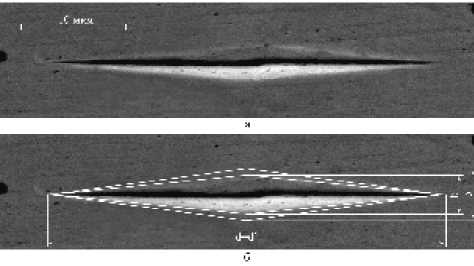
Рис. 2. Фотография отпечатка (а), полученного на покрытии TiN при индентировании пирамидой Кнуппа при нагрузке 2,55 Н и расчетная схема для определения величины модуля упругости первого рода Е (б).

Инструментальная основа – твердый сплав ВК6

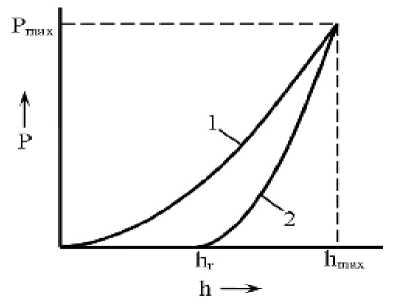
Рис. 3. Диаграмма вдавливания [5]:

1 – кривая нагружения; 2 – кривая разгружения; Pmax – максимальная нагрузка; hmax – максимальная глубина проникновения индентора; hr – остаточная глубина проникновения индентора при снятии нагрузки

ристик материала покрытия является предел текучести. Для объемных материалов его определение основано на построении диаграмм растяжения или сжатия. Для тонких хрупких покрытий, которые к тому же никак нельзя отделить от инструментальной основы, этот метод применить невозможно. В этом случае предел текучести материала покрытия можно определить косвенными методами, основанными на связи предела текучести с твердостью и модулем упругости первого рода [4, 5].

В работе [4] для определения величины предела текучести с т твердых малопластичных материалов предложена зависимость, полученная Р. Хиллом в виде:

q 2 1     3 ,         3

— = — 1 +--ln---------- с т 3 L 3 - A A + 3B - AB

A = (1 - 2 v ) S

B = (1 +v ) С т

где q - среднее контактное давление, Па; v -коэффициент Пуассона.

Для покрытия TiN коэффициент Пуассона, согласно работе [6], равен 0,29. Учитывая, что легирование материалов не приводит к существенному изменению его величины [7], это значение можно использовать и для покрытий сложного состава.

Величину контактного давления q в формуле (6) согласно рекомендациям работы [4] приближенно можно взять равной твердости по Мейеру HM. Однако для твердых материалов различие между этими значениями может достигать значительной величины, что может при-

Таблица 3. Результаты исследований механических характеристик при испытании износостойких покрытий методом кинетической микротвердости* и индентированием пирамидой Кнуппа**

П окрытие	max , Н	h max , мкм	h r , мкм	f dP ) 1 dh J , МН/м	Е*, ГПа	Е**, ГПа
TiN	0,5	1,30	0,65	1,538	307	311
TiAlN		1,26	0,63	1,587	369	347
T iZrN		1,25	0,62	1,587	379	393
TiSiN		1,28	0,64	1,563	350	337
TiFeN		1,29	0,65	1,563	332	312
TiCrN		1,28	0,63	1,538	344	-
TiMoN		1,28	0,65	1,587	358	-

вести к большой погрешности при расчете предела текучести. Учитывая вышесказанное и используя данные работы [8] по измерению твердости, в Mathcad 2000 Professional была получена регрессионная зависимость между твердостью по Мейеру HM и средним контактным давлением q:

q = 1 - 0,23 f HM ) + 4,35б Г HM

HM I E J I E

^^^^^^^^

-

27,233 1

HM

1,5

-

24,539 1

E

HM

2,5

E

+ 45,586 1

HM

-

.

E

. (7)

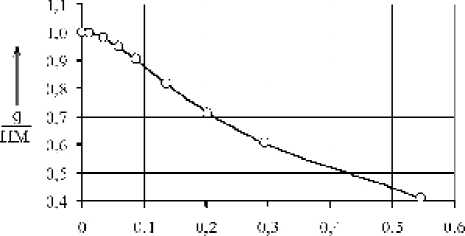
Экспериментальная проверка полученной зависимости (7) показала хорошее соответствие между расчетными и экспериментальными данными (рис. 4).

На основе полученной зависимости (7) и экспериментальных значений твердости HM (табл. 2) были рассчитаны значения контактного давления q и предела текучести с _т для различных износостойких покрытий (табл. 4).

Из представленных данных видно, что леги-

рование покрытий приводит к увеличению значения предела текучести на 17…30%. Это связано с повышением сопротивления упруго-пластической деформации сложных растворов замещения на основе нитрида титана, что косвенно подтверждается также увеличением твердости и модуля упругости первого рода покрытий.

В механике разрушения для оценки сопротивления хрупких материалов процессам развития трещины используют понятие критического коэффициента интенсивности напряжений K_IC . Выражение для его определения получено на основании математического анализа распространения в непрерывной упругой среде бесконечно острой трещины при абсолютно хрупком разрушении материала, т. е. при условии, что у вершины трещины отсутствует проявление его пластических свойств. В то же время в работах [9 – 11] отмечается, что хрупкому разрушению реальных материалов всегда предшествует определенная пластическая деформация, возникающая около ее вершины. Величина зоны пластических деформаций и ее интенсивность зависят прежде всего от механических свойств материала. Для учета запаса пластичности материала при развитии трещины используют понятие вязкости разрушения K_ICП . При этом для расчета величин K_IC и K_ICП применяют одно и то же уравнение [9, 12].

Критический коэффициент интенсивности напряжений K_IC , согласно работе [9], определяется по формуле:

_ _ I 2E y

K IC лк 2 , (8)

V 1 — V

где Y - поверхностная энергия твердого тела, Дж/м².

Вязкость разрушения K_ICП можно определить как [12]:

им к

Рис. 4. График зависимости

q = f f HM

К ICП

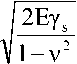
HM

E

– расчетная кривая;

– экспериментальные данные

где Y s — эффективная поверхностная энергии, Дж/м², равная сумме поверхностной энергии твердого тела Y и удельной работы пластичес-

Таблица 4. Механические свойства износостойких покрытий

Покрытие	q, ГПа	σ т , ГПа	а, нм	с, мм	С с	Критический коэффициент интенсивности напряжений K IC , МПа • м1/2	Вязкость разрушения K ICП , МПа • м1/2
TiN	26,25	9,53	0,4235	0,126	2,49	3,39	12,29
TiAlN	33,20	12,26	0,4230		2,62	4,07	14,77
TiZrN	33,66	12,38	0,4293		2,75	4,22	14,44
TiSiN	30,55	11,17	0,4256		2,45	3,88	14,46
TiFeN	31,01	11,61	0,4234		2,92	3,67	12,59
TiCrN	32,22	11,80	0,4224		2,88	3,80	13,04
TiMoN	32,79	11,26	0,4251		2,63	3,96	13,84

кой деформации материала у конца трещины у пл .

При исследовании прочностных свойств относительно хрупких материалов более часто используют величину критического коэффициента интенсивности напряжений K_IC . Использование такой характеристики объясняется простотой ее расчета. Кроме того, считается, что вклад работы у пл , затрачиваемой на пластическую деформацию материала у конца трещины, невелик и можно считать, что у _s «у (или, соответственно, K_ICn « K IC ). Такой подход был использован в работе [13] при оценке трещиностойкости износостойких покрытий. В то же время экспериментальные данные показывают [9, 14], что величина K_IC дает заниженное значение прочности даже для относительно хрупких материалов, где пластические деформации невелики.

Для определения критического коэффициента интенсивности напряжений K_IC в работе [14] предложена энергосиловая модель разрушения межатомных связей в кристалле, исходя из силового критерия С. Инглиса. Согласно работе [14], величина K_IC равна:

Как видно из зависимости (12), для расчета критического коэффициента интенсивности напряжений необходимо знать размеры периода кристаллической решетки материала покрытий. Измерение величины а проводили на дифрактометре “ДРОН-3М” с использованием фильтрованного Cuкб-излучения. Полученные результаты представлены в табл. 4.

При разрушении покрытий, трещины возникающие в них, распространяются в направлении, перпендикулярном границе раздела “покрытие – инструментальная основа”. Для таких трещин (трещины Палмквиста [4]) величину вязкости разрушения K_ICП можно определить по формуле [4]:

K ICП

т

Г

E

0.4

C

-

V°т 7

c

K IC

^О теор       ^{а п}

"2Kp(i -V ²)

где a – период кристаллической решетки, м; о _теор - теоретическая прочность кристалла, Па, K – коэффициент, учитывающий нелинейность эффектов для предельно напряженного состояния в конце трещины и среду ее распространения и приблизительно равный 0,107.

Величину о _теор можно определить как [15]:

E

° ^теор = 4 п (1 -V ²) .            ⁽¹¹⁾

Подставляя выражение (11) в (10), получим:

K IC

Ea

8K(1 -V ²)р л (1 -V 2 ) .

где с – размер отпечатка, м; С – длина трещины Палмквиста, м.

Схема образования трещин Палмквиста при индентировании покрытий пирамидой Виккерса показана на рис. 5, а на рис. 6 представлена фотография такого отпечатка, полученного на покрытии TiAlN.

Результаты расчета критического коэффициента интенсивности напряжений K_IC и вязкости разрушения K_ICП для различных покрытий представлены в табл. 4. Как видно из данных табл. 4, величина вязкости разрушения K_ICП больше критического коэффициента интенсивности напряжений K_IC в 3,4…3,7 раза. Это свидетельствует об упруго-пластическом разрушении материала покрытия при развитии в нем трещин. Поэтому для расчета сопротивления процессам развития трещины материалов износостойких ионно-плазменных покрытий на основе нитрида титана необходимо использовать величину вязкости разрушения K_ICП , а не критического коэффициента интенсивности напряжений K_IC . Последний может лишь служить для грубой предварительной

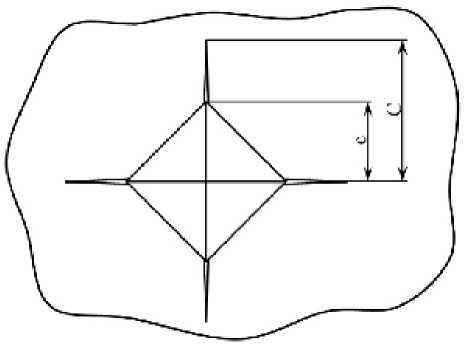
Рис. 5. Схема образования трещин Палмквиста при индентировании пирамидой Виккерса [4]

оценки на начальном этапе выбора материала износостойкого покрытия.

Следует также отметить, что для покрытий сложного состава наблюдается увеличение как значения критического коэффициента интенсивности напряжений K_IC (на 8…25%), так и величины вязкости разрушения K_ICП (на 2…20%). Это в первую очередь связано с изменением таких механических характеристик материалов покрытий, как твердость по Мейеру HM, модуля упругости первого рода Е и предела текучести σ _Т .