Определение механических свойств артерий виллизиевого многоугольника

Функционирование нейронов мозга требует значительных затрат энергии, которую мозг получает через сеть кровоснабжения. Всего кровоснабжение головного мозга обеспечивают четыре артерии – две сонные и две позвоночные, по их руслу к мозгу транспортируется до 20% всего объема крови. Уже в полости черепа сонная артерия имеет продолжение в виде передней и средней мозговых артерий (ПМА и СМА), позвоночные артерии (ПА) сливаются на уровне ствола головного мозга в основную артерию (базилярную артерию), которая далее продолжается уже в качестве двух задних мозговых артерий (ЗМА). Перечисленные три пары артерий (передняя, средняя, задняя) анастомозируя между собой, образуют виллизиев многоугольник (рис. 1).

Для этого передние мозговые артерии соединяются между собой передней соединительной артерией (ПСА), а между средней и задней мозговой артерией с каждой стороны имеется задняя соединительная артерия (ЗСА). Подобное «нормальное» строение встречается в 25% случаев.

Одним из самых опасных и часто встречающихся заболеваний сосудов виллизиевого многоугольника являются аневризмы (местное расширение артерий) [2]. Наиболее частой локализацией аневризм являются бифуркации сосудов: места отхождения передней и средней мозговой артерий от внутренней сонной, места соединения передней соединительной и передней мозговой артерий, внутренней сонной и задней соединительной артерий. Иногда встречаются множественные аневризмы сосудов основания мозга. При разрыве аневризмы кровь может проникать в вещество мозга и прорываться в желудочки: появляется клинический синдром субарахноидально-паренхиматозной или субарахноидально-паренхиматозно-вентрикулярной геморрагии.

Передняя мозговая артерия

Средняя мозговая артерия

Внутренняя сонная артерия

Задняя мозговая артерия

Базилярная артерия

Позвоночная артерия

Рис. 1. Схема замкнутого виллизиевого многоугольника

Современные исследования позволили обнаружить доказательства того, что существуют врожденные, приобретенные и наследственные дефекты артериальной стенки [4]. Большинство аневризм развивается из-за гемодинамических и дегенеративных повреждений стенки, а не, как считалось ранее, из-за наследственных факторов. Считается [4], что распространенность, рост, наличие тромбов в полостях и даже разрыв аневризм могут быть объяснены с помощью гемодинамики. В связи с этим возникает необходимость в выявлении механических факторов появления и развития аневризм, исследовании процессов, происходящих в местах их локализации. Для этого необходимо математическое моделирование поведения сосудов виллизиевого круга, которое, в свою очередь, требует знания механических свойств стенок артерий.

Испытания на растяжение образцов артерий

В экспериментах использовалась разрывная машина Tiratest 28005 (зарегистрированная под номером 23512–02 в Государственном Реестре Российской Федерации) с нагрузочной ячейкой 100 Н. Данная машина позволяет испытывать образцы на растяжение и сжатие в одном направлении.

Сосуды для исследования на одноосное растяжение в продольном направлении были взяты у 97 мужчин и женщин в возрасте от 21 до 87 лет и у 12 трупов людей для исследования на одноосное растяжение в поперечном направлении не позднее 12 часов после смерти. До начала экспериментов образцы сохранялись в физиологическом растворе при температуре (20±1)°С, что, как известно, не влияет на их механические свойства [3]. Эксперименты проводили также при температуре (20±1)°С.

Все образцы были поделены на две группы по половому признаку и на четыре возрастные группы (см. табл. 1: возраст на момент смерти 22–90 лет соответствует возрастным группам с первой по четвертую как для мужчин, так и для женщин).

Обработка результатов экспериментов показала возрастные изменения, а также половые различия материала стенок артерий.

Диаграмма ( σ-λ ) ( σ – напряжение, λ – степень удлинения) имеет нелинейный характер (рис. 2) при растяжении как в продольном направлении, так и в поперечном.

Средние по возрастным группам пределы прочности в продольном направлении исследуемых артерий представлены в табл. 2–4.

Таблица 1

Возрастные и половые группы

Номер возрастной группы	Возраст, лет
	мужчины	женщины
1	22–35	21–35
2	36–60	36–55
3	61–74	56–74
4	75–90	75–90

Таблица 2

Средние по возрастным группам пределы прочности (МПа) в продольном направлении ______________ для базилярной артерии, правой ПМА, левой ПМА ____________________

	Базилярная		Правая ПМА		Левая ПМА
Возр. гр.	мужчины	женщины	мужчины	женщины	мужчины	женщины
1	1,76	1,60	1,48	1,14	1,51	1,36
2	1,35	1,22	1,26	1,10	1,40	1,25
3	0,97	0,89	1,01	0,93	1,18	1,02
4	0,90	0,81	0,97	0,79	1,04	0,94

Таблица 3

Средние по возрастным группам пределы прочности (МПа) в продольном направлении для правой СМА, левой СМА, правой ЗМА, левой ЗМА

	Правая СМА		Левая СМА		Правая ЗМА		Левая ЗМА
Возр. гр.	мужчины	женщины	мужчины	женщины	мужчины	женщины	мужчины	женщины
1	1,16	1,29	1,09	1,38	1,44	1,25	1,16	1,29
2	1,04	1,11	0,99	1,15	1,21	1,16	1,04	1,11
3	0,82	0,59	0,61	0,54	1,02	0,97	0,82	0,59
4	0,70	0,63	0,77	0,76	0,97	0,93	0,70	0,63

Таблица 4

Средние по возрастным группам пределы прочности (МПа) в продольном направлении для правой ЗСА, левой ЗСА, правой ПА, левой ПА

	Правая ЗСА		Левая ЗСА		Правая ПА		Левая ПА
Возр. гр.	мужчины	женщины	мужчины	женщины	мужчины	женщины	мужчины	женщины
1	1,45	0,00	1,48	1,41	2,21	1,93	1,45	0,00
2	1,00	0,94	1,26	1,37	2,04	1,79	1,00	0,94
3	0,98	0,88	1,10	1,11	1,66	1,69	0,98	0,88
4	0,93	0,82	0,95	0,94	1,36	1,23	0,93	0,82

Таблица 5

Средние по возрастным группам максимальные относительные удлинения в продольном направлении базилярной артерии, правой ПМА, левой ПМА

	Базилярная		Правая ПМА		Левая ПМА
Возр. гр.	мужчины	женщины	мужчины	женщины	мужчины	женщины
1	0,35	0,36	0,29	0,39	0,40	0,43
2	0,40	0,39	0,26	0,23	0,27	0,28
3		0,43	0,23	0,26	0,27	0,28
4	0,33	0,38	0,25	0,32	0,43	0,26

Таблица 6

Средние по возрастным группам максимальные относительные удлинения в продольном направлении для правой СМА, левой СМА, правой ЗМА, левой ЗМА

	Правая СМА		Левая СМА		Правая ЗМА		Левая ЗМА
Возр. гр.	мужчины	женщины	мужчины	женщины	мужчины	женщины	мужчины	женщины
1	0,52	0,56	0,45	0,39	0,44	0,42	0,52	0,56
2	0,44	0,58	0,43	0,45	0,45	0,42	0,44	0,58
3	0,33	0,44	0,33	0,37	0,24	0,41	0,33	0,44
4	0,40	0,25	0,42	0,39	0,36	0,29	0,40	0,25

Таблица 7

Средние по возрастным группам максимальные относительные удлинения в продольном направлении для правой ЗСА, левой ЗСА, правой и левой нижних передних мозжечковых артерий (НПМА)

	Правая ЗСА		Левая ЗСА		Правая НПМА		Левая НПМА
Возр. гр.	мужчины	женщины	мужчины	женщины	мужчины	женщины	мужчины	женщины
1	0,44	0,47	0,60	0,33	0,25		0,44	0,47
2	0,42		0,35		0,33		0,42
3		0,36		0,37	0,07	0,45		0,36
4	0,20	0,33	0,35	0,46	0,25		0,20	0,33

Таблица 8

Средние по возрастным группам максимальные относительные удлинения в продольном направлении для правой и левой задних нижних мозжечковых артерий (ЗНМА), правой и левой ВМА

	Правая ЗНМА		Левая ЗНМА		Правая ВМА		Левая ВМА
Возр. гр.	мужчины	женщины	мужчины	женщины	мужчины	женщины	мужчины	женщины
1	0,57	0,25			0,36	0,53	0,57	0,25
2	0,20	0,32	0,30	0,34	0,37	0,22	0,20	0,32
3	0,07	0,26		0,18		0,30	0,07	0,26
4				0,22	0,38	0,21

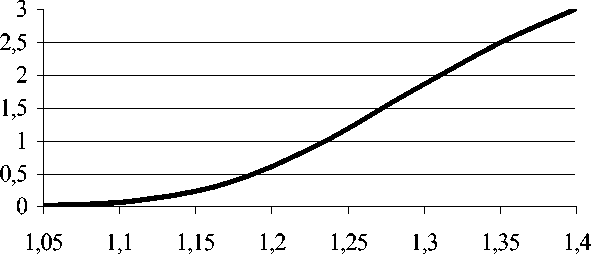
λ, м

Рис. 2. Диаграмма «напряжение ( σ ) – степень удлинения ( λ )» ( σ-λ )

Возрастные группы

ф Базилярная

• ■ Пр авая ПМА

* Левая ПМА

Пр авая СМА

Левая СМА

• • Пр авая ЗМА

Левая ЗМА

'     Пр авая ЗСА

• —^^^— Левая ЗСА

ф Пр авая ПА

• ■ Левая ПА

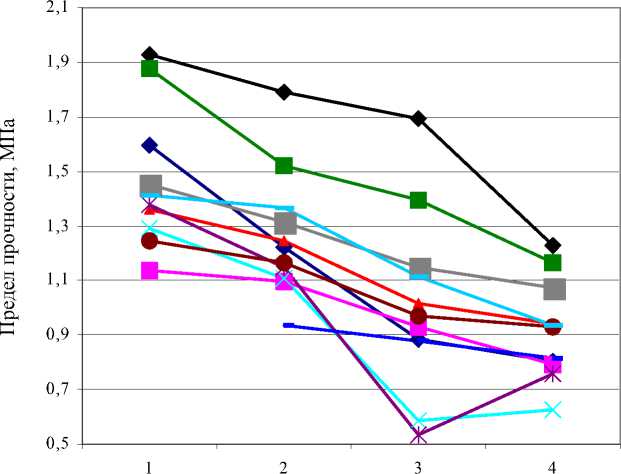
Рис. 3. Средние по возрастным группам пределы прочности в продольном направлении (мужчины)

Пределы прочности во всех исследованных артериях, взятых у женщин, меньше, чем у мужчин. С возрастом предел прочности артерий в продольном направлении уменьшается. При этом наибольшая разница между пределами прочности для первой и четвертой возрастных групп выявлена у базилярной артерии, она составляет порядка 50%. Для остальных артерий эта разница не более 30–40%. Наибольшие половые различия предела прочности в продольном направлении были выявлены у позвоночных артерий, этот же предел прочности у позвоночных артерий является максимальным как у женщин, так и у мужчин.

Графики возрастных изменений среднего по возрастным группам предела прочности артерий виллизиевого многоугольника показаны на рис. 3 (мужчины), на рис. 4 (женщины).

Практически для всех артерий характерно снижение деформативности с возрастом. Но для некоторых артерий у женщин и мужчин четвертой возрастной группы деформативность возрастает по сравнению с третьей группой. В продольном

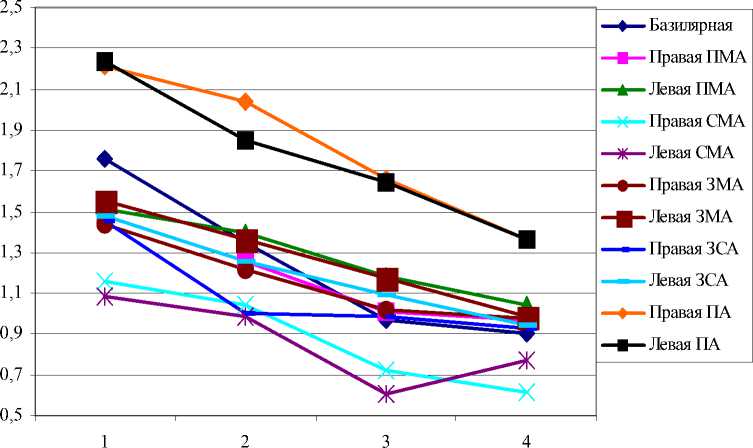
Возрастные группы

Рис. 4. Средние по возрастным группам пределы прочности в продольном направлении (женщины)

направлении стенки средней мозговой артерии обладают наибольшей деформативностью по сравнению с другими артериями виллизиевого многоугольника.

Предел прочности в поперечном направлении так же, как и в продольном направлении, снижается с возрастом. При этом наибольшие по величине возрастные изменения предела прочности характерны для базилярной артерии.

Получение параметров модели

Проведем расчет параметров модели сверхупругого резиноподобного материала Муни–Ривлина [1, 6]. Для этого выведем зависимость напряжение–степень удлинения для одноосного растяжения с использованием функции энергии деформации данного материала.

Рассмотрим правый и левый тензоры деформации Коши–Грина C = F T F , B = FF^T соответственно, где F - тензор градиента деформации. Инварианты правого тензора С (аналогично для левого) определяются соотношениями 1 1 = tr ( C ) , 1 2 = 2 ( 1 12 - tr ( C ² ) ) , 1 3 = det ( C ) . Материал стенки артерии принято считать несжимаемым [5], поэтому 1 3 = 1. Тензор градиента деформации в матричной форме можно записать в виде

F =

1%

0   0 )

X ₂ 0

0 X 3 J

где   X1, X2, X3 - степени удлинения. В этом случае правый и левый тензоры деформации Коши–Грина совпадают:

C = B = F x

■

x 2

X 2 ,

.

Инварианты для тензора С определяются следующими выражениями:

1 1 = x f + x 2 +X 2 ,

1 2 = 2 ( 1 22 - tr ( c ² ) ) =

111 x f ⁺ x f ⁺ x f ’

1 ₃ = det ( C ) = det ( F ² ) = ( X 1 X ₂ X ₃ )2 = 1.

Выражения для напряжений, возникающих в растягиваемом образце, через функцию энергии деформации W записываются следующим образом:

• о.. = Х 2 Ф—-T + p ,

ii i        x 2

dW W где Ф = 2---, T = 2--- [1]. Для несжимаемого материала функция энергии

d11          d12

деформации зависит только от первых двух инвариантов W = W ( 1 1 , 1 ₂ ) .

В случае одноосного растяжения он * 0, о22 о;; = 0. Рассмотрим равенство о33 = 0. Отсюда X3Ф  T + p = 0, p = —T~X3Ф. Подставим полученное выражение Х3                 хз дляр в Си, Сзз • о! = X,!Ф ■ T + T _ Х2Ф = (Х2 ■ X32) Ф

11      1       Х2        Х32          3 V 1      3V

о„ =x 2 Ф" -¹- t+ Л t~x 2 ф = (х 2 "X 2 )ф 22  2   223    2  3

X 2     Хз

С учетом несжимаемости (Х3 = —— ) получим

Х1Х 2

^O 22

x 2

On = X f

XX 2

ф_

X 2

x2x 2

X ³

t,

|т

3 2 ^T ’

T.

XX2

Ф

X2

xfx 2

t= x 2

XX2

Учитывая, что с ₂₂ = 0, имеем X 2 ~

/ 9 = 0 «

Х 2 Х 2

X 4 = Л « «X 2 = -¹. Тогда ^X i                    ^X i

(обозначив X 1 = X )

O11

X ²

X1

Ф

x 2

X2- Т= X2 — Ф

X J I X)

x 2

X |T = | X ²

¹ II Ф + ¹ T I . xJI X )

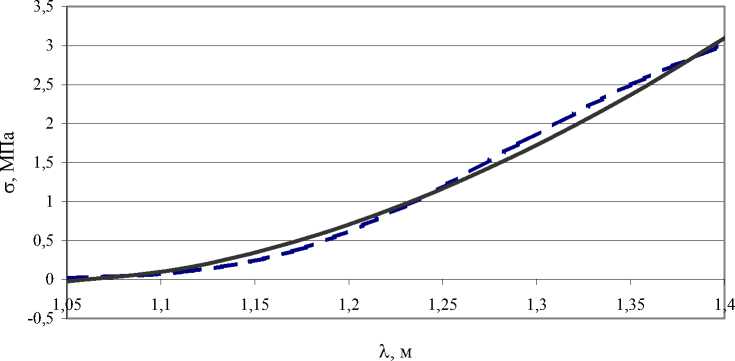
Рис. 5. Диаграммы a-X . Сплошная линия получена по формуле (1), пунктирная -

экспериментальная кривая

2 2            1

Инварианты тензора примут вид I_x = X + , I^ = — + 2 X . Окончательно X ² X ²

получаем зависимость напряжения от степени удлинения в случае одноосного растяжения в виде a = 2

X ²

1 Vd W 1 5 W )

I +

X Д 511  X 512 / где X = -— отношение длины образца к начальной длине образца.

l0

Рассмотрим функцию энергии деформации Муни–Ривлина [1]

W = с ,( I , - 3 ) + C 2 ( 1 2 - 3 ) .

Тогда а = 2 X2 - C + 2 X- C.

V X/ V X у

Таким образом, имея данную зависимость и результаты эксперимента на одноосное растяжение, можно получить коэффициенты функции энергии деформации с помощью метода наименьших квадратов.

Расчет констант C ₁ , C ₂ , имеющих размерность напряжений, проводился в системе компьютерной алгебры Matlab ( MathWorks Inc .). Данные диаграммы ( a-X ) одноосного растяжения образца базилярной артерии виллизиевого многоугольника импортировались в Matlab ( MathWorks Inc. ), далее по экспериментальной кривой интерполяционным методом были выбраны точки для определения констант методом наименьших квадратов.

На рис. 5 представлены следующие кривые: пунктирная линия – зависимость ( a-X ), построенная по интерполированным точкам экспериментальных данных, сплошная линия - зависимость ( a-X ), полученная по формуле (1) с найденными константами C ₁ = 5,2 Па, C ₂ = –5,54 Па.

Как видно из рис. 5, теоретическая кривая (сплошная линия) достаточно хорошо приближает экспериментальную (пунктирная линия). И все же выбранная функция энергии деформации Муни–Ривлина в будущем будет заменена на другую, более сложную, которая позволит учесть точку перегиба на экспериментальной диаграмме ( σ-λ ).