Определение механических свойств материалов на основе моделей взаимодействия зонда атомно-силового микроскопа с поверхностью образцов

Атомно-силовой микроскоп (АСМ) относится к классу сканирующих зондовых микроскопов. Принцип его работы основан на регистрации взаимодействия зонда с поверхностью изучаемого объекта. При сканировании зонд, расположенный на свободном конце кантилевера — упругой консольной балки с одним жестко закрепленным концом, движется по исследуемой поверхности, повторяет неровности ее рельефа и влечет за собой изгиб кантилевера. Отклонения кантилевера от первоначального положения регистрируются и передаются в блок управления и компьютер; происходит обработка сигнала и дается команда о перемещении зонда в следующую точку поверхности. Таким образом, точка за точкой строится пространственное изображение поверхности образца.

Изобретение АСМ связано с развитием сканирующей туннельной микроскопии (СТМ). В 1981 г. сотрудники компании IBM Герд К. Биннинг и Генрих Рорер впервые представили прототип современного

сканирующего туннельного микроскопа (СТМ). За изобретение СТМ в 1986 году Биннингу и Рореру была присуждена Нобелевская премия по физике. В том же году Бинниг совместно с К. Куэйтом и К. Гербером представил прототип атомно-силового микроскопа [1], а через два года началось их серийное коммерческое производство.

К преимуществам АСМ относится то, что он позволяет:

– исследовать практически любые твердые и мягкие материалы, при этом, в отличие от сканирующей электронной микроскопии, поверхность диэлектриков не требует нанесения проводящего покрытия;

– изучать локальные механические, электрические, магнитные и другие характеристики;

– проводить измерения не только в комнатных условиях, но и в вакууме, жидкости, при пониженной или повышенной температуре. К слову, в 2008 году Американское космическое агентство (NASA) отправило на Марс зонд, на борту которого в числе прочего оборудования находился АСМ для изучения микроструктуры марсианской пыли в полевых условиях [2].

Недостатками АСМ являются:

– относительно низкая скорость получения изображения (порядка минут); изменения поверхности образца во времени (температурный дрейф, релаксация, подвижность живой клетки) могут привести к искажению изображения (следует отметить, что новейшие АСМ лишены этого недостатка и формируют изображения практически в реальном времени);

– влияние, оказываемое структурно-механическими свойствами зонда на результаты измерений;

– небольшие по сравнению с электронной сканирующей или оптической микроскопией размеры исследуемой области (размер изображения в плоскости обычно не превышает 100 х 100 мкм, а предельный перепад высот дефектов поверхности изучаемой области 10 мкм).

В работе АСМ можно выделить два основных режима механического взаимодействия зонда с образцом: статический и динамический. В статическом режиме кантилевер с зондом приближаются к образцу, зонд контактирует с поверхностью и затем кантилевер отводится. Вся информация о взаимодействиях зонда с образцом содержится в изменении параметра d — отклонения от горизонтального положения свободного конца кантилевера при движении вверх-вниз в направлении z закрепленного основания кантилевера (Рис. 1).

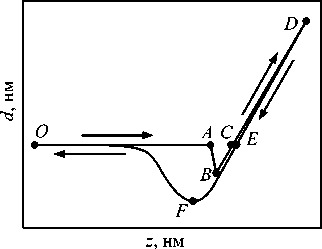
Рис. 1. Силовая кривая – отклонение зонда в зависимости от вертикального перемещения основания кантилевера ( а ), и соответствующие схемы движения вверх-вниз пары «кантилевер–зонд» ( б )

б

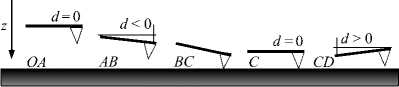
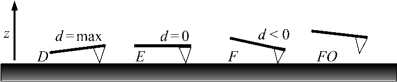
Приближение зонда к поверхности — прямой ход ( OABCD ), состоит из нескольких этапов. На 1-м этапе — на отрезке OA — зонд находится вдали от поверхности материала, при этом d ® 0 . На 2-м этапе — на отрезке AB — зонд, оставаясь на некотором расстоянии над поверхностью, начинает притягиваться к ней. Притяжение может быть вызвано совокупностью факторов: действием сил Ван-дер-Ваальса, электромагнитными и капиллярными взаимодействиями зонда с образцом (так, в комнатных условиях любая поверхность всегда покрыта адсорбированным слоем воды толщиной 2–4 нм [3–5]). В точке B — на 3-м этапе — происходит касание зонда поверхности. Если материал достаточно мягкий, а кантилевер жесткий, то положение B отвечает началу вдавливания (индентации) зонда в образец. На 4-м этапе — на отрезке BC — зонд упирается в образец, а закрепленный конец кантилевера продолжает движение вниз. То есть отклонение кантилевера от горизонтали уменьшается. Участок CD — 5-й этап — соответствует дальнейшему нажиму зонда на образец, отклонение d увеличивается вплоть до максимального значения d _max в точке D . После этого основание кантилевера начинает двигаться в противоположном направлении и совершает обратный ход — DEFO , вызывая уменьшение d .

На обратном ходе заслуживает внимания отрезок EF — здесь зонд удерживается около поверхности материала за счет адгезионных взаимодействий. В точке F сила адгезии достигает своего максимального значения. Далее сила адгезии ослабевает, и зонд отрывается от поверхности образца. При совпадении участков CD (прямой ход) и DE (обратный ход) взаимодействие зонда с образцом является упругим. В противном случае на результатах будет сказываться также влияние вязких и/или пластических свойств материала.

Усилие нажима зонда на образец определяется как F = kd , где к — изгибная жесткость кантилевера. В общем случае каждый шаг перемещения основания кантилевера A z влечет за собой изменения отклонения кантилевера от предыдущего положения на величину A d и глубины внедрения зонда A5 в материал: A z = A d + A5 . Отсюда можно получить глубину индентации 5 .

В статическом режиме имеется возможность исследовать трение зонда о поверхность материала: зонд прижимается к поверхности и движется в направлении, ортогональном оси кантилевера. Эксперименты данного вида проводятся достаточно редко и в настоящей работе не рассматриваются.

В динамическом (полуконтактном, колебательном) режиме кантилевер осциллирует вблизи поверхности образца. Изменение амплитуды и фазы колебаний при кратковременном прерывистом контакте зонда с поверхностью отображает информацию о рельефе поверхности образца и механических свойствах его материала.

Существует также смешанный режим, так называемая силовая модуляция, когда силовые кривые строятся с частотой ~ 1 кГц, а их обработка осуществляется «статическими» методами анализа. Преимущество таких режимов — высокая скорость работы, а следовательно, возможность картирования механических свойств целых областей.

Для статического и динамического режимов существуют различные аналитические и численные модели движения кантилевера с учетом и без учета взаимодействия «зонд–поверхность образца» [6–8]. Кантилевер представляется при этом в виде сосредоточенной массы на пружине или как сплошная балка [9–12].

• 2.    Зонд в виде массы на пружине

  • 2.1.    Статические взаимодействия зонда с поверхностью

В механике контактного взаимодействия существует большое число моделей, описывающих упругую деформацию двух тел. Эти модели отличаются определением контактного радиуса, деформации и силы адгезии. В литературе, как правило, описываются три основные: модель Герца, модель Дерягина - Мюллера - Топорова (модель ДМТ) и модель Джонсона - Кендалла - Робертса (теория ДжКР) (Рис. 2). Причиной их популярности является простота применения, а также хорошее согласование теоретических данных и экспериментальных результатов. Другие существующие модели представляют собой модификацию трех перечисленных.

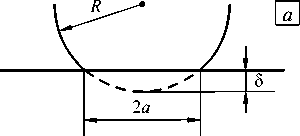
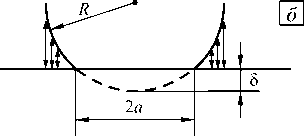
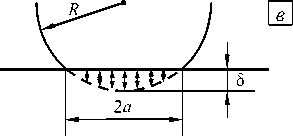
Рис. 2. Упругий контакт сферы и плоскости в моделях Герца ( а ), ДМТ ( б ), ДжКР ( в ) (двухсторонние стрелки означают зону действия сил адгезии)

Впервые достаточно точный анализ напряжений при контакте двух упругих тел проведен Герцем в 1882 году [13]. Он предположил, что в общем случае область контакта имеет эллиптическую форму, а для вычисления локальных деформаций каждое тело может рассматриваться как упругое полупространство, нагруженное по малой эллиптической части его поверхности. Следовательно, напряжения вблизи зоны контакта можно исследовать независимо от общих распределений напряжений в контактирующих телах, форма и способы закрепления которых обуславливают эти напряжения. При этом применимы те же методы решения краевых задач, что и для упругого полупространства.

Модель Герца используется, если характерные размеры области контакта малы по сравнению с размерами каждого из контактирующих тел и радиусами кривизны их поверхностей (выполнение условия необходимо для того, чтобы поверхности, располагающиеся вблизи области контакта, но находящиеся за ее пределами, можно было считать близкими к плоской поверхности полупространства, и чтобы деформации в области контакта были достаточно малыми и позволяли оставаться в рамках линейной теории упругости); поверхности контактирующих тел можно считать гладкими (следовательно, в контактной области могут действовать только нормальные давления, силы трения и адгезии во внимание не принимаются); не учитывается поверхностная энергия.

В случае контакта абсолютно жесткой сферы радиуса R (острия зонда АСМ) и деформируемой плоскости (исследуемого материала) (Рис. 2а) радиус a окружности контактной зоны и глубина индентации (деформация плоскости) 5 выражаются как a = (3 RF/(4 E * ))V3

и 5 = a ² / R .

Здесь: F — внешняя нагрузка; E* — приведенный модуль упругости, 1]E* = ( 1 -v p ) ^p + ( 1 -v ² ) ^Es , где v p , E p и v s , E s — коэффициенты Пуассона, модули упругости зонда (индекс p ) и исследуемого материала (индекс s ). После подстановки а в формулу для 5 и предположения, что E_p » E s , получается зависимость усилия от деформации:

F =

4 E s R 32

3 ( 1 -v 2 )⁵

Путем аппроксимации экспериментальной кривой F ( 5 ) можно найти неизвестную величину модуля упругости материала. Применимость (1) ограничивается размерами острия зонда — при глубине индентации 5> 2 R точность его аппроксимации в виде сферы падает [14], и соотношение (1) дает некорректные результаты. С другой стороны, малая индентация ( 5 <  20 нм) часто нестабильна и может привести к существенному разбросу результатов, в особенности, если речь идет о мягких полимерных материалах [14]. В связи с этим на практике также используются модели, предложенные И. Снеддоном [15]. В общем случае Снеддон представил усилие F по внедрению твердого тела вращения в виде гладкой функции F = а5 n ( а и n — константы), которое в частности для конуса имеет вид:

F = 2 E s 5 ² tg а/ ( п ( 1 -v ² ) ) ,

для гиперболоида:

F =

E_sa ³ | ₂ E a _S2\f п Г 1 E -—— E ² +— 1 -E² — + arctg — ( 1 -v 2 ) R t     2 ⁽      ) ( 2      Д 2 E 2

_s a ² sfn Г 1 El)

5 = E + arctg,

2 R \ 2       1 2 E 2 JJ

E = ( R cth а)/ a ,

,

где а — угол между высотой и образующей конуса либо гиперболоида; R — радиус сферы, вписанной в вершину гиперболоида.

В 1932 году Р. Брадли [16] предложил выражение для нахождения силы притяжения между двумя твердыми сферами из одинакового материала: F = 4 п wR 1 R ₂ /( R 1 + R ₂ ) , где R 1 и R ₂ — радиусы сфер, w — энергия адгезии на единицу площади. Модель Брадли рассматривает контакт твердых сфер только с учетом сил Ван-дер-Ваальса и при условии, что обе поверхности разделены и не учитываются ни упругие, ни пластические деформации, вызванные силами притяжения. Эта теория стала важной частью развития теории контактного взаимодействия.

В 1934 году Б. Дерягин впервые отметил, что поверхности, приведенные в контакт за счет сил притяжения, должны деформироваться в зоне контакта [17] и сделал предположение, что под влиянием поверхностных сил сфера будет деформироваться согласно теории Герца. Затем, используя чисто геометрический подход, он нашел силу притяжения между сферой и плоскостью в зависимости от расстояния между ними, которая при непосредственном контакте имеет вид:

^F adh =- ^{2 П R}w . ⁽⁴⁾

Уравнение Дерягина (4), называемое аппроксимацией Дерягина, соответствует уравнению Брадли [16].

После опубликования работы Герца в литературе появились свидетельства ее противоречий с экспериментами данными. Например, А. Робертс в 1968 году [18] на примере гладких резиновых сфер и К. Кендалл в 1969 году [19] на стеклянных сферах показали, что при малых нагрузках контактная область была большей по площади, чем предсказывала теория Герца, и стремилась к постоянному конечному значению по мере снижения нагрузки до нуля; при чистых и сухих контактирующих поверхностях наблюдалась сильная адгезия. Однако при больших нагрузках результаты экспериментов оказались близкими к результатам теории Герца. В 1969 году Р. Друтовски [20] обнаружил, что площадь контакта стеклянного шарика с эластомером может превышать предсказываемую теорией Герца. При нулевой нагрузке эта площадь является конечной величиной, а адгезионную силу можно измерить, несмотря на бесконечность напряжений на периферии контактной области, ранее показанную К. Джонсоном [21].

В 1975 году Б. Дерягин, В. Мюллер и Ю. Топоров представили теорию упругого взаимодействия деформируемой сферы и абсолютно твердой плоскости с учетом адгезии [22], получившую в дальнейшем название модели Дерягина - Мюллера - Топорова (ДМТ). Главная особенность этой теории заключается в том, что энергия межмолекулярного притяжения учитывается только за пределами контактной области в случае нормального контакта упругих тел, описываемого теорией Герца (Рис. 2 в ). Контактный радиус и глубина индентации рассчитываются здесь по формулам:

a =

Г 3 R ( F + 2 п Rw ) Y^/3

I   4Ё   J

a ²

и 5 = —

R

9 ( F + 2 п Rw ) 2

^ 16 R ( E * ) 2 ^

.

Таким образом, при нулевой нагрузке, в отличие от модели Герца, в модели ДМТ контактный радиус и деформация не равны нулю. Полагается, что модуль упругости сферы настолько велик, что сила молекулярного притяжения не изменяет форму сферы за пределами кольцевой контактной области. Внутри контактной области действуют только сжимающие напряжения; за ее пределами сжимающие напряжения существуют лишь в непосредственной близости к ней. Подстановка а в 5 дает полное усилие, действующее на сферу: F = F_Herz + F_adh , где F_Herz — усилие из решения задачи Герца (1), (2) или (3); F_adh — сила адгезии, определяемая по формуле (4). При использовании модели ДМТ значение контактной площади может быть заниженным из-за того, что геометрия контакта соответствует теории Герца [23]. При нахождении модуля упругости на основе модели ДМТ и АСМ-эксперимента за основу берется кривая обратного хода, а сила адгезии соотносится с наименьшим (максимальным по модулю) усилием при разгрузке.

Следует отметить, что при нулевой деформации материала, например, при надавливании достаточно мягкого зонда на твердую поверхность, справедливо тождество: F = F_adh . В этом случае появляется возможность вычислить поверхностную энергию материала, если прибегнуть к дополнительным методам и моделям [24].

Несколькими годами ранее, в 1971 году, К. Джонсон, К. Кендалл и А. Робертс представили свою теорию контактного упругого взаимодействия — теорию ДжКР [25]. Она также базируется на модели Герца, но учитывает силу адгезии, действующую только внутри области контакта (Рис. 2 в ). Сжимающие напряжения отмечаются только в центре контактной области, растягивающие напряжения — по мере приближения к краю контактной области и стремятся там к бесконечности. При этом модель Герца является частным случаем этой модели при отсутствии адгезионных сил.

Сила адгезии в модели ДжКР имеет вид: F adh = - 1,5 п Rw, а радиус области контакта и глубина индентации соответственно:

a

3 R ( F + 3 п Rw + ^ 6 п RwF + ( 3 п Rw ) ² 4 E ^*

, а2 п wa и 5 =   - 2

R 2 E ^*

.

Для того чтобы с помощью (5) найти модуль упругости материала из эксперимента, можно использовать

некоторые особые точки АСМ-кривой. Как показано на рисунке 3, авторы [26] выделяют четыре точки

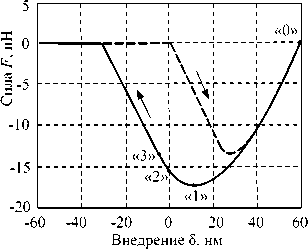
Рис. 3. Силовая кривая АСМ (пунктирная линия – прямой ход, сплошная линия –

на ветви обратного хода и вычисляют модуль упругости образца по сочетаниям значений пары точек, одна из которых « 0 ». Например, при комбинации « 0 » и «1 » —

E s = F 1 ( 1 - v 2 )/^3 R 5 0 , при комбинации « 0 » и « 2 » —

E s = 3 F ₂ ( 1 -v 2 ) /S^R ^ , F и F ₂ — значения сил

в точках «1 » и « 2 » соответственно.

Более точную аппроксимацию можно построить при замене сферы гиперболоидом. В этом случае:

F = 2 E * ]-^

a ²

-

2 R

4 2 fn . ( ^a /4J 2 ^{- 1} ) + arcsin-

1 ²           ( al 4 1 ) 2 + 1 J]

- a

2 а п w

E ^*

обратный ход); в выделенных точках « 0 » – приложенная сила F = 0 ; «1» - сила адгезии F_adh максимальна; « 2 » – глубина индентации 5 = 0 ; « 3» - отделение зонда от поверхности

5= 0 41.

2 R

п

—+ arcsin

( a /41 ) 2 - 1 ' ( a / 4 1 ) 2 + 1 ,

-

2 a п w

E ^*

где ^ 1 = R ctg a . Как и в случае со сферой, при совместном рассмотрении особых точек силовой кривой можно записать выражения для вычисления модуля упругости.

В 1977 году Д. Табор [27] показал, что теории ДжКР и ДМТ представляют собой два экстремума одной адгезионной теории. Рассмотрев взаимодействие двух сфер, он предложил параметр T (параметр Табора),

) ( Rw 2/ ( E1 ) ,

зная который, можно судить о применимости той или иной модели: T = (1/ z 0

где z ₀ — равновесное расстояние между атомами взаимодействующих поверхностей, значение которого обычно лежит в диапазоне 0,3...0,5 [28]. Если T » 1, то предлагается обращаться к модели ДжКР, если T « 1 — к модели ДМТ [29].

Двухточечный метод (при комбинации точек « 0 » и «1 », см. Рис. 2) в рамках теории ДжКР не всегда работает корректно [30]. Данные для вулканизированной резины (полидиметилсилоксана и изобутиленизопрена), найденные экспериментально при разных скоростях нагружения, показали, что не все аналитические решения имеют хорошее согласование с экспериментальными данными. Этот феномен авторы объясняют с помощью параметра T . Оказалось, что там, где обнаруживается расхождение теории и экспериментальных данных, параметр Табора значительно превышает единицу, что означает невозможность применения теории ДжКР [27].

В 1992 году Д. Маугис показал, что модели ДжКР и ДМТ являются предельными случаями еще одной теории [31], впоследствии названной моделью Маугиса. Он предложил рассматривать упругую деформацию двух тел как функцию одного параметра X и использовать для изучения контактного взаимодействия подход, похожий на теорию удара (трещины) Д. Дагдейла [32]. В соответствии с теорией Маугиса контакт происходит по круговой области, и для того чтобы определить деформацию и контактный радиус, необходимо решить последовательность из семи параметрических уравнений. Теория Маугиса экспериментально верифицирована М. Лантцем и другими [33]. Имеется работа, в которой предполагается, что сила трения прямо пропорциональна контактной площади, и в этом случае результаты получаются близкими к аппроксимации Маугиса [34].

Для анализа контакта сферического зонда и плоского образца с образованием большой контактной области можно выбрать модель Маугиса. Выражения для нахождения деформации и силы представлены ниже [26]:

* | R + a ² R + a

F = 2 aE -----In----

I 4 a    R - a

R   /2 a n w

--. I------------------------------------ 2 E ^*

5 = a In

R + a

R - a

-

2 n aw

E ^*

.

Далее, аналогично проделанному ранее, следует рассмотреть особые точки экспериментальной кривой и их комбинации (Рис. 3).

• 2.2.    Динамические взаимодействия зонда с поверхностью

Уравнение вынужденных колебаний массы m на пружине имеет вид:

z + ( to ₀ ]Q ) z + to 0 z = © 0 P cos © t .

Здесь: точка над символом означает дифференцирование по времени; P — амплитуда и ω — угловая частота колебаний вынуждающей силы; to ₀ = k/m — собственная частота колебаний кантилевера, характеризуемого жесткостью k ; Q = to ₀ m/n — добротность системы ( n — коэффициент затухания), величина, показывающая качество колебательной системы, то есть во сколько раз энергия, запасенная системой, больше потерь за один период колебаний. Добротность кантилевера в значительной степени зависит от среды, в которой производятся измерения: ~ 10⁴ при работе в вакууме, ~ 10 3 для воздуха и ~ 10...100 для жидкости.

Решением уравнения (6) служит функция z ( t ) = A cos ( to t -ф ) , которая определяет первую гармонику колебаний зонда. Амплитуда и фаза вынужденных колебаний вычисляются по формулам:

A (to) =

to 2 P

( to 0 -to ² ) 2 +to 0 to ² / Q²

ф ( ю ) = arctg

m to ₀ to

Q ( k - m to ² )

Вследствие близости к поверхности образца изменяются свойства колебательной системы. В первом приближении можно считать, что силовые взаимодействия зонда с образцом увеличивают жесткость кантилевера на величину к 1 [35]: ф(to) = arctg|_mto0to/(Q(k + к1 -mto2 ))J . Сдвиг фазы в результате контакта с поверхностью составляет: Аф = п/2 -ф(to0) ® Qk1 /к . Последнее выражение справедливо только при к1 ^ к . В предположении, что упругая деформация поверхности может быть описана в рамках модели Герца внедрения сферы в плоскость, добавочную жесткость можно найти (см. [35]) как к1 = к (a)E*, где к — константа со значениями от 1,9 до 2,4, ^Д — средний радиус контакта при колебательном режиме. Таким образом, сдвиг фазы при взаимодействии с поверхностью зависит от приведенного модуля упругости:

Аф = к ( a)E* Q/к .

На сдвиг фазы влияют и динамические характеристики зонда и вынуждающей силы. Кроме этого, выражение (7) не учитывает влияние адгезионных взаимодействий, поэтому его применение для количественного определения модуля упругости затруднительно. В целом можно говорить о том, что мягкие материалы, по сравнению с жесткими, дают более высокую разность фаз — в них зонд проникает на бóльшую глубину, и радиус контакта выше.

В силу вязкоупругих и адгезионных свойств материала контакт зонда с поверхностью сопровождается диссипацией энергии [36]: E ds = ( п кА 0 A^Q ) ( sin ф-to A /( to ₀ A 0 ) ) , где to — частота внешних колебаний; A 0 , to ₀ — амплитуда и резонансная частота кантилевера вне контакта с поверхностью; A — амплитуда колебаний при контакте. В случае статического контакта энергия диссипации вычисляется как площадь между кривыми прямого и обратного хода зонда. Если исследуемый материал обладает только упругими свойствами, то есть обратный ход зонда может быть точно аппроксимирован моделями ДМТ или ДжКР, то вся энергия диссипации имеет адгезионную природу. Иначе, площадь между экспериментальной и модельной кривыми даст вязкую составляющую энергии. Применение данного подхода продемонстрировано в работе [37]. Другие авторы [38] для разделения E_dis на составляющие предлагают прибегать к численному моделированию.

Изучение вязкоупругих свойств материала методами АСМ в широком диапазоне частот нагружения выполнено японскими учеными [39] в 2013 г. Для этого АСМ был дооснащен пьезоэлектрическим генератором колебаний и специальной программой управления. Диапазон частот колебаний варьировался от 1 Гц до 20 кГц при амплитуде ~ 5 нм (глубина индентации при этом составила ~ 60 нм). Запуск колебательного процесса происходил только при контакте зонда с материалом. Используя модель ДжКР для определения площади контакта зонда с материалом, авторы вычислили упругую и вязкую составляющие комплексного модуля бутадиен–стирольных и изопреновых вулканизатов, показав удовлетворительное совпадение с макроскопическими испытаниями на динамическом механическом анализаторе (ДМА).

Несмотря на то что реальный зонд АСМ отличается от сосредоточенной массы на пружине, исследования показали, что вклад высших мод в колебания реальной балки с распределенной массой на 2...3 порядка меньше основной гармоники. Однако это утверждение справедливо только для измерений на воздухе (вакууме) при Q = 100...1000. В жидкости, когда добротность системы падает, высшие моды колебаний начинают играть существенную роль [40].

• 3.    Континуальное представление зонда

В случае континуальной модели дифференциальное уравнение изгибных колебаний балки можно записать в виде:

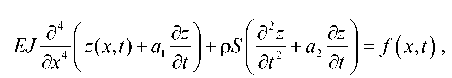
где z ( x , t ) — вертикальное перемещение центральной линии; E , р — модуль Юнга и плотность материала; a ₁ и a ₂ — коэффициенты, характеризующие затухание колебаний ( a ₁ связан с вязким трением внешней среды, a ₂ пропорционален жесткости балки и отвечает за внутреннее трение); J — момент инерции сечения; S — площадь поперечного сечения; f ( x , t ) — внешняя нагрузка. Масса острия считается пренебрежимо малой. Решение данного уравнения зависит от граничных условий и подробно рассмотрено в курсе аналитической динамики [41]. В случае свободных колебаний и отсутствия сил сопротивления рассматриваемое уравнение сводится к следующему:

д ⁴z      д ² z

EJ    + p S    = 0 .

дx4      д t1

Для балки с одним жестко закрепленным концом граничные условия имеют вид:

I -n   д z

^Z'x = ⁰     , дx

= 0 —

x = 0

на закрепленном конце отсутствуют перемещения и повороты;

д ² z

д ² x

= 0 z

’ д ³ x

= 0 — на свободном

конце отсутствуют моменты и сдвиговые усилия; L — длина балки.

Решение упрощенного уравнения представимо в виде: z ( x, t ) = u ( x ) ф ( t ), где u ( x ) определяет форму

колебаний и состоит из бесконечного числа отдельных гармоник:

cosk L + chk L

U - ( x ) = ( cosk - x - chk - x ) -      -        - ( sink - x - shk - x ) ( n = 1,2,3,...),               (8)

sink L + shk L nn

где k - — волновые числа: k 1 L = 1,875, k 2 L = 4,694, k _;.L = ( i - 1/2 ) п при i >  2. Угловые резонансные

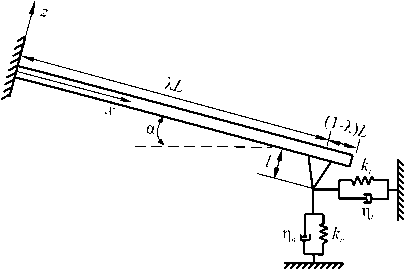
Рис. 4. Схема модели кантилевера как сплошного упругого балки; k_n и k _t – контактная жесткость в нормальном и латеральном направлениях, п - и П t — вязкость в нормальном и латеральном направлениях

частоты колебаний находятся по формуле: to _n = k-^EJ p sS . Решения для более сложных случаев (при внешнем гармоническом возбуждении, колебаниях вблизи поверхности материала) рассмотрены в [42, 43]. В работе [42] проведено экспериментальное исследование мод свободных поперечных колебаний балочных кантилеверов; результаты показали хорошее совпадение с решением (8).

При изучении движения кантилевера с малой амплитудой колебаний около положения равновесия используется линеаризованная математическая модель с двумя элементами (Рис. 4) [44]. Один элемент, изображенный на рисунке в виде пружины, отвечает за перемещение кантилевера как упругого тела, второй — вязкий, соответствует демпфированию [42, 45–47]. Если предположить, что зонд расположен на конце балки ( Х = 1), то граничные условия можно представить в виде:

д z

^Z' x = ⁰     ,    дx

= 0, x=0

EJ дx2

= F, ■ I, EJ \z дx3

-F n,

где l — высота зонда, F_lat и F_n — латеральная (действующая в плоскости, перпендикулярной оси z ) и нормальная (действующая в плоскости, проходящей через оси x , z ) силы соответственно.

В граничных условиях (9) в качестве нормальной ( F_n ) и латеральной ( F_lat ) сил можно взять выражения из моделей Герца, ДМТ или ДжКР. Например, если обратиться к модели ДМТ, то нормальная сила взаимодействия выглядит (см. [44]) как

F - =

- HR, ( 6 5 ² ) , 5> a ₀;

- HR /( 6 a 0 ² ) + 4 E * V R ( a 0 - 5 ) ^3/2/з - п - ( a 0

-5 ) ^1/2 5 ,

5< a 0 ,

где H — постоянная Гамакера; R — радиус скругления зонда; 5 — расстояние между зондом и поверхностью образца; a ₀ — межмолекулярное расстояние.

Согласно теории Герца латеральная сила выражается следующим образом [44]:

[ 0, 5> a ₀ ;

F , = <               ,-------- .

8< a 0 ,

lal 1-8 GRRTO/^S 5 la, -п lat 5 lat, где 5lat — относительное перемещение в латеральном направлении; G* — эффективный модуль сдвига.

В случае нелинейного контакта Герца предлагается применять метод “multi-scales” [48], а также численные методы, в частности, метод конечных элементов [49, 50].

• 4.    Численные модели взаимодействия

• 5.    О практическом применении моделей

  Первая работа, связанная с определением упругих свойств исследуемого материала методами АСМ-микроскопии, была выполнена в 1989 году [59]. Авторы, используя модель Герца, установили модуль упругости по экспериментальным данным для эластомеров, графита и золота. Результат имел достаточно хорошее согласование с литературными значениями.

Помимо рассмотренных ранее аналитических моделей взаимодействия зонда АСМ с образцом для расшифровки экспериментальных данных могут применяться численные модели. Чаще всего используется метод конечных элементов (МКЭ) и методы молекулярной динамики (методы МД), а также, для некоторых подзадач, — метод Галеркина и метод Рунге-Кутты.

Метод конечных элементов хорошо подходит для решения контактных задач внедрения зонда в поверхность образца. При этом по полученным результатам можно оценить не только возникающие при контакте упругие силы, но и адекватность модели контактного взаимодействия, заложенной в расчет. Так, с помощью МКЭ было установлено, что если глубина внедрения зонда в образец не превышает 0,4 радиуса его скругления, то зависимость упругой силы от глубины проникновения, рассчитанная по формуле Герца для линейно упругого материала, совпадает с численным нелинейно-упругим (нео-гуковым) решением [51]. Если поверхность образца содержит неровности, соизмеримые с размером острия зонда, то прямое применение вышеперечисленных моделей невозможно (изменяется площадь контакта). В этом случае также целесообразно обращаться к МКЭ. Численные расчеты показывают, что зависимость сила–глубина проникновения зонда сильно зависит от места его внедрения [52]: в вершину выпуклости, в ее основание или в промежуточную область.

Другим примером использования МКЭ является исследование слоистых материалов (тонких покрытий, клеточных оболочек и тому подобных) при малой толщине покрытия, когда свойства нижележащего материала (подложки) оказывают влияние на результаты. Так, в работе [53] на основе экспериментальных данных и МКЭ-вычислений установлено влияние углеродной подложки на жесткость покрывающих ее полимерных нанослоев (экспериментальная модель межфазных слоев в наполненном вулканизате). В другой работе [54] авторы приводят результаты экспериментально-теоретического анализа межфазных слоев, окружающих частицы наполнителя в вулканизате, однако проведенные вычисления не учитывают кривизну поверхности этих частиц.

Метод конечных элементов применяется также: при моделировании движения кантилевера под действием нормальных и латеральных сил [6, 44] (полученные результаты используются для калибровки кантилевера); для определения силы трения между зондом и образцом [49]; для объяснения характерного скачка на силовой кривой при подводе зонда к поверхности [55].

Методы континуальной механики (МКЭ, аналитические модели) эффективны только в тех случаях, когда размеры рассматриваемой области во много раз больше межатомного расстояния. В противном случае используются методы МД. В молекулярной динамике материалы зонда и образца заменяются системой шариков — атомов, взаимодействующих при помощи энергетических потенциалов. Методы МД требуют больших временных затрат при вычислениях, поэтому они оказываются удобными при исследовании взаимодействия небольшой области зонда и образца: при изучении трения кончика зонда о поверхность [56], при вычислении энергии адгезионных взаимодействий [57] или моделировании полуконтактного динамического режима работы АСМ [58]. Скорость и результаты расчета с помощью методов МД зависят от выбора потенциала межатомного взаимодействия. Важным фактором являются условия проведения эксперимента, а следовательно, и «среда» проведения расчетов МД. Идеальны для моделирования условия вакуума, когда поверхность образца не покрыта нанослоем адсорбировавшейся из воздуха жидкости.

С тех пор опубликованы и продолжают публиковаться работы как согласующиеся с моделями, так и указывающие на границы их применимости. Критерием работоспособности аналитической модели в каждом конкретном случае является совпадение результатов либо с численным моделированием, либо с макроскопическими испытаниями. Следует указать некоторые факторы, затрудняющие использование рассмотренных моделей. Это:

– неупругие взаимодействия «зонд–образец», часто возникающие при изучении полимеров и выражающиеся в несовпадении прямого и обратного хода кантилевера (участки CD и DE на рисунке 1). Если задача заключается в определении упругого модуля, то данная проблема может быть решена путем увеличения скорости движения зонда при индентации;

– качество поверхности — в зоне индентации она должна быть как можно более плоской (ортогональной к ходу зонда по оси z ) и менее шероховатой. В противном случае нарушается гипотеза, заложенная в рассмотренные модели, согласно которой область контакта представляет собой сплошной круг. При индентации наклонных поверхностей возможно проскальзывание зонда; при шероховатых — смятие, либо хрупкое разрушение рыхлой структуры поверхности, что приведет к завышению глубины индентирования, и следовательно, занижению модуля упругости;

– механические и геометрические особенности кантилевера и острия зонда; реальная жесткость зондов k может значительно отличаться от той, которую указывает производитель. Перед проведением количественных измерений необходимо всегда производить калибровку жесткости. В случае аппроксимации зонда сферой требуется следить за тем, чтобы глубина индентации не превышала 2 R ;

– наличие нанослоя адсорбированной жидкости; любая поверхность при комнатных условиях покрыта таким слоем, и его толщина зависит от температуры, влажности и гидроскопических свойств поверхности. При подводе зонда к образцу в результате капиллярных явлений происходит неконтролируемый скачок зонда по направлению к поверхности. Если материал достаточно мягкий, то это приведет к дополнительной индентации. Данный нанослой вносит вклад в адгезионные взаимодействия. Во избежание проблем, связанных с этим слоем, механические испытания на АСМ можно проводить в жидкой среде (воде), либо в вакууме;

– другие факторы, как то: близость подложки при исследовании свойств нанопокрытий; возникновение на поверхности особого нанослоя в результате воздействия внешней среды или диффузии текучих компонент из объема; повреждение мягких образцов, например, прокалывание клеточных оболочек, и прочего.

Заменой аналитическим моделям служат методы конечно-элементного моделирования и молекулярной динамики. Однако моделирование эксперимента на их основе является отдельной трудоемкой задачей, требующей введения дополнительных гипотез о неизвестных априори свойствах материала на наноуровне. Таким образом, несмотря на все существующие проблемы и ограничения, рассмотренные аналитические модели в силу своей простоты активно используются на практике при определении модуля упругости на локальном субмикронном уровне материала.

Работа выполнена при финансовой поддержке РФФИ (проект № 14-01-96002), Министерства образования и науки Пермского края (соглашение № С-26/627), Программы фундаментальных исследований УрО РАН (проект № 12-Т-1-1004).