Определение местоположения объекта с использованием улучшенной трехточечной пассивной системы

А нализ исследований в области пассивной координато-метрии [1 – 7] позволяет выделить основные направления дальнейшего развития:

• ♦    определение координат объекта поиска (с учетом сферичности фронта распространения волны), обеспечивая уменьшение систематической погрешности;

• ♦    уменьшение неопределенности полученных координат объекта при решении системы нелинейных уравнений, описывающих его движение, исключение грубых промахов.

Как показывает опыт, для решения этих задач целесообразно применять разностно-дальномерный метод (РДМ) определения координат, в основе которого лежит измерение разности дальностей до пары точек приема (ТП). При этом имеются следующие особенности:

• ♦    используются пассивные точечные средства поиска (СП) или приемники, например, сейсмические;

• ♦    отсутствует априорная информация о параметрах сигнала и координатах объекта;

• ♦    определение координат обеспечивается для всех точек зоны чувствительности СП;

• ♦    возможна инвариантность топологии ТП на местности.

Общий алгоритм РДМ по определению местоположения предполагает отыскание корней системы нелинейных урав- нений, которые связывают ТП ‒ места установки СП (типично 3) с координатами объекта. Решение уравнений является сложной задачей, обычно не имеющей точного аналитического вывода. Из известных моделей РДМ, по мнению авторов, наиболее рациональным является пеленгатор Сайбеля, в котором в определенной степени устраняется неоднозначность определения координат объекта на линии пеленга за счет решения системы нелинейных уравнений гипербол [3]. Данная статья направлена в развитие этого метода.

Пусть в системе координат xOy линии гипербол заданы системой уравнений (1), описывающей положение объекта локации при использовании 3-х приемников с произвольной топологией ( рис. 1 ). Местоположение объекта (т. D ) определяется системой уравнений линий гипербол [3] и представляется в виде линии пеленга:

a1x2 + b1y2 + f1 = 0;

a2x2 + b2y2 + c2xy + d2x + + e2y + f2 = 0; (1) a3x2 + b3y2 + c3xy + d3x + e3y + f3 = 0, где an, bn, fn (n = 1, 2, 3): cm, dm, em (m = 1, 2) – параметры гипербол, связывающие неизвестные значения координаты т.D (объект) с известными координатами тт. А, В, С (ТП) и измеренными значениями разностей дальностей ∆rAB, ∆rAC, ∆rBC.

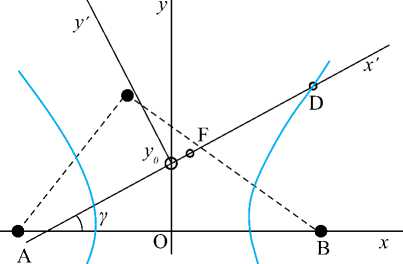
Рис. 1. Задача по определению координат объекта

Система уравнений (1) рассматривается как базовая модель для получения 3-х линий пеленга при использовании 4-х приемников, решения – суть несколько корней (до 4-х), среди которых есть истинные координаты объекта т. D . Для их определения достаточно использовать 3 приемника, вычисляя разности дальностей до объекта, на их основании строя линии гипербол и линию движения (пеленга) объекта локации. Пусть эта линия пересекает ось Ох под углом γ (пеленг объекта) и проходит через точку наблюдения F(x_F, y_F) , имеющую координаты:

y = y 0 + x×tgγ , (2)

где y₀ – ордината пересечения линией пеленга оси Оу .

Найдем координаты точки, являющейся пересечением линии гиперболы и прямой. При одновременном перенесении начала системы координат в точку Y₀(0,y₀) и повороте координатных осей на угол γ ( рис. 1 ), система уравнений (1) представима в виде:

Таким образом, на основе РДМ и с учетом технического решения [3] разработана модель определения координат объекта в виде уравнений (4 – 6). Модель позволяет получить точное аналитическое решение системы гиперболических уравнений определения координат объекта триадой приемников при отсутствии итерационных процедур (которые делали ранее невозможным обработку значительного потока данных в масштабе реального времени). При этом снято ограничение на топологию ТП и применен пеленг, однозначно определяющий местоположение объекта.

Это позволяет найти точки пересечения линии пеленга и линии гиперболы, что отличает эту модель от известных, где местоположение рассматривается как пересечение двух гиперболических линий. При этом с 4 до 2 уменьшено количество точек возможного местоположения объекта по сравнению с известными методами определения координат в [5, 6]. Решениями уравнения (4) являются два значения дальности, из которых одна – истинная. На рис. 2 показана неоднозначность при определении координат объекта – обе точки D1 , D2 являются решениями (3). При этом в зависимости от топологии триады ТП и величины пеленга возможно определить одно истинное значение дальности.

Например, для прямоугольной равнобедренной топологии при условии, что расстояние от точки наблюдения до объекта значительно превышает базу триады, т.е. L₁ , L₂ > a , то угол пеленга γ ≈ ±45˚ является границей перехода определения дальности по показателю L₁ к показателю L₂ при положительных значениях пеленга. Полученное значение дальности (от точки наблюдения) для малобазовых систем поиска практически совпадает с дальностью до объекта из центра координат. При определенном пеленге на объект, находящийся на расстоянии, значительно превышающем базу а , однозначное решение координатометричной задачи находится путем сопоставления угла пеленга с секторами определения дальности.

При нахождении объекта вблизи триады ТП ширина сектора определения параметров L₁ или L₂ существенно изменяется, что приводит к необходимости уменьшения неоднознач-

(x’)² (acos²γ – sin²γ) – (x’)²y₀ sinγ – y₀² + f₁ = 0 .       (3)

Выражение (3) позволяет в системе координат x’O’y ’ определить координаты точки пересечения линий положения объекта при условии x’ = L и получить уравнения, описывающие координаты объекта. Расстояние от точки наблюдения (пересечения пеленгом оси ординат Y₀(0, y₀) ) до объекта есть:

_ y₀ siny ± Ajy₀ sin у — (a_x cos" у — sin у)(— y₀) .

(a, cos у - sin у)

Угол пеленга объекта

γ = arctg((2a×∆rAC – (a + x3)×∆rAB)/(y3×∆rAB)),        (5)

где a = |AB|×½ – база точек приема; x₃, y₃ – координаты точки приема C( x₃, y₃ ).

Ордината пересечения линии пеленга и оси ординат yn - У, хДеу - ^ + Гдс X Гдв "" Г4С "" a .              (6)

Ун AFvbi

2y3

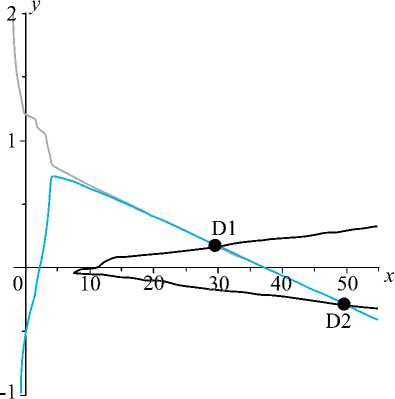
Рис. 2. Неоднозначное определение дальности до объекта

ности решения. Например, характерным является наличие двух решений при пеленге на объект (с центра координат) в интервалах –30…0 и 60…90 град. Следует отметить, что значения L₁ или L₂ могут быть со знаком минус, что указывает на нахождение объекта во II или III координатном углу.

Поскольку физическая природа параметров мощности и разности дальности ‒ разная, возможно составить уравнение для оценки, например, параметра радиуса окружности линии положения объекта L_p , при этом в уравнение будут входить показатели времени и мощности сигнала. При этом в соответствии с рис. 3

i?„=(X-xcy+Y;,

где Xj , L_p – абсцисса центра и радиус окружности как линии положения объекта, определенные по параметру мощности сигнала в двух точках приема [4]:

^P р„-р_ь ’ ' P„-P_b

где P_a , P_b – мощности принятого сигнала двумя разнесенными точками приема A (– a ,0), B ( a ,0).

Рассмотрим дополнительно измерение параметра мощности сигнала в 2-х ТП. Координаты объекта связаны с расстоянием L₁ или L₂ , полученными по (4), выражениями

По критерию (11) выбираем одну из дальностей, для которой квадрат разности расстояний будет наименьшим, – это значение и будет истинным, а решение – однозначным.

Таким образом, улучшенная трехпозиционная пассивная система определения координат объекта обеспечивает:

• 1)    определение пеленга триадой ТП произвольной топологии (2 решения);

• 2)    выбор искомого решения как координаты точки пересечения линий гиперболы и пеленга, которые являются линиями положения объекта;

• 3)    инвариантность расчетов к топологии точек приема;

• 4)    комплексное измерение временных и амплитудных параметров сигнала.

При этом регистрируемыми параметрами являются мощность сигнала и величины временной задержки распространения волны между ТП.

Описанная система поиска отличается от известных тем, что снимаются ограничения на топологию 3-х ТП, а полученные аналитические зависимости обеспечивают однозначное определение координат за счет комплексного контроля временных и амплитудных параметров сигнала. Использование этого «улучшенного» РДМ позволяет повысить эффективность контроля перемещения объектов, в том числе допускает инвариантность топологии точек приема, и исключает грубые промахи из-за имевшейся ранее неоднозначности определения координат ■

Xc = L1(L2)cosγ, Yc = y0 – L1(L2) sinγ.

Истинным будет такое значение L₁ или L₂ , при котором различие между определением показателя L_p по параметрам мощности и разности дальностей будет минимальным:

^1 = |^ - (^xi - ^L^ ^cos( У)² - (A ^sin(У) + Vo )²1           (9)

N₂ =\l²„- (X, - Z₂cos(7)²- (Z₂sin(7) + _Jo)²| ,         (10)

где N₁ , N₂ – модуль разности квадратов радиусов окружностей как линий положения объекта, определенных по параметрам времени и мощности.

Критерием однозначности определения координат будет решение системы:

L_t при N_t<  Nt, L, при N, < N_v

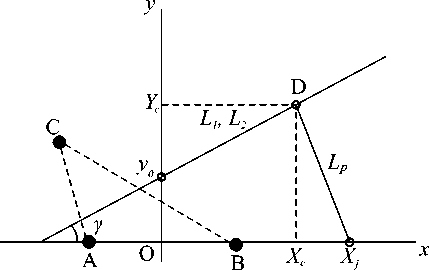
Рис. 3. Однозначное определение координат объекта