Определение модельных констант при вычислении температуры плавления ДНК

Известно, что генетическая информация закодирована в ДНК в виде двух полимерных цепей, соединенных водородными связями. Цепи образуют двойную спираль, содержащую азотистые основания-нуклеотиды: аденин (A), гуанин (G), тимин (T) и цитозин (C).

Согласно правилу комплементарности нуклеотиды A и G первой цепи связаны соответственно с нуклеотидами T и C второй цепи [1].

Физический процесс плавления молекулы ДНК возникает при повышении температуры и связан с переходом "спираль — клубок". Термодинамическая теория перехода ДНК "спираль — клубок" основана на учете разности свободных энергий спирального и клубкообразного состояний [2]. Процесс плавления сопровождается значительным изменением физических свойств исследуемого раствора ДНК, позволяющим проводить анализ: поглощение в ультрафиолетовой части спектра (260 нм) возрастает на 30–40 % [3], а вязкость раствора снижается в 12 раз [4].

Современный метод анализа кривых плавления молекулы ДНК реализуется на анализаторах нуклеиновых кислот после ПЦР в реальном времени с применением флуоресцентных красителей, интенсивность которых может изменяться более чем в 100 раз [5]. При этом получаются кривые плавления продуктов амплификации, представляющие собой зависимость измеренной величины флуоресцентного отклика от температуры образца. При вторичной обработке каждой кривой плавления определяется температура плавления ДНК Tm как точка перегиба этой кривой. Значение температу- ры Tm соответствует энергетическому состоянию, при котором половина молекул ДНК находится в спиральном, а другая половина — в клубкообразном состоянии [3].

Температура плавления T m зависит от состава фрагмента ДНК, это объясняется энергетическим состоянием ДНК: в паре нуклеотидов GC имеются три водородные связи, в паре АТ — только две. Поэтому чем больше пар GC в ДНК, тем более она "тугоплавка" [6]. В 1962 г. на основе анализа нескольких десятков образцов [7] была выявлена линейная зависимость между температурой T m и содержанием GC-пар нуклеотидов [G + C]:

T m = 69.3 +0.41[G + C], (1)

где [G + C] — содержание нуклеотидов G и С в продукте ПЦР (%). В этой и следующих моделях константы имеют единицы измерения, обеспечивающие единство размерности всех слагаемых в этих моделях.

На значение температуры T m оказывают влияние и другие факторы: например, температура плавления фрагмента ДНК обратно пропорционально зависит от длины этого фрагмента [8, 9] и является линейной функцией логарифма концентрации ионов металлов в анализируемом растворе [10, 11]. Эти факторы учтены в следующей модели [12]:

T m = 81.5 + 16.6 lg ([K⁺]) +

+ 0.41 [G + C] – 675 / L p , (2) где [K⁺] — концентрация ионов калия (моль/л); L p — длина продукта (пар нуклеотидов, п. н).

Известна программа Tm_Tool [13] для расчета температуры плавления ДНК. В описании программы представлено следующее уравнение для последовательностей ДНК, длиннее чем 50 п. н., при pH раствора от 5 до 9:

T m = 81.5 + 41 (yG + zC) / (wA + xT + yG + zC) – – 500 / (wA + xT+ yG + zC) + +16.6 log 10 ([Na⁺]) – 0.62 F ,                 (3)

где yG, zC, wA и xT — количество соответствующих нуклеотидов; [Na+] — концентрация в растворе ионов натрия (моль/л); F — процентная концентрация формамида (%). Видно, что увеличение концентрации формамида линейно снижает температуру T m [14].

Температура плавления зависит также от pH среды, значительно снижаясь при значениях pH ниже 5 и выше 9, что связано с эффектами протонирования и депротонирования азотистых оснований в кислой и щелочной средах [15]. Существенно на значение T m влияют тип и концентрация флуоресцентного красителя. Так, изменение температуры плавления может достигать (0.7 ± 0.1)°C при использовании красителя SYTO-64 и (10 ± ± 0.02)°C при использовании красителя SYBR Green I [16]. Зависимость интенсивности флуоресцентного отклика свободного красителя от температуры [17] также может влиять на значение температуры T m .

Зависимость температуры T m от некоторых из описанных выше факторов является линейной только при неизменных других факторах. Например, концентрация формамида может изменять температуру T m в диапазоне 2.4–2.9 ºC/моль в зависимости от содержания GC-пар нуклеотидов [G + C] [14]. Такая зависимость значительно усложняет модель для вычисления температуры плавления ДНК.

Существующие модели не учитывают всех факторов, влияющих на величину температуры плавления ДНК, погрешность вычисления темпе- ратуры Tm превышает 1 °C, что является неприемлемым для большого количества прикладных задач [18, 19]. Таким образом, существует необходимость создания новых моделей, позволяющих более точно определять значение температуры Tm при изменении некоторых факторов, например длины фрагментов ДНК и содержания GC-пар нуклеотидов, и неизменных иных факторах.

ПРИМЕР МОДЕЛИРОВАНИЯ ЗАВИСИМОСТИ ВЕЛИЧИНЫ T m ОТ ДЛИНЫ ФРАГМЕНТОВ ДНК И СОДЕРЖАНИЯ GC-ПАР НУКЛЕОТИДОВ

Формулы (2) и (3) можно представить в виде упрощенной модели, учитывающей изменение значений длины фрагмента ДНК L p и содержания нуклеотидов [G + C], справедливой для экспериментов с неизменными прочими параметрами:

T mc = P1+ 0.41 [G + C] – P2 / L p .          (4)

Здесь исходное значение P1 при постоянном составе среды равно сумме 81.5 + 16.6 lg [K⁺] на основании формулы (2) или 81.5 + 16.6 lg([Na⁺]) – – 0.62 F , на основании формулы (3).

Значения модельных констант P1 и P2 вычисляются на основе данных, полученных в программе Tm_Tool, по методу наименьших квадратов (МНК) [20, 21]. Определяется сумма квадратов отклонений Q модели Tmc от экспериментальных данных Tm :

n - 1                                                       \2

Q = ! ( T mc ( L p , [ G + C ] ,P1,P2 ) - T m ) ,      (5)

i = 0

где n — количество измерений.

Минимум суммы квадратов отклонений Q определяется из условий равенства нулю частных производных функции Q путем изменения коэффициентов L p , [G + C], P1 и P2 .

Табл. 1. Оценка отклонения вычисленного значения T _m

№ фрагмента	L p , п. н.	T °C m ,     , по Tm_Tool	T m , °C, по ф-ле (6) ( T m(6) )	Δ T m
1	100	85.69	85.60	–0.09
2	200	87.59	87.80	0.21
3	400	88.91	88.89	–0.02
4	600	89.28	89.26	–0.02
5	800	89.48	89.44	–0.04
6	1000	89.59	89.55	–0.04

В столбце " T m , °C, по Tm_Tool" табл. 1 представлены значения температуры плавления T m , рассчитанные с помощью известной программы Tm_Tool при содержании нуклеотидов [G + C] = = 50 % в зависимости от длины фрагментов L p .

Формула (4), уточненная в программной среде MatLab с помощью функции regress по значениям T m , L p и [G + C], имеет вид:

T m = 69.5 +0.41 [G + C] – 438.4 / L p . (6)

Для оценки отклонения вычисленной температуры плавления T m по формуле (6) в столбце T m(6) табл. 1 находятся значения, рассчитанные по этой формуле в зависимости от длины фрагментов L p . Значение Δ T m соответствует разности значений " T m по Tm_Tool" и T m(6) .

Максимальное отклонение вычисленной температуры плавления T m по формуле (6) составляет 0.21 °C, значение СКО составляет 0.05 °C. Для оценки адекватности модели, полученной при использовании программы Tm_Tool, необходимо сравнить ее результаты с результатами эксперимента.

ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ЗНАЧЕНИЙ ТЕМПЕРАТУРЫ ПЛАВЛЕНИЯ

ФРАГМЕНТОВ ДНК T M

Исходные (сырые) данные получены методом анализа кривых плавления на анализаторе нуклеиновых кислот АНК-32, который серийно выпускается в Институте аналитического приборостроения РАН (ИАП РАН).

Выполнен трехкратный анализ 3 образцов ампликонов цитокератина (CK-19) в четырехкратном повторении по методике плавления в диапазоне температур образца 70–95 °C с шагом 0.5 °C и длительностью выдержки каждого значения температуры 30 с.

С помощью программы ANK_Melting [22] определены 12 величин T m каждого образца. Вычислены средние значения T m каждого образца: 84.30, 90.42 и 90.55 °C. Погрешность определения средней температуры плавления T m для этих образцов оценена с помощью значения СКО, которое составляет 0.12 °C.

В верхней части рисунка показаны кривые плавления, полученные при анализе трех образцов с разной температурой плавления. В нижней части рисунка показаны производные от этих кривых по температуре.

Средние значения T m для образцов 1, 2 и 3 приведены в столбце T mА табл. 2. Образцы 1, 2 и 3 имеют соответственно содержание нуклеотидов [G + C], равное 53, 59 и 58 % при длине фрагментов L p , равной 103, 209 и 309 п. н. соответственно.

Параметры среды в эксперименте соответствуют параметрам, принятым при расчете значений T m с помощью программы Tm_Tool. Это позволяет оценить соответствие формулы (6) экспериментальным данным. Отклонение вычисленного значения T m образцов 1, 2 и 3 оказалось значительным и составляет 2.60, 1.45 и 1.09 °C соответственно. Для уточнения предложенной модели предлагается определить модельные константы в соответствии с экспериментальными данными.

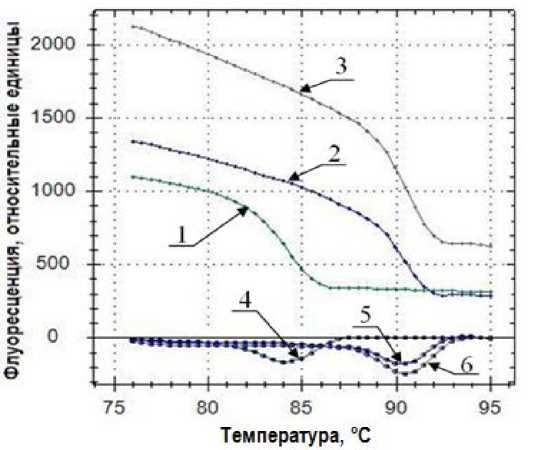
Графики плавления (линии 1–3), полученные при анализе трех образцов, и их производные по температуре (линии 4–6)

Табл. 2. Определение модельных констант P1 и P2

№ образца	[G + C], %	L p , п. н.	T m(7) , °C	T mА , °C	Δ T m
1	53	103	84.37	84.30	0.07
2	59	209	90.14	90.42	–0.29
3	58	309	90.77	90.55	0.22

ОПРЕДЕЛЕНИЯ МОДЕЛЬНЫХ КОНСТАНТ ПРИ ВЫЧИСЛЕНИИ ТЕМПЕРАТУРЫ

ПЛАВЛЕНИЯ ФРАГМЕНТОВ ДНК ПО РЕЗУЛЬТАТАМ АНАЛИЗОВ

Значения модельных констант P1 и P2 формулы (6) вычисляются на основе данных T _mА по методу наименьших квадратов.

Формула, модельные константы которой определены по экспериментальным данным в программе Matlab, имеет вид:

T m = 69.2 + 0.41 [G + C] – 671.8/ L p . (7)

В столбце T m(7) приведены значения температуры плавления T m , рассчитанные по формуле (7) в зависимости от величин [G + C] и длины фрагментов L p . Значение Δ T m в табл. 2 соответствует разности T m(7) – T mA .

Максимальное отклонение вычисленной температуры плавления T m по формуле (7) соответствует значению 0.29 °C, значение СКО равно 0.13°C.

Модель обеспечивает возможность сравнивать исследуемые образцы по экспериментальным результатам определения величин T m . Например, изменение длины фрагмента L p от 100 до 110 п. н. вызывает изменение T m на (671.8 / 100) – – (671.8 / 110) = 0.6 °C, а изменение состава [G + C] на 1 % вызывает изменение T m на 0.41 °C.

ЗАКЛЮЧЕНИЕ

Предложено применение упрощенных моделей для вычисления температуры плавления ДНК T m , учитывающих зависимость от некоторых факторов и справедливых для экспериментов с неизменными прочими факторами. В качестве примера приведена упрощенная модель, учитывающая зависимость от длины фрагмента ДНК и содержания GC-пар нуклеотидов.

Описана методика определения модельных констант для вычисления температуры плавления фрагментов ДНК на основе экспериментальных данных и данных из известных литературных источников.

На анализаторе нуклеиновых кислот АНК-32 проведен трехкратный анализ методом плавления трех известных образцов ДНК с четырехкратным повторением. В результате выполнена оценка погрешности определения средней температуры плавления Tm: значения СКО для этих образцов во всех пробирках — не более 0.12 °C.

Отклонение вычисленной температуры плавления T m при использовании уточненной по экспериментальным данным модели не превышает 0.29 °C, значение СКО составляет 0.13 °C.

Работа выполнена в ИАП РАН в рамках государственного задания № 075-01073-20-00 Министерства науки и высшего образования РФ.