Определение напряженного состояния оболочечных конструкций c применением дискретных рядов Фурье

При решении двумерных краевых задач определения напряженного состояния тонкостенных оболочек в рамках механики оболочек зачастую прибегают к дифференциальным уравнениям в частных производных. Во многих случаях подходы основываются на представлении решения в виде рядов Фурье по одной из координат [1–3]. Это позволяет понизить размерность задачи и свести ее к одномерной, решение которой затем может быть получено с использованием аналитических или численных методов.

Ретроспективный взгляд на применение тригонометрических рядов при расчете оболочек в случаях локальных воздействий нагрузок можно найти в работе [4]. Отметим, что, по-видимому, первые работы по расчету оболочек с помощью рядов провели У. Финстервальдер и Г. Рейснер в тридцатые годы прошлого века [4]. С тех пор вышли сотни работ, в которых решение задач определения напряженно-деформированного состояния оболочек осуществлялось с привлечением различных видов рядов, в том числе и рядов Фурье. И всегда приходилось отвечать на непростые вопросы: как подобрать коэффициенты ряда, наилучшим образом аппроксимирующие необходимые функции; сколько членов ряда необходимо удерживать в решении и другие.

В данной работе подход к нахождению напряженного состояния оболочек основывается на применении дискретных рядов Фурье. При этом напряженное состояние описывается суммой двух независимых функций, каждая из которых представляет собой дискретный ряд Фурье по косинусам и синусам, что позволяет рассматривать произвольный несимметричный случай нагружения конструкции. Проведено сопоставление результатов использования аналитических и дискретных рядов Фурье для определения напряженного состояния изотропных и ортотропных оболочек.

Запись в виде дискретного ряда Фурье становится актуальной в связи с упрощением осуществления решения благодаря развитию вычислительной техники и появлению различных сеточных методов для анализа разного рода элементов конструкций [5–7].

Пусть напряженное состояние упругой оболочки в ортогональной криволинейной системе координат О аР описывается системой дифференциальных уравнений в частных производных [7]:

д Z     ( „

= ^ф i а , ^р , да

V

Z) дрk J

+ f i ( а , Р )

( i , j , k = 1, l ),

где Z i = Z i ( а , в ) ( а 1 < а < а ₂, Р 1 < в < Р ₂) — искомые разрешающие функции; Ф i — функции, линейные относительно своих аргументов; f ( а , Р ) — правые части. Данная система дополняется граничными условиями на контуре а = const. Если оболочки вращения будут замкнутыми в направлении О Р , то граничные условия в этом направлении следует заменить условиями периодичности.

Краевая задача, изображаемая системой (1), позволяет вследствие периодичности всех искомых функций представить их в виде рядов Фурье по координате Р . Однако это осуществимо, если все члены уравнений с соответствующими коэффициентами не препятствуют разделению переменных в этом направлении. Для некоторых моделей оболочек система (1) содержит члены с коэффициентами, зависящими от жесткостных параметров, что делает невозможными разделение переменных и представление искомых функций в виде рядов Фурье, но принципиальных затруднений не создает. В такие системы вводятся некоторые добавки, выражающиеся через разрешающие функции и их производные [7]. При решении прикладных задач в случае тонких оболочек можно использовать либо классическую модель оболочки, либо модели, основанные на других, менее жестких, гипотезах.

2.    Постановка задачи

Исследуем оболочки вращения (в общем случае слоистые и ортотропные) в геометрически и физически линейной постановке. Для описания состояния оболочки воспользуемся уравнениями классической теории, основанной на гипотезах Кирхгофа–Лява. Координатную поверхность оболочки отнесем к криволинейной ортогональной системе О 5 6 , где 5 — длина дуги меридиана, 0 — центральный угол в сечении, перпендикулярном оси вращения z (Рис. 1).

Задача определения напряженного состояния оболочки (1) с переменными вдоль образующей параметрами сводится к системе уравнений в частных производных [2]

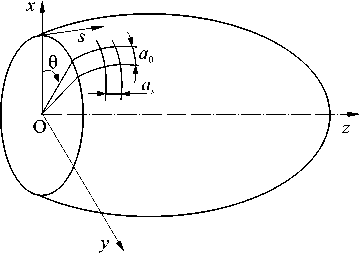
Рис. 1. Виртуальный оболочечный элемент с размерами a_s и a 6 по меридиану и окружности

Y = 1A (5 )^+f (5, 6), д5 tO m ( ) д6m ( )

Y = { N r , N z , . M , U r , U z , v , 9 5 } T ,

где Y — вектор разрешающих функций; Nr , Nz — радиальное и осевое усилия; ur, uz — радиальное и осевое перемещения; Sˆ — сдвигающее усилие; Ms — меридиональный изгибающий момент; v — окружное перемещение; 95 — угол поворота нормали к контуру s . Элементы матрицы Am зависят от геометрических и механических характеристик оболочки, компоненты вектора f — от поверхностных нагрузок.

Все многообразие внешних силовых воздействий можно описать компонентами действующей распределенной нагрузки: касательной к образующей ( q s ), касательной к направляющей ( q ₆ ), нормальной к поверхности ( q _Y ) оболочки, если представить их в виде разложений [2]

от                                                           от                                                          от qs (s, 6) = £ qs (s)cos k6 ,    q6 (s, 6) = £ q6 (s)sin k6,    qY (s, 6) = £ qY (s)cos k6,            (4)

k = 0                                          k = 1                                         k = 0

где k — номер гармоники.

В силу периодичности компонент поверхностной нагрузки все функции, определяющие состояние оболочки, можно разложить в ряд Фурье по окружной координате 6 . Имеем [2]:

- для симметричных компонент вектора разрешающих функций Nr, Nz, Ms, ur, uz, 9s от

Ф ( s , 6 ) = £ Ф ( s )cos k 6 ,                                     (5)

k = 0

– для антисимметричных компонент S , v от

T ( s , 6 ) ^' P ( s )sin k 6 .

k = 1

Разложения (5) и (6) можно использовать лишь при условии, что симметричные компоненты вектора разрешающих функций (3) симметричны относительно вертикальной оси x. При этом угол 6 отсчитывается от оси так, как показано на рисунке 1. Тогда все компоненты вектора (3) раскладываются либо только по косинусам, либо только по синусам. Таким образом, с учетом разложения вида (4)–(6) система в частных производных (2) сводится к k системам обыкновенных дифференциальных уравнений восьмого порядка в нормальной форме [2, 8]

^ Y = A k ( s ) Y k + / k ( s )    ( k = 0,1, 2, - ),

Ak ( s ) = |^)(s )||     (i, j = 1, - 8),   s 0 ^ s ^ sL ,    fk ={ fk , f2 k , -, f! k } , с граничными условиями B1Y (s0 ) = b1, B2Y (sL ) = b2. Здесь B1, B2 — заданные матрицы, b1,  b2 — заданные векторы.

Краевую задачу (7) с соответствующими граничными условиями будем решать методом дискретной ортогонализации [2, 9], основанном на ортогонализации векторов решений задач Коши в конечном числе точек изменения аргумента. Во многих случаях система (7) за счет неоднородности механических и геометрических параметров и нагрузки является жесткой и содержит амплитудные значения разрешающих функций. Ряды Фурье для функций (4)–(6) будем строить на дискретном множестве точек [10, 11].

При решении прикладных задач обычно удерживают несколько первых членов дискретного ряда Фурье, так как коэффициенты Фурье быстро убывают, и вследствие этого уменьшается влияние больших гармоник. Скорость убывания коэффициентов Фурье связана с дифференциальными свойствами функции, продолженной на весь интервал ( -от , от ). Значения коэффициентов Фурье и количество гармоник определяют точность приближений.

Если известно значение распределенных нагрузок q_s , q ₆ , q _Y по произвольно выделенной кольцевой поверхности длиной a_s (Рис. 1), то, согласно (4), для интегрирования уравнения (7) значение любой из компонент нагрузки должно быть представлено в виде разложения в ряд Фурье [10–12]:

а от qf = -4 + ^(ak cos к6 + bk sin к6).                                    (8)

² k = 1

3.    Метод решения задачи

Поскольку в работе применяется подход, предполагающий построение решения в виде рядов Фурье для функций, заданных на дискретном множестве точек, то для создания этого множества на поверхность оболочки нанесем криволинейную сетку с равным шагом по меридиану. Полученные окружности разобьем на одинаковое количество элементов, вследствие чего придем к множеству виртуальных оболочечных элементов [8]. На рисунке 1 показан виртуальный оболочечный элемент с размерами as и а9. Будем считать, что на множестве виртуальных элементов известно значение распределенных нагрузок qs, q9, qу. Таким образом, на каждом виртуальном элементе имеем известное постоянное значение компоненты нагрузки q .

Обычно в рамках теории оболочек рассматриваются нагрузки, симметричные относительно какой-либо поперечной оси [2–4]. Если за ось симметрии принять ось x (Рис. 1), то можно использовать разложение (4)–(6), в котором коэффициенты обуславливаются требованиями задачи и таковы, что позволяют обеспечить быструю сходимость ряда.

При решении задачи определения напряженного состояния оболочки вращения, находящейся под действием нагрузки, заданной в окружном направлении в виде ступенчатой (дискретной) функции, встают вопросы, связанные с суммированием рядов Фурье. Вследствие того, что при вычислении приходится усекать ряд и учитывать конечное число его членов, возникает явление Гиббса [12]. Его суть заключается в том, что при наличии разрыва заданной функции ее значения справа и слева от точки разрыва могут различаться [ 2 ] . Существуют подходы по сглаживанию колебаний Гиббса, например умножение всех членов ряда на множители Ланцоша [ 13 ] .

При действии на оболочку нагрузки, нормальной к ее поверхности — q _Y , или касательной к образующей — q_s , можно удерживать коэффициенты дискретного ряда Фурье только при косинусах [ 11 ] . В случае симметричных относительно оси x нагрузок аппроксимирующая функция нагрузки будет четной. В силу периодичности (период 2 N ) и четности этой функции ее можно разложить в ряд Фурье с коэффициентами [11]

2 Г1      N-1       пк. 1, ak=n 2qо+^q-cosNF1+2("1) qN —            i=1

bk = 0, где qi — значение компоненты нагрузки на каждом виртуальном элементе.

В работах [ 8, 14 ] для функций, характеризующих напряженное состояние конструкций, на которые нагрузка действовала по нормали к поверхности — q _Y , использовалось разложение с коэффициентами (9). Затем вычислялась разность между исходной и аппроксимирующей функциями, которая во всех случаях не превысила 0,71%.

Однако в прикладных задачах для тел вращения могут встречаться нагрузки, не симметричные относительно поперечной оси, а распределенные произвольным образом. Это могут быть ветровые нагрузки, силы инерции при землетрясениях [15], нагрузки, рассматриваемые в разделе 4 данной статьи. Такие нагрузки необходимо раскладывать в ряд по косинусам и синусам [1, 15]

от                                  от qs (s, 9) = ^ q7 (s) cos к9 +^ qsn (s) sin к9 , к=0

отот q9 (s, 9) = -^ q9im (s) sin к9 + ^ qan (s) cos к9,(10)

к=1

отот qY (s, 9) = £ q7 (s) cos к9 -У q7 (s) sin к9 . к=0

Верхним индексом sim отмечены симметричные компоненты нагрузки, а индексом ans — антисимметричные компоненты. Следовательно, для симметричных компонент вектора разрешающих функций надо добавлять в ряд слагаемые вида от

Ф ( s , 9 ) = £ ф ( s )sin к 9 ,                                    (11)

к = 1

а для антисимметричных компонент от

Т ( s , 9 ) = ^ Y ( s )cos к 9 .                                     (12)

к = 0

При такой записи выражений для нагрузок функции антисимметричной деформации определяются точно такой же системой уравнений, как и функции симметричной деформации. Поэтому при нахождении напряженно-деформированного состояния оболочек от нагрузки вида (10) вектор разрешающих функций (3) можно представить как сумму компонент Y = Y1 + Y2, где Y1 — вектор разрешающих функций при разложениях (5), (6), а Y2 — при разложениях (11), (12).

В разнообразных разложениях в ряд Фурье, приведенных в различных литературных источниках, можно выделить коэффициенты, дающие малую погрешность аппроксимации [ 16 ]

a

1 N -1

k = N S qi

2пki       ,     1 N-1    . 2пki cos ,      b. =     7 q, sin ,

N ’ ^k N ^S ‘ N ’

( k = 0, ... N /2).

Ряды Фурье с коэффициентами вида (13) используются в акустике при анализе сигналов в случае разложения их на гармоники. При этом считается, что сигнал — функция периодическая с периодом N .

Точность решения задачи (вычисленного напряженно-деформированного состояния оболочки) зависит как от точности аппроксимирующей нагрузки (8), так и от точности интегрирования системы уравнений (7). Величина погрешности может быть установлена сопоставлением с решением аналогичной задачи другим методом, численным либо аналитическим. Поскольку разложение нагрузки в дискретный ряд Фурье — это суперпозиция нагрузок, приложенных на множестве виртуальных элементов, то для обоснования предлагаемого метода в работах [ 8, 14 ] решение с коэффициентами вида (9) сопоставлялось с решением при помощи метода конечных элементов. Реализована задача для оболочки, нагруженной распределенной нагрузкой q _Y , действующей на одном виртуальном элементе. Значения различных компонент напряженно-деформированного состояния для изотропных [ 14 ] и ортотропных [ 8 ] оболочек сравнивались с аналогичными результатами, полученными в вычислительных комплексах ANSYS [17] и Cosmos [18]. Достигнуто хорошее совпадение величин компонент напряженного состояния.

4.    Численный пример с применением дискретных рядов Рис. 2. Цилиндрическая оболочка, лежащая на опоре

В качестве примера рассмотрим тонкую оболочку ( h = 0,006 м) длиной L = 2,24 м, лежащую на жестком основании. Ширина основания составляет b = 0,24 м, длина дуги контакта 2 t «стягивается» углом 128° (Рис. 2). Между основанием и оболочкой имеются 11 упругих прокладок одинаковой длины. Этот расчетный случай представляет передачу нагрузки от вагона–цистерны на лежневые опоры.

Ранее в [ 19 ] путем решения контактной задачи найдено распределение контактного давления q , действующего на эту оболочку. При расчете было принято: внешний радиус цилиндрической оболочки R = 1,50 м; радиус опоры R = 1,50 м; модуль упругости E = 2,1 ■ 10⁵ МПа; коэффициент Пуассона ц = 0,3; главный вектор вертикальной нагрузки P x = 45 ■ 10⁴ Н. Граничные условия имели вид:

N r = N z = M s = S = 0 при s = 0, N_r = N_z = M_s = S ˆ= 0    при s = L .

Для того чтобы установить напряженно-деформированное состояние оболочки описанным выше методом, аппроксимируем контактное давление q в виде (8). Окружность оболочки разобьем на элементы с угловым шагом А9 = 2 ° , который «стягивает» виртуальный элемент длиной a ₉ . Таким образом, окружность оболочки аппроксимируем 180 виртуальными элементами, дугу прокладки — четырьмя, а зазор между прокладками — двумя виртуальными элементами. По ширине области контакта в меридиональном направлении зададим один виртуальный элемент a s = b .

На рисунке 3 а показано распределение контактного давления q , найденное в [ 19 ] . Горизонтальная ось изображает область контакта, длина которой определяется углом 9 . Естественно, при вертикальной нагрузке P x контактное давление симметрично относительно плоскости 9 = 180 ° . На рисунке также изображена нагрузка q_f , представленная в виде разложения в ряд Фурье с коэффициентами (13); кривые полностью совпадают.

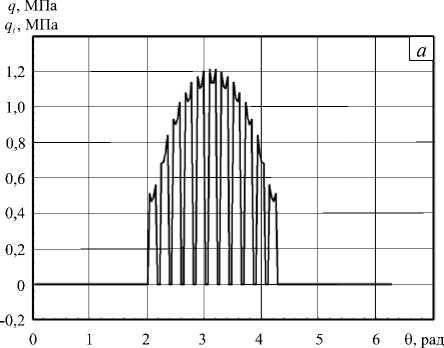
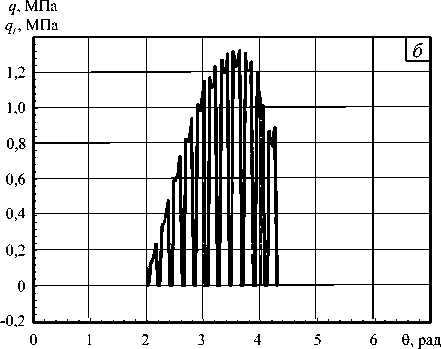
Рис. 3. Характер контактного давления при взаимодействии оболочки с основанием при вертикальном ( P_x ) ( а ) и смешанном ( P_x и P_y ) ( б ) нагружении

Относительная погрешность 8 , вычисленная как 8 = \q - qf |- q _ср ¹ - 100%, где q _ср — среднее значение нагрузки по всем точкам расчетной сетки, не превышает 0,0005%. Добавим, что путем численного эксперимента было установлено следующее: в разложении в ряд Фурье (8) с коэффициентами (13) необходимо удерживать k = N /2 гармоник. Таким образом, в данной задаче соотношение (8) содержало 90 членов ряда.

Поскольку действующая нагрузка симметрична относительно вертикальной оси, то для решения задачи можно использовать и разложение с коэффициентами (9). Такой случай исследован в работе [ 14 ] . При этом погрешность составила 8 = 0,4 %.

Рисунок 3 б содержит распределение контактного давления q при действии на оболочку вертикальной ( P x = 45 - 10⁴ Н) и поперечной ( P y = 8,848 - 10⁴ Н) нагрузок (см. Рис. 2). Данный расчетный случай описывает прохождение вагоном–цистерной криволинейного участка пути, на котором и возникает дополнительная центробежная сила P_y . Из рисунка видно, что поперечная нагрузка нарушает симметрию контактного давления относительно оси x , и следовательно, такое нагружение возможно описать только разложением с коэффициентами (13). Кривая нагрузки q_f , представленной в виде разложения в ряд Фурье, совпадает с графиком q . Относительная погрешность 8 не превышает 0,0005%.

5.    Численный пример с применением обычных и дискретных рядов Рис. 4. Цилиндрическая оболочка под действием внешней нагрузки, которая равномерно распределена на двух виртуальных элементах

Рассмотрим задачу для однослойной ортотропной цилиндрической оболочки, на которую действует нормальная внешняя нагрузка P I = 1000 Н, равномерно распределенная на одном виртуальном элементе с размерами a ₀ х a s . Данная задача решена в работе [ 8 ] для случая, когда центр виртуального элемента имеет координаты s = L] 2, 0 = 0 . На рисунке 4 показан такой случай нагружения ( q I = P I х ( a s х а ₀ ) ^{- 1}).

Модули упругости и сдвига, коэффициент Пуассона имеют следующие значения: E 1 = 4,65 - 10 4 МПа, E ₂ = 0,7 - 10⁴ МПа, G 12 = 0,7 - 10⁴ МПа, ц 1 = 0,25. Геометрические размеры и граничные условия совпадают с задачей из раздела 4. Поскольку нагрузка симметрична относительно вертикальной оси, то она может быть представлена в виде разложения по косинусам в обычный ряд Фурье с коэффициентами [ 8 ] :

a

P пRas

2 P sin ( к А0/ 2 ) a                        ,

пRask А0

b_k = 0.

Здесь А0 = 2 ° — угол, который «стягивает» виртуальный элемент по окружности. Аналитическое разложение в ряд с коэффициентами (14) описывает четную функцию в виде ступеньки, симметричную относительно 0 = 0 ° .

После интегрирования системы (7) с учетом разложения с коэффициентами (14) имеем компоненты напряжений на внешней и внутренней поверхностях оболочки ( ст ₅ — меридиональную, ст₀ — окружную, т _{5 0} — касательную) и перемещения в каждой точке срединной поверхности по трем направлениям ( ur. , u z , v ).

Рисунок 5 а демонстрирует изменение радиального перемещения u_r (кривая 1 ) по длине окружности, измеряемой углом 0 , в сечении оболочки 5 = L /2 . В решении удерживалось 200 гармоник. Перемещение u_r выбрано как наиболее информативный параметр, по которому можно оценить деформированное состояние оболочки. Видно, что в месте, где приложена нагрузка, прогиб максимален. В работе [ 8 ] полученное распределение u_r сравнивалось с решением, найденным методом конечных элементов. Поскольку внешняя нагрузка симметрична относительно вертикальной оси x , то и радиальный прогиб симметричен относительно сечения 0 = 0 ° .

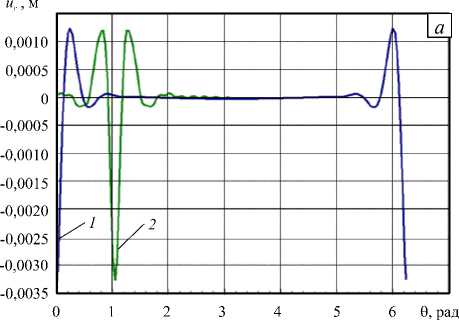
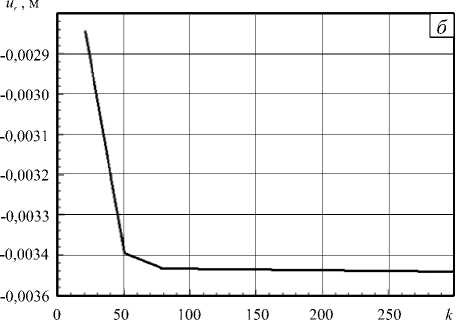
Рис. 5. Изменение радиального перемещения u r по длине окружности для сечения 5 = L /2 ( а ) и в точке поверхности

оболочки с координатами 5 = L /2 , 0 = 0 ° в зависимости от количества суммируемых гармоник к ( б )

Как отмечено выше, при суммировании гармоник, описываемых обычными рядами Фурье, часто возникает вопрос о количестве удерживаемых членов ряда в соотношении (8). Рисунок 5б содержит изменение радиального перемещения ur в точке с координатами 5 = L/2, 0 = 0° в зависимости от количества суммируемых гармоник k . Видно, что в данной задаче необходимо удерживать не менее 100 членов ряда, поскольку далее решение приближается к асимптоте, и количество гармоник в решении не влияет на результат.

Представим в рассматриваемой задаче внешнюю нагрузку в виде дискретного ряда с коэффициентами (13). Сначала рассмотрим расчетный случай для внешней нагрузки P, = 1000 Н,

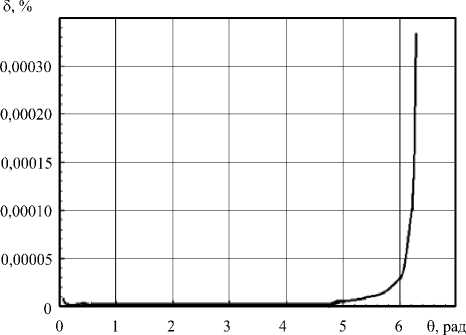
Рис. 6. Изменение по окружности оболочки относительной погрешности 3 при аппроксимации приложенной ступенчатой нагрузки дискретным рядом Фурье

равномерно распределенной на виртуальном элементе, центр которого имеет координаты 5 = L /2, 0 = 0 ° . В соотношении (8) удержим 90 членов ряда.

На рисунке 6 показано изменение относительной погрешности 5 в зависимости от угла 0 при аппроксимации ступенчатой нагрузки дискретным рядом. Погрешность, вычисленная как 5 = qq - q^ | • q _ср ^{- 1} • 100%, не превышает 0,0003%. Увеличение 5 в конце интервала представления функции, по-видимому, можно объяснить накоплением погрешности за счет недостаточно точного задания числа п , через которое определяется шаг.

Далее рассмотрим расчетный случай для элемента с координатами центра 5 = L /2,

6 = я/3. Согласно рисунку 4 на элемент действует нагрузка Р„ = 1000 Н. Такую нагрузку можно аппроксимировать только дискретным рядом с коэффициентами вида (13). На рисунке 5 а кривая 2 показывает изменение радиального перемещения u r в сечении 5 = L /2 именно для этого вида нагружения. В месте, где приложена нагрузка, наблюдается максимальный прогиб. Из рисунка 5 а видно, что кривая 2 сдвинута относительно кривой 1 на угол я/3 .

6.    Заключение

Из проведенных расчетов следует, что при удержании необходимого количества суммируемых гармоник аппроксимирующая функция q_f достаточно точно представляет различные внешние поверхностные нагрузки. Предложенное разложение в дискретный ряд Фурье по косинусам и синусам с коэффициентами (13) имеет незначительную погрешность аппроксимации и более универсально, чем разложение с коэффициентами (9), так как способно описывать произвольные несимметричные нагрузки. При этом в разложении в ряд Фурье (8) с коэффициентами (13) необходимо удерживать k = N /2 гармоник. Предложенное разложение с коэффициентами (13), по-видимому, целесообразно применять при аппроксимации внешних нагрузок для тел вращения, исследуемых с помощью и других сеточных методов, например метода конечных элементов.

Важно, что использованное в работе разложение нагрузки в дискретный ряд Фурье позволяет понизить размерность задачи при обеспечении высокой точности аппроксимации произвольной внешней нагрузки.

Работа выполнена в рамках Программы фундаментальных научных исследований УрО РАН (проект № 15-10-1-22).