Определение неизвестных коэффициентов математической модели

Актуальность темы: Применение современных биотехнологических методов при переработке каолинов, занимающих важное место в экономике нашей страны, считается экологически чистым и экономически эффективным методом. На сегодняшний день при изготовлении фарфоровых изделий, скульптуры используется качественный импортный каолин. Это приводит к повышению себестоимости продукта и становится причиной увеличения финансовых затрат. Качество каолина местного Ангренского месторождения низко и содержит элемент железо, который препятствует его использованию. При очищении элемента железа, снижающее качество каолина наряду с химическими методами, развитых странах используются современные биотехнологические методы железоокисляющих бактерий. В этом направлении в нашей стране ведутся научные исследования по внедрению биотехнологических методов очистки. При этом задача параметрической идентификации состоит в экспериментальном определении характеристик объекта. Оценивание параметров объекта производится в рамках математической модели определенного класса. При этом различие между данными, полученными на реальном объекте и на соответствующей математической модели, должно быть по возможности минимальным. Подробное обсуждение методов параметрической идентификации, в том числе их выход и анализ условий сходимости, можно найти в работе [7], а также в [10,11].Чтобы избежать ситуации, когда малые ошибки экспериментальных данных могут повлечь большие ошибки в определении констант, требуется оценка корректности постановки задачи идентификации. Кроме того, важен вопрос о достаточности экспериментальных данных, возникающий при исследовании конкурирующих моделей. Эти существенные аспекты рассмотрены в работах [12,13].Скорост бактериального окисления закисного железа была увелечена путем аэрирования растворов и добавления солей фосфора. При дополнительной аэрации сжатым воздухом (2,8-3,0 м\мин) и добавленин бактериальных затравок из чанов при температуре 25-35 С в условиях стационарного культивирования и при избытке кислорода, двуокиси углерода и других компонентов. Скорость окисления в культиваторе достигает 50 г\скорость окисления определяется скоростью роста бактерий, которая в свою очередь зависит от способа и условий их культивирования. Время генерации бактерий на сред с при температуре 25-35С колеблется от 3,6 до 10г.Таким образом, процессе биотехнологического обезжелезиения каолина необходимо учитывать количество железа, которое содержится в сырье, а соотношение Т:Ж и рН поддерживать таким, чтобы не было повторного осаждения железа уже в виде гидроксиде или создать условия, при которых 3-ч валентное железо будет оставаться в растворе. Однако увеличение концентрации клеток в маточном материале в 10 раз способствует сокращение времени обогащения не на 70-80 часов, а толка 25-30 часов. Многочисленными условиями, показано что скорость окисления прямо пропорцианально концентрации фемента.

Влияние количества вносимого в суспензию каолина маточного материала бактерии Thiobacillus ferrox титр културы.

Объем маточного материала, вности, в расчете на 1л суспензии, мл.	Титр културы суспензии, кл\мл.	Количество железа, вносимого в суспензии с маточными г\л	ПРИМЕЧАНИЕ
20	2*10	0,016	Титр клеток в суспензии ниже
25	2,5*10	0,02	оптимального Титр културы
30	3*10	0,024	достаточен для
35	3,5*10	0,028	развития процесса обогащения.
40	4*10	0,032	Количество вносимого железа превышает

оптимальные нормы.

Количествр сьемов по 1\2 объема жидкой фазы реакционной смеси при максимально достимимой концентрации железа в растворе в зависимости от соотношения Т:Ж

Соотношение Т:Ж	Соотношение масса; объем г:мл	Удавляемый объем жид фазы, мл	Удавляемая масса железа, всего, гр	Удавляемая 1-кратно масса железа, г	Число съемов жидкой фазы, раз.
1:1	500:500	250	2,5	0,2	12
1:2	333:666	333	1,66	0,264	6
1:5	250:750	375	1,25	0,3	4
1:4	200:800	400	1,0	0,32	3
1:5	166:830	415	0,83	0,332	2,6

Fe O 3      f           Fe (SO 4 ) 3 + H 2 O→Fe(OH) 2 SO 4

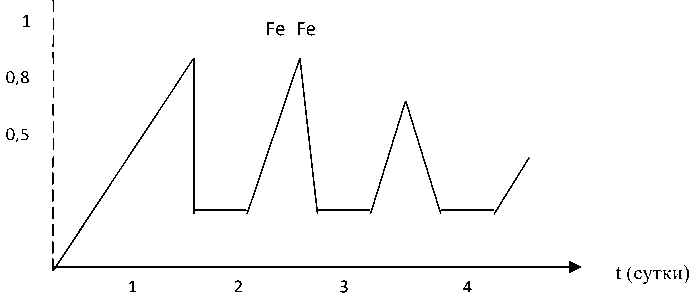
Съемно-доливной способ ведения процесса биотехнологического обогащения каолина.

А-кривая выхода железа в жидкую фазу; а,б,в- моменты остановки барботирования;

Г-время остановки-окончания процесса; П- паузы на осаждение каолина, слив 1\2 части жидкости фазы и внесение равного объема питательной среды.

В процессе барботирования реакционной смеси начиная с 2-ч суток производим отбор части суспензии и анализ на содержание оксида железа. По достижении концентрации в суспензии 0,75г\л барботирование останавливает на 3-4 часа, затем откачиваем или сливаем верхнюю над осадочную часть, стараясь не взмучивать осадок сливание части жидкой фазы производим периодически до тех пор, пока концентрация оксида железа в ней перестанет возрастать и остановится на пороге менышей 0,75 г\л

Результаты исследований: Для повышения качества каолинов предложена схема, включающая в себя основные стадии дезинтеграция, отделение крупных каменистых и включений, электромагнитная сепарация, сгущение суспензии каолина, сушка. Такая схема позволила увеличить содержание алюминия (более 35%), снизить содержание железа до 0,9% и оксида титана до 0,7%.

В процессе обогащения каолина на детерминированные кинетические зависимости накладывается множество возмущений, носящих характер, чем и объясняется возникающая необходимость периодической или постоянной подстройки коэффициентов модели. Задача оценивания констант связана с надежным выборам метода, обеспечивающего требуемую точность и быструю сходимость поиска. В настоящее время разработано достаточно большое количество методов оценки кинетических констант [6]. Среди них наибольшее распространение получили метод наименыших квадратов, метод максимального правдоподобия и метод оценок на основе теоремы Байеса.

Однако следует заметить, что при оценке кинетических констант биохимических и микробиологических реакций до сих пор нередко используется графический метод, уступающий по точности аналитическим и трудно поддающийся формализации на ЭВМ [9].

Как показал опыт, данный метод сопряжен с определенными трудностями, особенно для специалистов, не обладающих достаточным опытом экспериментального исследования технологических процессов. Только после многочисленных экспериментов и контрольных расчетов можно убедиться в правильности полученных значений коэффициентов. Поэтому нами с целью преодоления этих трудностей, ускорения расчетов и получения более точных и достоверных результатов использованы методы приближенного дифференцирования. Биотехнологический процесс описывается в общем вида уравнением

Г = f(c) + К (5)

Значения f(C), как правило на первоначальном этапе представляют собой результат экспериментов. Полученные экспериментальные данные наносятся на график, где осью абцисс служит С, а осью ординат- t. В качестве С могут выступать концентрация субстрата – S и бактерия – Х.

Поскольку концентрация субстрата меняется в широких пределах и имеет прямую связь с другими биокаталическими процессами и явлениями, удобнее и точнее определять значения интересующих нас коэффициентов именно через данный параметр. Концентрацию субстрата-S также точнее и быстрее можно определить экспериментальными приемами.

Какой бы прцесс не описывался рассматриваемой нами функцией Y = f(C) + К производную Y ' с физической точки зрения интерпретировать как скорость, с которой протекает этот прцесс [10,13]я нахдения на отрезке ^[ t o t ^] производных S'(I) приближенно заменим функцию интерполяционным полиномом Лагранжа, построенным для требуемых точек

Тогда S'(t) для двух точек приобретает следующий вид:

_       1г       2g —1 „  1

S1(t)=-[vSo +  2  V24

Где g = tt-^ tl представляет собой число шагов, необходимых для достижения точки t, исходя из точки t0 и h = tl=1 — ti(t = 0,1,2, ...,п)

здесь - VSi определяются методом конечных разностей. В итоге получаем два алгебраических уравнения с двумя неизвестными в следующем виде:

Г-S1(to) = [a,^) + mi]%o

I S¹(t i ) = [a₂, g(tj + m₂]x i

Здесь значения S ' (t₀),S ' (t i ), известны: они определяются по результатам экспериментов; - неизвестные коэффициенты.

Для решения системы уравнений применяем метод последовательного исключения неизвестных (метод Гаусса). В результате получим:

a1 = 1,57 m1 = 0,068 a2 = 1,36 m2 = 0,059

t- время	SiO2	TiO2	AL2O 3	Fe2O3	K2O
6	53,51	0,63	27,80	2,77	1,68
12	51,58	0,64	33,04	1,58	1,60
18	50,18	0,66	34,13	0,98	1,64
24	49,78	0,68	34,80	0,80	1,62

Рис. 1.

Окисленые железа

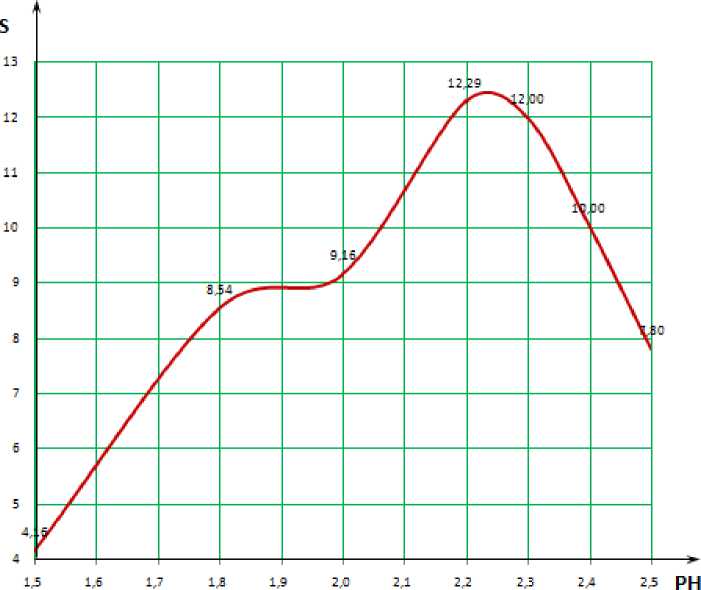
Рис. 2.

t^ (6 12 18 24 30)Т

SiO2:= (53.51 51.78 50.18 49.78 48.90)Т

А12ОЗ := (27.80 32.04 34.13 34.80 35.10)Т

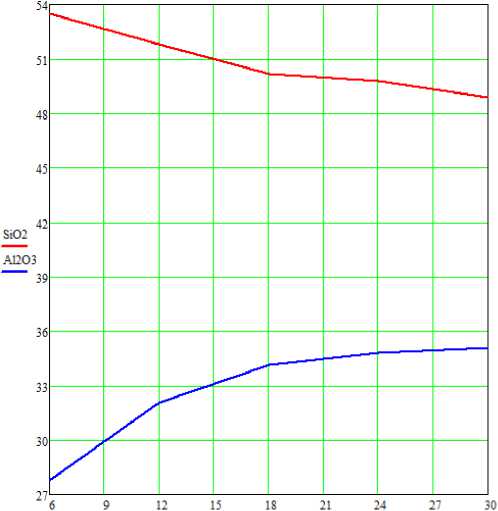
А1₂О₃-Алюминий SiO₂-KpeM назем

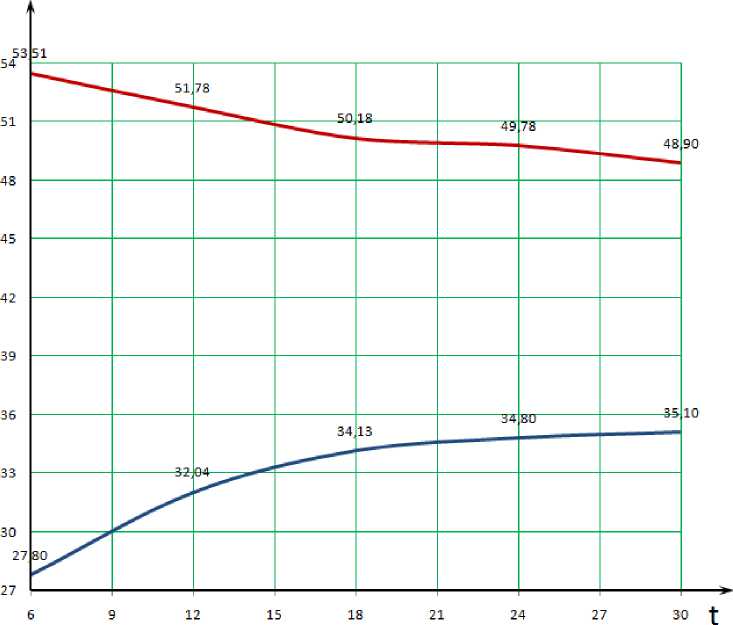
Рис. 3.

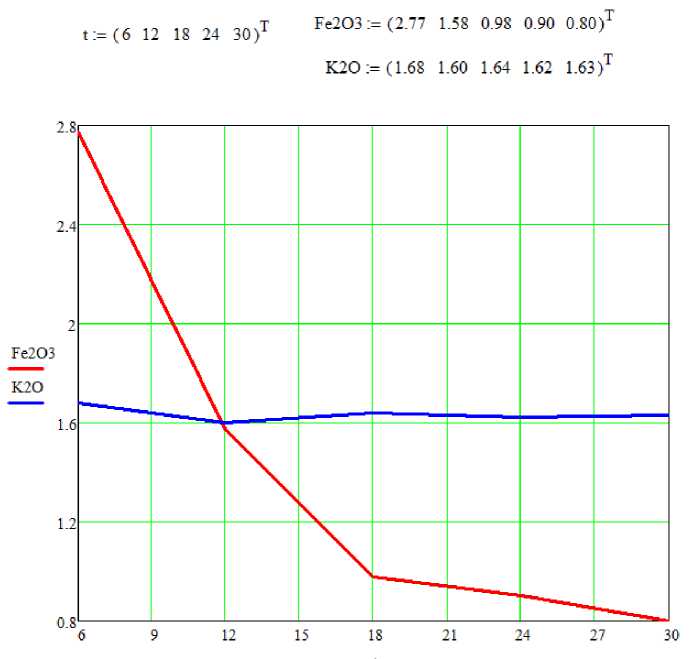
K70 - Калий Fe?O= - Железа

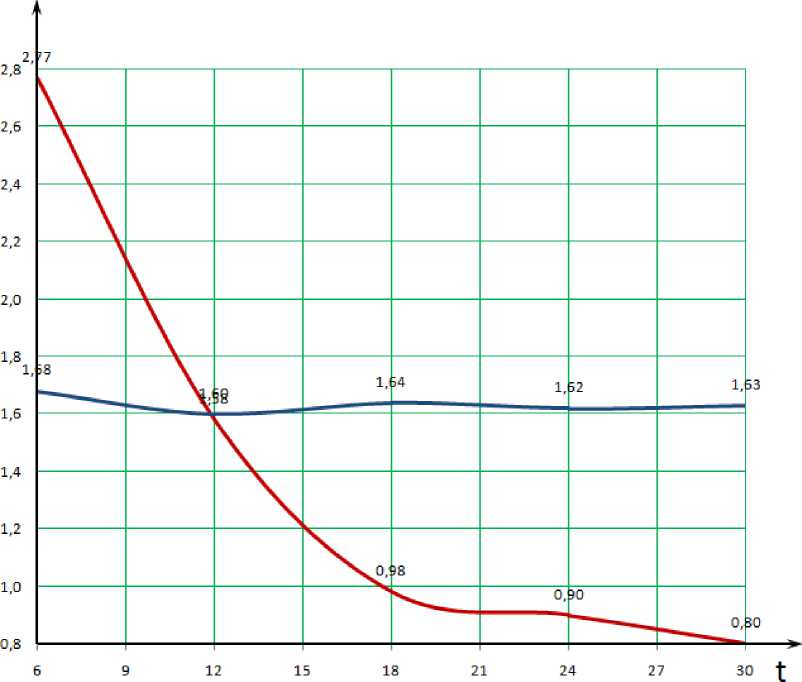
Рис. 4.

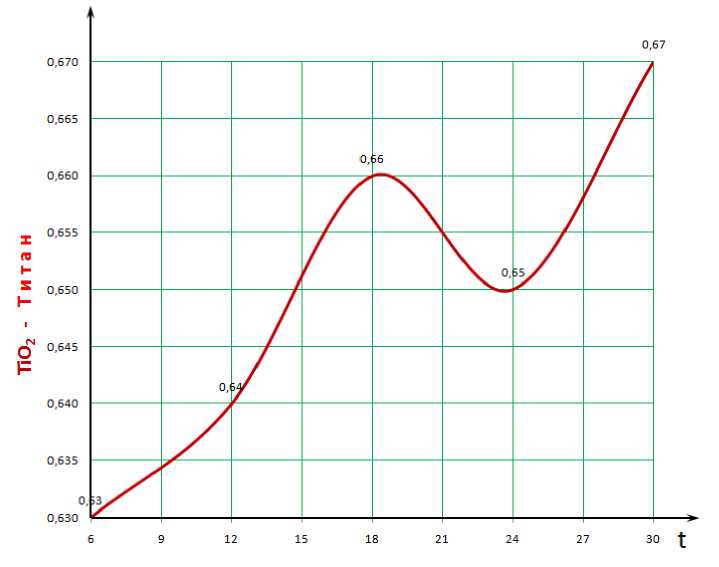
Рис. 5.