Определение оптимального числа дополнительных слоёв передаваемых данных схемы сокрытия сетевой латентности

Одним из ключевых компонентов эффективности массивно-параллельных вычислений является организация обмена данными между вычислительными узлами. При передаче данных существенные временные задержки могут приходиться на сетевую латентность. Таким образом возникает необходимость в использовании алгоритмов перекрытия задержек передачи данных для повышения эффективности параллельных Для цитирования

вычислений. На данный момент практика применения программных методов перекрытия задержек обмена данными показала существенное повышение масштабируемости и производительности параллельных приложений [1, 2]. Большое количество работ посвящено аппаратным реализациям методов перекрытия задержек обмена данными [3-9]. Стоит отметить, что разработка программных методик является предпочтительным направлением, так как позволяет, с одной стороны, не закупать

дополнительное оборудование, а с другой, может применяться совместно с аппаратными методиками. В отечественных и зарубежных работах не рассматривается способ выбора числа слоёв дополнительно передаваемых данных R. Наша гипотеза состоит в том, что оптимальное число дополнительно передаваемых данных может быть выражено через параметры среды передачи данных и параметров параллельного приложения.

• 1.1    Модель сети

Для оценки времени передачи данных нами использовалась модель, предложенная Хокни:

И должно выполняться соотношение: Np

N ячеек

П \ V\⁽ⁱ⁾ d          ячеек

d e { x , y , z }

i = 0

m

Чд = ^Тл + —

B

где т пд - время передачи m бит данных с пропускной способностью сети B [бит/секунда].

• 1.2    Оценка размера сетки на процессе

В данной работе рассматривается простейший случай декомпозиции структурированной сетки по процессам:

NT =

N d - + 1

N d^p

N d

I N d

P <  N d % N d

, d e { x , y , z } PT >  N d % N d

• 1.3    Оценка времени счёта

В отсутствие наложения счёта и передачи данных, время счёта можно представить суммой времени обмена данными и непосредственно вычислений.

т = N _tt ( T c ( N Я ‘L ) + 2 т пд ( N Я ) )) (2)

Где количество граничных ячеек на i -ом процессе для двумерного случая без использования стратегии B+2R выражается как:

N ⁽ⁱ⁾ = 4 N и N и гя x y

Очевидно, что время счёта т _С является функцией от числа ячеек, подвергающихся счёту на i -ом процессе N⁽^ ) , а время передачи данных - функцией от количества ячеек и объема памяти, занимаемой ими.

Рассмотрим случай использования стратегии B+2R. Под R будем понимать количество слоёв ячеек соседних процессов.

т =

N                 R ⁴

2 N n T „ _d ( N _r ( R ) ) + Ут_с ( N Я^

R                         r = 1

r = 1

+ N r ( r ) ) (3)

где N dd¹ ) - количество ячеек по измерению d на i -ом процессе,. Nd - количество ячеек по заданному измерению в базовой сетке, Pd¹ ) -номер i -го процесса по заданному измерению в сетке процессов. Таким образом, количество ячеек на одном процессе выражается как:

N(i)

ячеек

П N ()

d е { x , y , z }

где N_n - максимальное число соседей в сетке процессов. Для двумерного случая с использованием стратегии B+2R N_n = 8 , для трёхмерного - N_n = 26 , при условии, что R <  N_d . Функция, определяющая количество ячеек передаваемых как R слоёв ячеек от соседа, будет определена как показано в уравнении 4 для двумерного случая.

N R = 2 N _x i ) R + 2 N yi ) R + 4 R ² = 2 R [ N Xi ) + 2 R + N yi ) ]

N т =    2 N т

R n 1

+ т N c ячеек

2 R (2 R - 1)( R - 1) R +--

A   4 N^sN Bae R ( N + N + 2 R )

+ R ( R - 1)( N x + N y ) | + —--- ^y----L

V             B

8т

8 R

8 i       (N.

⁸ N. т I R ³ +1 - it -24 N s N Base

3 it С I           О D         С C

V V 3 в

+ 3 N_ltB y ( N + N - 2) R ² - 2 NN т cx y           n n

Взяв производную уравнения 5, мы получаем выражение 6, приравняв которое 0, получаем кубическое уравнение, решением которого является оптимальное для данного вычислительного комплекса и данной задачи R. Стоит отметить, что решение необходимо выбирать, следуя нескольким ограничениям. С одной стороны, R должно быть положительным вещественным числом. При определённых конфигурациях МВК может оказаться, что уравнение 6 не имеет решений в области вещественных чисел, это соответствует случаю, когда небольшая латентность сети позволяет пересылать данные существенно быстрее, чем считается ячейка.

_T = N iL

R

N_R = 2 R 4 r R ² + NN + N_XN_Z + NN + 2 R ( N + N + N_z ))

xy xz yz   xyz

2 N j n + T c I 2 R ² ( R - 1 ) 2 + N c R + 3 R ( 2 R - 1 )( R - 1 ) ( N + N + N z ) +

R (R -1)( NN + NN + NN)) + xy xz yz

⁴ N' Ba vR 4R R ² + NN + NN + NN + 2 R(N + N + N J cc    xy xz yz   xyz

— = ( 6 N t ) R ⁹ +1 NiL (- 24 Bt + 96 NB"^eN s + 8 Bt (n. + N + N Ш R ⁸ +

d^ R          it c           3 в            c         c c         c x y z

N± (6 Bt + 24 N B^ N^N, + N_v + N_z ) - 6 Bt ( N + N_v + N_z ) + 3 Bt N^^ + + N_XN_Z + NN )) | R ⁷ + 3 B c  ccxyz  cxyz  cxyxzyz

( - 2 N t N _n T „ ) R ⁵

В выражении 8 представлена зависимость времени счёта от числа слоёв передаваемых соседями данных. Приравнивая производную выражения 8 нулю, мы находим минимум искомой функции (рисунок 1) . Данное выражение не учитывает времени, которое затрачивается на подготовку данных к пересылке, и обработки данных во время приёма. Тем не менее, выражение хорошо согласуется с результатами экспериментов. Для эксперимента использовалась конфигурация из 20 машин. Решатель содержал уравнение переноса для

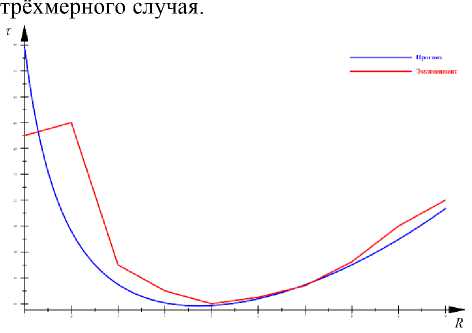
Рисунок 1. Зависимость времени счёта от R

Figure 1. Dependence of calculation time on R

График производной зависимости времени счёта от числа слоёв передаваемых данных (рисунок 2) показывает пересечение близко к 5