Определение оптимальных параметров моделирования для максимально точных расчётов энергий в ОЦК-железе

Сплавы на основе железа, несмотря на развитие производства других металлов, пластмасс, керамики, композитов, остаются основными конструкционными материалами. Первопринципное моделирование ОЦК-железа проводилось неоднократно, существует множество работ по этой теме [1–9]. В работах [1–4] моделирование проводилось псевдопотенциальным методом, который точно описывает электронный спектр только валентных электронов. Этого вполне достаточно для описания чистых веществ, однако может приводить к погрешностям при расчете растворов внедрения, где может возникнуть необходимость в учете более глубоких электронных уровней. Отсутствие учёта этих уровней приводит к менее точным результатам. В отличие от псевдопо-тенциального метода в полнопотенциальном происходит учёт всех электронов, что делает его наиболее точным. Данный метод используется в программном пакете WIEN2k [5–9]. В большинстве работ [7–9] отсутствует объяснение причины выбора тех или иных значений параметров моделирования. Задача выбора оптимальных параметров системы для моделирования электронных и магнитных свойств является чрезвычайно важной, поскольку от них зависит точность полученных результатов. Частично это связано с тем, что ряд параметров моделирования оптимизированы самими разработчиками пакета WIEN2k, либо группами, которые тесно с ними сотрудничают. Для расчетов сплавов на основе железа обычно используют обобщенное градиентное приближение PBE-GGA и типовые значения параметров, характеризующие базис плоских волн, которые составляющие E cut = –7 Рб, G max = 20 Рб^0,5 [10–12]. Другие параметры моделирования были оптимизированы в работах нашей группы [5–6] и составили: N_k = 3x3x3 точки; K_max = 5 а.е.^–1; R mt (Fe) = 2,0 а.е.

В версии WIEN2k_11.1 [13] произошла смена схемы расчёта полной энергии системы. Смена расчётной схемы позволила получить более быструю и монотонную сходимость. Можно предполагать, что такое изменение приведет к тому, что параметры моделирования, оптимизированные для предыдущих версий программы, должны быть переопределены. Повышение достоверности и точности прогнозирования структуры и свойств, как чистого железа, так и сплавов на его основе является насущной задачей, стоящей перед материаловедами. В связи с этим настоящая работа посвящена выбору оптимальных параметров для построения модели ОЦК-железа в новой версии программного пакета WIEN2k, обеспечивающих точность расчета полной энергии моделируемой системы не хуже 0,01 эВ.

Методика расчётов

В данной работе расчёты проводились из первых принципов методом LAPW [10] в программном пакете WIEN2k [11], обеспечивающим высокую точность расчета полной энергии при минимальном количестве подгоночных параметров. Это наиболее точный метод, используемый в рамках теории функционала плотности. Для расчётов использовался вычислительный комплекс

Физика

ЮУрГУ-Торнадо [14]. Для интегрирования в обратном пространстве и вычисления электронной плотности использовалась схема Монхорста–Пака с сеткой из N_k точек в зоне Бриллюэна. Чем больше используется точек, тем выше точность интегрирования, однако при этом возрастает расчетное время, поэтому оптимальное значение определяется из условия достижения требуемой точности энергии системы [15]. Критерием сходимости во всех расчётах было достижение точности расчета полной энергии системы, заряда и силы взаимодействия между двумя атомами не менее 10^–4 Рб, 10^–3 е и 1 мРб/а.е. соответственно. В данной работе ОЦК-железо моделировалось в суперячейке состоящей из 54 атомов железа.

Для определения энергии растворения углерода относительно фазы графита использовалась формула:

∆ H = E (Fe 54 C) - E (Fe 54 ) - E (C), (1) где E (Fe 54 C) – энергия суперячейки, состоящей из 54 атомов железа и одного атома углерода, находящегося в октапоре, E (Fe 54 ) – энергия суперячейки, состоящей из 54 ат. железа, а E (C) – энергия одного атома углерода в решётке графита. Параметры структуры графита были взяты из работы Джианг [3] ( a = 2,462 Å, c = 6,656 Å, α = 90°, β = 90°, γ = 120°).

Результаты

В данной работе проведены вычисления, с помощью которых определены оптимальные параметры, позволяющие обеспечить высокую точность расчетов с приемлемыми затратами компьютерных ресурсов. Часть параметров можно взять из нашей работы [16]. В ней моделировалось растворение углерода в ГЦК-железо на 11.1 версии WIEN2k. Эти параметры R mt (Fe) = 2,0 а.е. и R mt (C) = 1,2 а.е. Значение R mt (Fe) = 2,0 а.е. совпало со значением полученным в работах нашей группы на предыдущих версиях WIEN2k [5–6].

В первую очередь была выполнена оптимизация количества k -точек, так как этот параметр не зависит от других. Были взяты значения, задаваемые для ОЦК-железа по умолчанию: a = 2,84 Å, K max = 5,0 а.е.^–1 [5–6]. На рис. 1 представлен график зависимости энергии системы от количества N_k точек в зоне Бриллюэна.

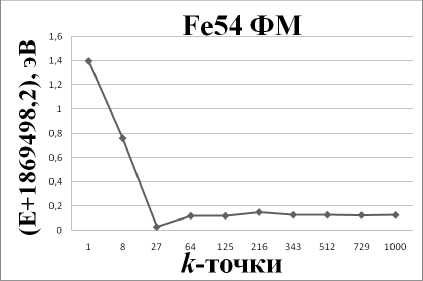
Рис. 1. График зависимости энергии системы от количества k -точек в зоне Бриллюэна

Из рис. 1 видно, что при увеличении количества k -точек выше 64 энергия системы перестаёт меняться. Таким образом, оптимальное число k -точек, необходимое для получения требуемой точности расчета полной энергии для суперячейки из 54 атомов, равно 64. Несимметричные k -сетки решено не рассматривать, ввиду того что система у нас симметричная и у неё нет никаких выделенных направлений для растяжения.

Весьма важным параметром моделирования является величина K _max. Для оптимизации данного параметра была изучена сходимость результатов расчета полной энергии системы от K max , для ферромагнитной (ФМ) фазы ОЦК-железа, представленная на рис. 2. Видно, что в новой версии пакета, в отличии от прежней, не наблюдается сходимость значений энергии при значении параметра K max = 5 а.е.^–1.

Расчеты показали, что с увеличением K max энергия системы монотонно падает, в силу чего не удается достичь такого значения параметра, после которого наблюдается сходимость в пределах 0,01 эВ для полной энергии системы. Отметим, однако, что реальной величиной, которую мы хотим получить при проведении расчетов, является не сама энергия, а ее разность для двух раз-

Ридный Я.М., Мирзоев А.А.,              Определение оптимальных параметров моделирования

Мирзаев Д.А.                         для максимально точных расчётов энергий в ОЦК-железе личных конфигураций суперячейки. В работе [6], например, проводилась оптимизация Kmax для достижения заданной точности расчета энергии растворения водорода в ОЦК-железе и было рекомендовано значение Kmax = 5 а.е.–1. Следуя примеру работы [6], мы решили определить оптимальное значение данного параметра по сходимости расчетной величины энергии растворения атома углерода в железе. С этой целью нами были определены равновесные значения параметров решётки для чистого железа и железа с одним атомом углерода (рис. 3).

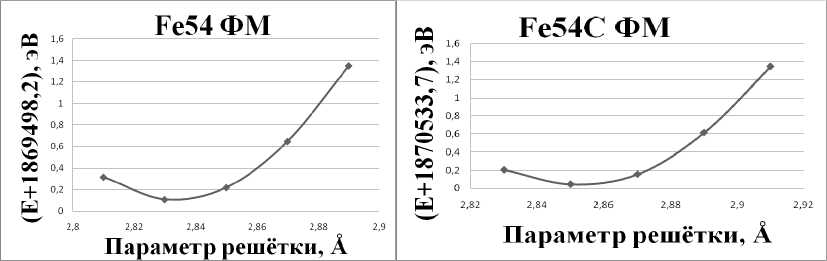
Рис. 3. График зависимости энергии системы от параметра решётки для чистого железа и железа с одним атомом углерода

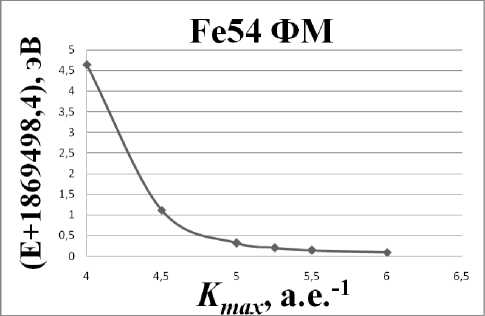
Рис. 2. График зависимости энергии системы от параметра K max

Из рис. 3 видно, что оптимальные параметры решётки a = 2,835 Å для чистого железа и a = 2,85 Å для системы с одним растворённым атомом углерода. Параметр решётки чистого железа практически совпадает с параметром определённым в работе [5], a = 2,84 Å. Небольшие отличия в 0,2 % являются следствием изменений схемы расчёта.

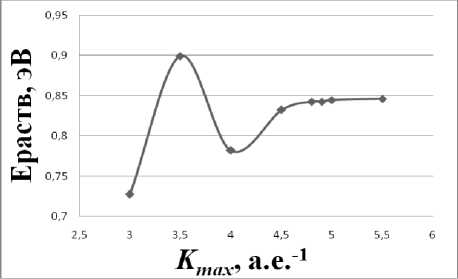
Рис. 4. График зависимости энергии растворения углерода от параметра K max

После определения равновесных параметров решётки, которые мало чувствительны к выбору параметра K max , была изучена сходимость значений по энергии растворения углерода в ОЦК -железе при вариации этого параметра (рис. 4). На графике видно, что наименьшим (оптимальным) значением параметра, обеспечивающим точность значений энергии не хуже 0,01 эВ, является K max = 5 а.е.^–1. Таким образом, определенные нами оптимальные параметры моделирования

Физика

совпадают с параметрами, полученными в работах [5–6], за исключением числа k -точек, число которых необходимо увеличить с 27 до 64 точек.

После определения оптимальных параметров моделирования проведено сравнение энергии растворения углерода в ОЦК-железе, полученной в нашей работе, со значениями, полученными другими авторами (см. таблицу ) .

Энергия растворения углерода в ОЦК-железе

Работа	Метод	Энергия растворения, эВ
[3,4]	Псевдопот.	0,7–0,74
[17]	Терм. анализ	0,99
[18]	Эксп. ( Т = 1000 К)	1,01
[19]	Эксп. ( Т = 955–1000 К)	1,14–1,19
[20]	Эксп. ( Т = 773–993К)	0,6–0,78
[21]	Эксп. ( Т = 873–1073 К)	0,63–0,98
Данная работа	Полнопот. (27 k -точки)	0,92±0,01
Данная работа	Полнопот. (64 k -точки)	0,85±0,01

Из таблицы видно, что данные по энергии растворения очень сильно различаются. Вычисленное нами значение энергии растворения углерода в ОЦК-железе лежит в середине интервала энергий растворения вычисленных экспериментально, что свидетельствует о более высокой точности проведенного моделирования, чем в работах [3, 4]. Показано, что использование параметров моделирования полученных в предыдущих версиях WIEN2k приводит к ошибке в определении энергии растворения углерода в ОЦК-железе в 0,07 эВ.

Заключение

Определены оптимальные значения основных параметров моделирования примесей углерода в ОЦК-железе, позволяющие рассчитывать энергетические характеристики системы с точностью не менее 0,01 эВ в новой версии (11.1) программного пакета WIEN2k. Показано, что:

• 1.    Для обеспечения данной точности необходимо увеличить количество k -точек до 64 по сравнению со значением k = 27, рекомендованным в работах [5, 6]. Оптимальное значение параметра K_max не изменилось и по-прежнему составляет 5 а.е.^–1.

• 2.    С использованием найденных значений параметров моделирования проведено вычисление энергии растворения атома углерода в ферромагнитной фазе ОЦК-железа, которая составила 0,85 эВ, что находится в хорошем согласии с результатами эксперимента и других первоприн-ципных расчетов. Использование параметров моделирования, полученных для предыдущих версий WIEN2k, приводит к ошибке в определении энергии растворения углерода в ОЦК-железе в 0,07 эВ.

Исследование выполнено за счет гранта Российского научного фонда № 16-19-10252 и гранта РФФИ № 16-03-00486 А.