Определение оптимальных режимов работы приспособления со шнековой подачей стеблей для уборки подсолнечника

МАМИ

ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНЫХ РЕЖИМОВ РАБОТЫ ПРИСПОСОБЛЕНИЯ СО ШНЕКОВОЙ ПОДАЧЕЙ СТЕБЛЕЙ ДЛЯ УБОРКИ ПОДСОЛНЕЧНИКА

633.854.78:631.171

В статье [1] описаны преимущества уборки подсолнечника комбайном, снабженным стеблеподающим шнековым устройством, расположенным под углом к плоскости поля по ходу комбайна. Вместе с тем, применение указанного устройства требует правильного подбора таких параметров, как скорость комбайна, скорость вращения вала шнека, а также размер шага шнека. Только в этом случае можно добиться той эффективности процесса уборки подсолнечника, о которой упоминалось в статье [1]. Проблема здесь в том, что при проходе через шнек стебель подсолнечника подвергается динамическому воздействию периодического характера вследствие биений со стороны вращающегося вала шнека. При оптимальном подборе соответствующих характеристик движения, отмеченные динамические эффекты должны быть минимальными и не приводящими к перегрузкам, при которых возможено осыпание семян из корзинок подсолнечника. Решению отмеченных вопросов и посвящена предлагаемая статья.

Исследование выполнялось на примере конкретного образца уборочного комбайна, снабженного шнековым подавателем. В данной статье обсуждению подвергаются лишь те конструктивные и кинематические характеристики, которые связаны с динамикой прохождения стебля подсолнечника через шнек.

Отметим, что в литературе по теории колебаний и динамике машин [2-7] накоплен обширный опыт по постановке и решению динамических задач для различного типа механических систем. Взяв за основу этот опыт, рассмотрим вопрос о формулировке соответствующей динамической модели применительно к случаю транспортировки вертикально расположенного стебля подсолнечника шнековым подавателем, ось которого находится под углом к горизонту (в направлении движения комбайна).

Отдельный образец подсолнечника представляет собой упругий объект, масса которого сосредоточена главным образом в корзинке с семенами. В зоне контакта с валом шнека стебель подсолнечника (вследствие естественных биений вала) испытывает поперечные отклонения периодического характера типа

A sin О t , где d[ e ¹ ] — угловая частота вращения вала шнека, a = 0,003 м — амплитуда биений. Связь между круговой частотой q [ об / мин ] вращения вала и указанной угловой частотой имеет вид

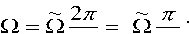
60     30

Если предполагать, что исследуемый динамический процесс происходит в диапазоне достаточно низких частот (затрагивая лишь нижнюю частоту поперечных колебаний образца подсолнечника), то в качестве модели подсолнечника можно использовать схему невесомой упругой консольной балки с сосредоточенной массой (масса корзинки) на свободном конце. Определив каким-либо образом жесткость

c

Н м

такой балки в условиях действия попе- речной силы F , приложенной к ее свободному концу, придем к динамической модели растения подсолнечника типа “масса на пружине” (см. рис. 1).

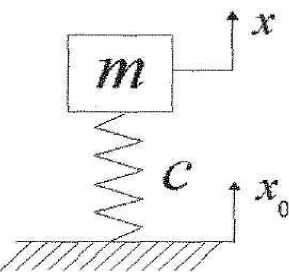
Рисунок 1 – Расчетная динамическая модель типа "масса на пружине"

Здесь x и x – поперечные перемещения корзинки подсолнечника и точки контактного взаимодействия стебля с валом шнека, при этом, как указывалось выше, x A sin    t .            (2)

Уравнение движения массы m (см. рис. 1) под действием силы упругости Ғ = c ( x — x₀ ) со стороны пружины, основание которой перемещается по закону (2), имеет вид:

m ax = fF , или      m x = —с(x — x0 ), или     x + xx = A sin dt.       (3)

Здесь x = a - ускорение корзинки подсолнечника, представляющее собой вторую производную перемещения x по времени, а 8 - параметр, определяемый формулой

Численное решение системы (7) с начальными условиями (8) строим с использованием схемы Эйлера [8]. Такая схема предполагает пошаговый процесс вычислений, при котором на n -ом шаге по времени производные в (7) приближенно (с учетом малости шага A t ) выражаются через конечные приращения соответствующих функций. В результате на основе (7)-(8) получаем схему вычислений:

У 1, n ₊1 = У 1, n+^ t У 2, n ,

У2,n +1 = У2,n + At8(tn )( A sin Qtn - У1,n ), tn+1 = tn + At,                                    (9)

(n = 0,1,2,...), t0 = 0, У1,0 = 0, У2,0 = 0,

c

8 = - m

которая позволяет по известным значениям

Как известно [3], величина

c

^ = Л ~

m

представляет собой частоту собственных колебаний системы типа “масса на пружине”, поэтому связь (4) можно также записать в виде: 8 = CD ² . (6)

В процессе продвижения по шнеку вследствие наклона оси шнека по отношению к горизонту меняется расстояние h от точки контакта стебля с валом шнека до основания стебля (на уровне поверхности поля) и соответственно меняется длина колеблющейся части подсолнечника (от точки контакта с валом до корзинки). Это значит, что жесткость С принятой расчетной модели, а также параметр являются функциями времени:

С=С ( t ) и 8 = 8 ( t ) .

Если исходить из того, что зависимость 8 = 8(t) каким-либо образом определена, иссле- дование поперечных колебаний подсолнечника при прохождении через шнек сводится к анализу решений дифференциального уравнения (3) при различных значениях частоты вращения вала шнека . Получение решения уравнения (3) аналитическими методами в случае 8 = 8(t) крайне затруднено.

Поэтому такое решение осуществлялось на основе численных методов следующим образом.

dx

Вводим новые переменные у — _x у — x — _

1         2        dt и преобразуем уравнение (3) к системе двух ференциальных уравнений вида:

dv у dt диф-

d2 = ^(t)(A sin Qt — yx), dt                         v решение которой будем искать, исходя из нулевых начальных условий:

при t = 0, y_x = 0, y₂ = 0.            ⁽⁸⁾

У1 и , У2 и искомых переменных в предыдущий момент времени  t^ определить значения этих переменных в последующий момент времени  t^+1 .

Программа расчета, реализующая на ЭВМ вычисления по схеме (9), допускает использование произвольной функции ((^ t ) . Тестирование программы было выполнено в предположении 8 = const . В этом случае легко получить точное аналитическое решение задачи о вынужденных колебаниях с нулевыми начальными условиями [3]. Анализ показал, что при выборе временного шага A t = 0,0002 с получаемое численное решение при значениях частот , типичных для реального уборочного процесса, согласуется с аналитическим решением с точностью не менее 1   .

Переходя к экспериментальной части исследования, отметим, что вместо определения жесткости с стебля подсолнечника при действии поперечной силы в зоне корзинки, целесообразно непосредственно замерять соответствующие частоты собственных колебаний    , связанные с жесткостью с формулой (5). Такие замеры можно выполнить в опытах на резонанс.

Для проведения таких опытов была создана установка, представляющая собой вибровозбудитель, способный сообщать малые поперечные перемещения гармонического типа (2) любой точке стебля, находящейся на высоте h , считая от основания стебля. Основными элементами вибровозбудителя являются электродвигатель (с устройством, позволяющим не прерывным образом изменять частоту вращения ~ его вала) и кривошипно-шатунный механизм, переводящий вращательное движение вала в возвратно-поступательное движение штока в соответствии с гармоническим законом (2) при амплитуде A = 0,003 м .

Присоединив горизонтально расположенный шток к выбранной точке с тебля (на высоте h ), включаем двигатель и постепенно увеличиваем частоту вращения его вала. Первоначально незначительные поперечные колебания растений подсолнечника, начиная с некоторого значения , заметно усиливаются и достигают критического (резонансного) уровня при совпадении частоты возмущающего воздействия с частотой (нижней) собственных колебаний исследуемой механической системы. Указанные резонансные значения фиксируем в качестве искомых (круговых) частот <—| колеб/ мин] собственных колебаний. Пересчет к угловым частотам аэ\с 1 ] осуществляем по формуле:

— ^ус

CD ----

Продолжая увеличивать — > —*), замечаем, что колебаний исследуемой собственных колебаний

.— ус

CD ---

частоту (в области амплитуда поперечных системы существенно

уменьшается, но затем при некотором значении ~ **

снова наблюдается резонанс. Тем самым фиксируем вторую (более высокую) частоту собственных колебаний исследуемой системы. Заметим, что форма колебаний при этом не соответствует расчетной схеме “масса на пружине”. При колебаниях на высших частотах большую роль играет распределенная масса стебля и его изгибные характеристики. Для подобных колебаний характерны небольшие отклонения в поперечном направлении, однако вибрации корзинки настолько интенсивны, что способны приводить к полному осыпанию семян из корзинки.

Расчетно-экспериментальные исследования с применением описанных процедур были выполнены применительно к конкретному полю подсолнечника, готового к уборке. На указанном поле были выбраны наиболее представительные образцы растений подсолнечника. С этими образцами были выполнены испытания по замеру нижней частоты собственных колебаний при фиксированных значениях высоты h в диапазоне 0,8 “ < h < 1,6 “ , который характерен для исследуемого варианта комбайна со шнековой подачей. Полученная в результате таких испытаний зависимость частоты собственных колебаний ^— от высоты h для одного из испытанных образцов подсол- нечника представлена в виде таблицы 1. Указанная таблица дает основание судить о непрерывной функциональной зависимости б— = б—( h ) для данного образца подсолнечника на основе ее пяти установленных значений ^— = _( hh ) , i = 0,1, 2, 3, 4. Аналогичные испытания по всем остальным образцам подсолнечника показали, что получаемый при этом спектр частот _ = ,—( h ) собственных колебаний пренебрежимо мало отличается от описываемого таблицей 1.

Таблица 1 - Зависимость круговой частоты СО собственных колебаний образца подсолнечника от высоты h точки приложения возмущающего воздействия

h \ м ]	0,8	1	1,2	1,4	1,6
— \ колеб / мин ]	10 8	118	14 6	18 0	26 5

В процессе испытаний было также установлено значение _ ** частоты возмущающего воздействия, которое соответствует второму резонансу (второй частоте собственных колебаний) образца подсолнечника, а именно ^_** = 500 об / мин (при h ₌ 0,8 “ ). При такой частоте возмущающего воздействия вибрации подсолнечника оказывались настолько интенсивными, что приводили к полному осыпанию семян из его корзинки. Отсюда делаем вывод, что при уборке данного поля частота вращения вала шнека не должна превышать найденного значения ____ **        ^

Q (т.е. Q <  П ).

С помощью несложного кинематического расчета при заданных значениях скорости комбайна v , частоты вращения    вала шнека, размера его шага, угла наклона оси шнека по отношению к горизонту, а также удаленности торца шнека от поверхности поля (0,8 м) можно определить в каждый текущий момент времени t расстояние h от точки касания стебля с валом шнека до основания этого стебля (считая, что при t = 0 имеет место h = 0,8 м). Соответствующие зависимости h = h (t) для трех предполагаемых вариантов скоростных режимов работы исследуемого комбайна представлены таблицей 2. Для каждого такого варианта зависимость h = h (t) устанавливается на основе заданных пяти ее значений h =h(t.), i = 0,1, 2, 3,4.

Используя найденные зависимости _. = <—( h. ) и h. = h ( t. ) , с учетом формул (10) и (6) получаем табличные значения g. = (t^ t .) искомой функции 5= £ ( t ), входящей в сформулированную динамическую модель. Непрерывный вариант таблично заданной функции g. = g^t. ) строился по схеме кусочно- линейной интерполяции

е ( t ) = ^. + ^^i ( t-t i ),        (11)

ti+1     ti t, < t < t.+1 (i = 0,1,2,3,4).

При проведении численных исследований вынужденных колебаний растений подсолнечника в процессе его транспортировки шнеком особое внимание было уделено оценке влияния длительности времени такой транспортировки на интенсивность колебаний.

По данным таблицы 2, для выбранных вариантов рабочих режимов исследуемого комбайна временной интервал транспортировки составляет величину порядка 1 с. Поэтому для расчетных вариантов с меньшими (в 2-3 раза) значениями частот    вращения вала шнека такой интервал времени принят равным 2 с.

Таблица 2 – Зависимость расстояния h (от основания стебля до точки его контакта с валом шнека) от времени t при различных режимах работы уборочного комбайна

h [ м ]	0,8	1	1,2	1,4	1,6
о Q = 367об/мин, VK = 5 км/ч	0	0,281	0,532	0,77	1
О = 421,9 об/мин, VK = 6 км/ч	0	0,256	0,499	0,736	0,969
0 = 482,2 об/мин, VK = 7 км/ч	0	0,222	0,433	0,637	0,838

На рисунке 2 представлена картина вынужденных колебаний (по перемещению x и скорости v =x ) для рассматриваемой модели взаимодействия подсолнечника со шнеком при скорости вращения вала шнека 0 = 160 об/мин и длительности колебательного процесса 2 с. Видно, что на начальном этапе процесса размах колебаний увеличивается постепенно, а ближе к концу временного интервала 2 с интенсивность колебаний резко возрастает.

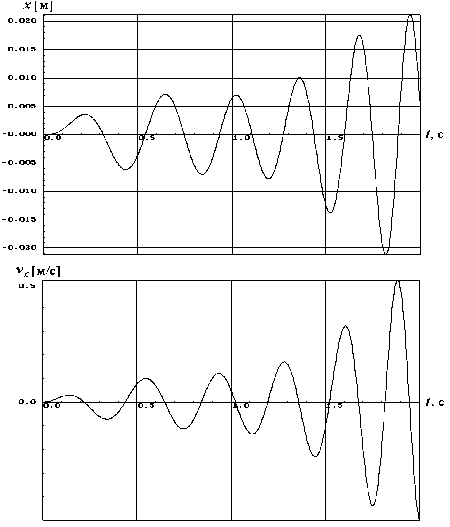
Рисунок 2 – Картина вынужденных колебаний расчетной модели по перемещению x и скорости v ₌ x при длительности колебательного процесса 2 с и частоте возмущения ~ = 160 об/мин

Здесь следует обратить внимание на тот факт, что в зоне режущего аппарата, куда подсолнечник попадает к концу процесса транспортировки шнеком, установлена фиксирующая планка. Боковой удар об эту планку колеблющейся корзинки подсолнечника со скоростью более 0,5 м/c приводит к осыпанию семян из корзинки. Поэтому рассматриваемый колебательный процесс со скоростью порядка 0,5 м/c на заключительной его стадии следует признать неприемлемым для реального уборочного режима работы комбайна.

На рисунке 3 для сравнения представлены аналогичные результаты, соответствующие ситуации, когда длительность рассматриваемого колебательного процесса сокращена до 1 с (при том же значении частоты вращения вала 0=160 об / мин ). Такого эффекта можно добиться, используя шнек с увеличенным в 2 раза размером шага. Как видно из рисунка 3, в такой ситуации интенсивность колебаний заметно снижается. При этом значения скорости колеблющейся корзинки не выходят за допустимый предел 0,5 м/с.

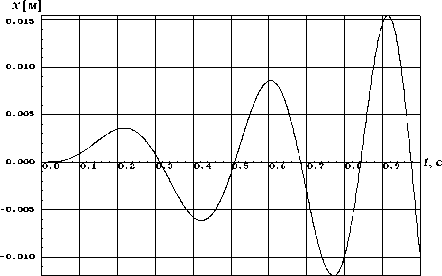
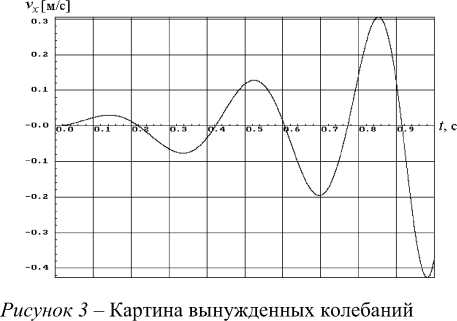
расчетной модели по перемещению x и скорости v ₌ пр при длительности колебательного процесса 1 с и частоте возмущения ~ = 160 об/мин

На рисунке 4 представлены расчетные результаты для предполагаемого рабочего варианта (см. табл. 2) при ~ = 367 об/ мин . Видно, что интенсивность колебаний в связи с более чем двукратным увеличением частоты О вращения вала шнека (от 160 об / мин до 367 об / мин ) снизилась как по перемещению, так и по скорости в несколько раз (по скорости снижение четырехкратное).

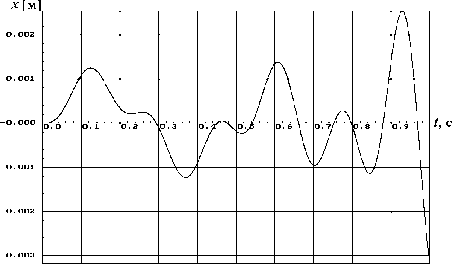
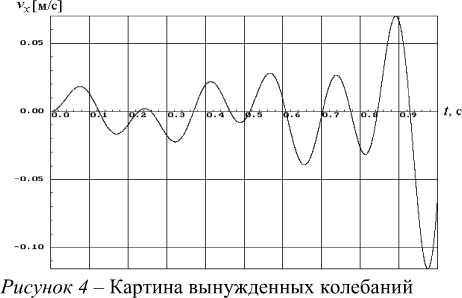
расчетной модели по перемещению x и скорости v ₌ п при длительности колебательного процесса 1 с и частоте возмущения ~ = 367 об / мин

Наглядное представление о влиянии длительности рассматриваемого колебательного процесса и частоты вращения вала шнека на интенсивность колебаний дают таблицы 3 и 4.

Таблица 3 – Максимальное перемещение и максимальная скорость корзинки подсолнечника при длительности колебательного процесса 2 с в зависимости от частоты вращения вала шнека

~ об/мин	100	130	140	150	160	170	220
v max , [м/c]	0,23	0,43	0,51	0,51	0,5	0,52	0,45
x max , [м]	0,015	0,025	0,025	0,025	0,022	0,021	0,014

Здесь для двух вариантов длительности колебательного процесса (2с и 1с) представлены максимальные значения перемещения x и скорости v    расчетной модели в зависимости от частоты

~

. Из анализа этих результатов с учетом сказанного ранее о верхнем предельном значении

~ ^~

**

частоты

вращения вала шнека следует, что надежный убо- рочный процесс с использованием исследуемого комбайна может быть осуществлен в диапазоне час- тот вращения вала шнека

~

200 об / мин     500 об / мин

Таблица 4 – Максимальное перемещение и максимальная скорость корзинки подсолнечника при длительности колебательного процесса 1 с в зависимости от частоты вращения вала шнека

~ об/мин			160	170	220	367	421,9	482,2
	v max	, [м/c]	0,42	0,32	0,19	0,12	0,06	0,07
	x max	, [м]	0,015	0,015	0,009	0,003	0,002	0,0018

При этом нижнее ограничение может быть уменьшено в случае увеличения размера шага шнека.

Представленные в таблице 2 варианты скоростного режима работы исследуемого комбайна полностью вписываются в диапазон (12) и обеспечивают наилучшую производительность уборочного процесса в рамках ограничений (12). Проведенная с использованием данного комбайна уборка отмеченного выше поля подсолнечника подтвердила выводы изложенной расчетной методики.

В завершение статьи отметим основные ее результаты.

Представлена методика определения оптимальных параметров процесса уборки подсолнечника комбайном со шнековой подачей, основанная на расчетной модели вынужденных колебаний транспортируемого шнеком подсолнечника вследствие биений со стороны вала шнека и анализе спектра частот собственных колебаний образцов подсолнечника, взятых с готового к уборке поля. Дана оценка влияния частоты вращения вала шнека и размера его шага на интенсивность вынужденных колебаний подсолнечника в процессе взаимодействия со шнеком.