Определение ожидаемого ущерба предприятия для различных вариантов частичной передачи рисков страховщику

Различные варианты управления рисками на предприятиях направлены на их снижение [4; 5]. Одним из способов управления рисками может выступать страхование от различных событий, когда предприятия, действующие в условиях промышленных и экономических рисков, могут часть ответственности по ним передать страховой организации [6; 9]. При этом страхование является одним из возможных вариантов управления риском наряду с формированием резервного фонда предприятия и предупредительными мероприятиями по снижению уровня ущерба и/или вероятности инцидента [2; 3; 7]. В данном случае необходимо оценить тот риск, который остается у предприятия, застраховавшего риск не полностью.В процессе эволюции института страхования появились различные формы страховой ответственности, позволяющие учесть интересы обеих сторон [15]. В этих условиях предприятие может застраховать свои риски, выбрав наиболее приемлемый для него вид страхования и условия договора [11; 12].

Пусть X - случайная величина, соответствующая размеру ущерба предприятия при наступлении застрахованного события, А - событие, состоящее в том, что страховой случай наступил, S - стоимость застрахованного имущества предприятия.

Математическое ожидание ущерба предприятия обозначим М(Х), рассчитаем по формуле математического ожидания для дискретной либо для непрерывной случайной величины в зависимости от характера исходных данных. Условное математическое ожидание М(Х\А) есть математическое ожидание ущерба предприятия при условии, что произошло непредвиденное событие, повлекшее за собой

ущерб [1]. Р(А) - вероятность реализации данного события. Тогда ожидаемый ущерб предприятия вычисляется по формуле [8]

• (1)    Л^^4ШфРС4).

Вероятность наступления непредвиденного события Р(А) зависит от времени, поскольку при различной продолжительности периода страхования, а также в разные моменты действия договора страхования вероятность наступления страхового события может меняться:

• (2)    Р(А)= 1_О (p^dt.

Здесь (pt) - функция плотности распределения вероятности наступления страхового события, Т - период действия договора страхования.

ИД-1) зависит:

• •    от способа распределения ответственности между страховщиком и предприятием#!'^;

• •    плотности распределения случайной величины ущерба от непредвиденного случая fix).

В качестве функций pt) к fix) могут выступать известные функции плотностей распределения вероятностей.

Таким образом, зная закон распределения случайной величины, описывающей размер ущерба при наступлении непредвиденного случая и систему страховой ответственности, описанную в договоре, можно определить ожидаемый ущерб предприятия:

• (3)    А/(.\) А/(.\|.1 )•/’(.!) j/ /(х)о€г<х)^х

Рассмотрим различные формы страховой ответственности, которые могут быть использованы предприятием при заключении различных договоров страхования. Начнем с такой формы, как страхование «первого риска». В данной ситуации ответственность страховщика ограничивается определенной страховой суммой С, При страховании «первого риска» страховая организация выплачивает возмещение предприятию, если ущерб меньше страховой суммы С, если же ущерб превышает эту сумму, тогда предприятие получит от страховщика только страховую сумму С. а оставшийся ущерб должно будет компенсировать самостоятельно. Запишем формулу для определения ожидаемого ущерба предприятия-страхователя в зависимости от размера этой суммы С:

• (4)    ’

MW/(х) Сх - C^dx.

Получили интеграл с переменным нижним пределом С [13], тем самым страхователь может, варьируя в (4) размер страховой суммы С, определить приемлемый для него размер ожидаемого ущерба.

При передаче промышленных рисков может быть использована одна из форм страхования с франшизой. Данный вариант страхования подразумевают передачу предприятием рисков, превышающих определенную сумму (fr) - франшизу. В данном случае, когда предприятие оставляет себе риски, связанные с небольшими и средними ущербами, возможны два варианта выплаты страхового возмещения. При страховании с условной франшизой предприятие берет на себя полностью ущерб, если он не превышает указанный в договоре размер франшизы (fr), в противном случае - страхователь получает полную компенсацию ущерба. Данный вид договора может быть описан следующей формулой для вьиисления ожидаемого ущерба предприятия-страхователя:

• (5)    ОДЛ^/^ fMxdx.

Для страхования с условной франшизой получили в (5) интеграл с переменным верхним пределом fr [13], с помощью которого предприятие, желающее застраховать свой риск с использованием данного вида договора, может рассчитать свой ожидаемый ущерб при различных значениях франшизы fr.

При страховании с безусловной франшизой возмещение выплачивается, если его размер превышает указанную в договоре сумму fr. при этом из величины ущерба вычитают эту сумму. То есть предприятие-страхователь, в отличие от страхования с условной франшизой, всегда оставляет на собственном удержании сумму ущерба, соответствую размеру франшизы:

• (6)    М(Х\А)= /Г fM^dx + ff_rfM frdx.

Для страхования с безусловной франшизой получили два интеграла - первый с переменным верхним, второй - с переменным нижним пределом [13], варьируя размер которых в (6) можно получить значение размера ожидаемого ущерба предприятия-страхователя.

Таким образом, при определении А/(ЛД) получили интеграл с переменным верхним или нижним пределом в зависимости от конкретной задачи. Здесь величина S является фиксированной, а величины Сир переменными. Изменяя сумму, разграничивающую ответственность предприятия и страховщика, можно варьировать размер ожидаемого ущерба предприятия. Определение ущерба, оставшегося у предприятия после передачи части риска по договору страхования, необходимо для решения задач о размере резервного фонда и о ресурсах, направляемых на предупредительные мероприятия. Размер оставшегося у предприятия риска зависит не только от границы ответственности, но и от функций распределения случайных величин, характеризующих риск.

В качестве законов распределения случайной величины ущерба рассмотрим экспоненциальный, нормальный и равномерный законы. Плотности распределения случайной величины размера ущерба от аварии или инцидента иллюстрируют особенности застрахованного риска, связанные с величиной ущерба. Экспоненциальный закон характерен для случаев, малый размер ущерба которых имеет высокую вероятность и наоборот катастрофический ущерб маловероятен. Нормальный закон описывает случаи, для которых малый и крупный ущерб имеют малую вероятность, а средний по величине ущерб наступает достаточно часто. Применение равномерного закона распределения вероятностей допустимо при описании случаев, малый ущерб которых имеет низкую вероятность появления, а крупный ущерб наступает достаточно часто.

Рассмотрим более подробно различные системы передачи риска в сочетании с различными законами распределения. Для передачи риска по системе страхования «первого риска» при нормальном законе распределения случай ной величины размера ущерба, получаем на основе (4):

Л#4)=

/_с /&)(^ ~ C)dx = ^_^ f_c е~ и¹ Qx — CJdx.

Если ущерб распределен по экспоненциальному закону, тогда из (4) получим следующее выражение:

Л/Щ4)=

J? f(x)(x ~ C)dx = Л е~^ЛхСх - C)dx.

Для ущерба, распределенного по равномерному закону для страхования предельных рисков (4) получаем:

Л/Щ4)=

// f^x} (х — C)dx = -| х(х — C)dx.

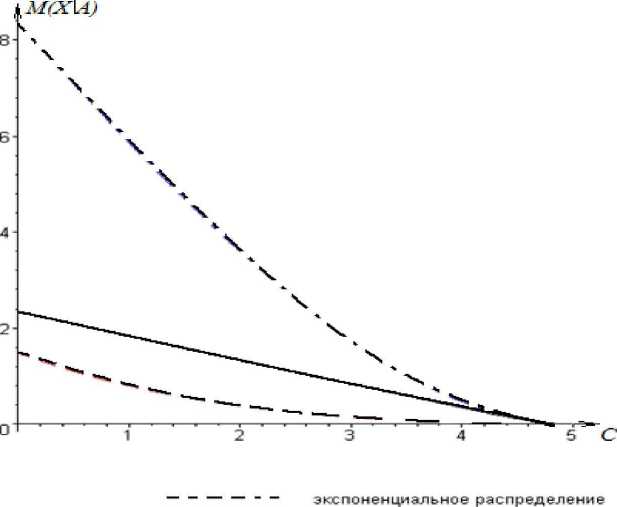
В полученных формулах для передачи риска по системе страхования «первого риска» изменяемым параметром является размер страховой суммы. Варьируя эту переменную, предприятие может оценить ожидаемый ущерб от реализации страхового случая. Изобразим полученные результаты графически для трех законов распределения величины ущерба. Примем страховую стоимость £=5 ден. ед., / 0.4. о=0,4, /77=2,5 ден. ед.

----------- нормальное распределение

---- -- равномерное распределение

Рис. 1. Зависимость ожидаемого ущерба предприятия от величины страховой суммы

Из рис. 1 видно, что наибольшая величина ожидаемого ущерба предприятия соответствует равномерному распределению. Следует отметить, что предприятие не выбирает закон распределения той или иной случайной величины - он формируется независимо от желания руководства организациии, но предприятие может выбрать, какой риск и на каких условиях передать страховой органиации. При других значениях исходных параметров распределения ущерба вид графиков остается тем же, их характер не меняется существенным образом.

Если рассматривать передачу риска по системе страхования с условной франшизой (5), тогда для нормального распределения получим следующее выражение:

ЛЙЩ4)=

//ГЛ*№ = ^

\ е за1 xdx.

-о

При экспоненциальном распределении величины ущерба получим на основе (5):

Жф|=

{'’ fWxdx = 2^

е ^Xxdx.

Для равномерного распределения будет следующий интеграл с переменным верхним пределом (5):

л#Н)=

J'; ' f(x)xdx = ^^J x2dx.

Проиллюстрируем полученные результаты для страхования с условной франшизой (рис. 2). Значения параметров распределения 5', Л ст, т - те же. что и для страхования по системе

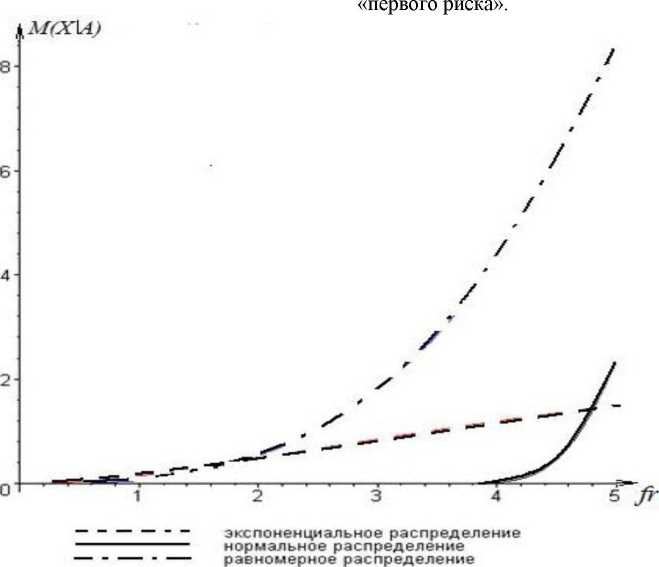
Рис. 2. Зависимость ожидаемого ущерба предприятия от размера франшизы при страховании с условной франшизой

На рис. 2 видно, что. как и для страхования по системе «первого риска», наибольший ожидаемый ущерб соответствует равномерному распределению, а нормальное распределение дает самый низкий результат.

Если рассматривать передачу риска по системе страхования с безусловной франшизой (6), тогда для нормального распределения получим следующее выражение:

МЖ)= e“ =^ xdx + ^^ L e“ ^= dx-

Для экспоненциального распределения получим с использованием (6):

' WH)=Л Г; е“ Xxxdx + Л ■ fr ff е“ Axdx.

При равномерном распределении величины ущерба будет (6):

’ Л/Щ4)=

• - х2 dx + — ff х dx.

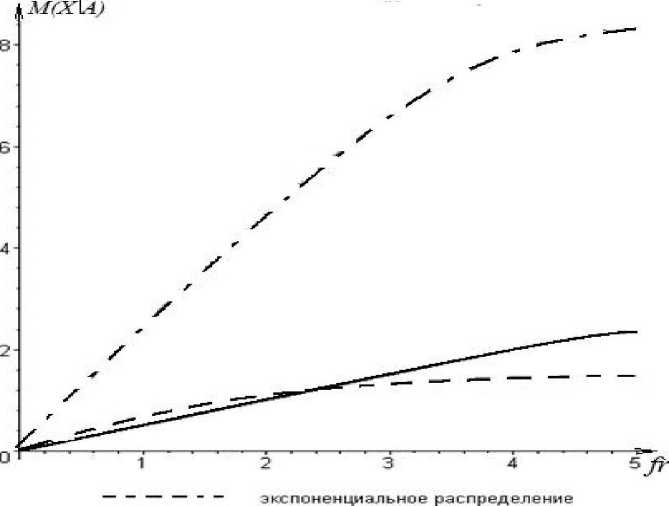
Изобразим на графике полученные результаты (рис. 3) для значений параметров S, Л ст, т, используемых ранее.

нормальное распределение равномерное распределение

Рис. 3. Зависимость ожидаемого ущерба предприятия от размера франшизы при страховании с безусловной франшизой

Как и в предыдущих вариантах передачи риска, больший ожидаемый ущерб получен при равномерном распределении ущерба случайной величины. Ожидаемый ущерб, соответствующий экспоненциальному распределению, превышает ущерб при нормальном распределении для франшизы не более половины стоимости объекта страхования, а с увеличением размера франшизы ситуация меняется.

Представленные в статье формулы позволяют определить ожидаемый ущерб предприятия для различных вариантов передачи риска страховой организации. При этом, варьируя сумму, разграничивающую ответственность предприятия и страховщика, можно подобрать условия страхования, наилучшим образом отвечающие требованиям предприятия [10, 14]. Полученные результаты дают возможность моделировать параметры договора передачи риска путем изменения величин страховой суммы (С) и размера франшизы (fr). Ожидаемый ущерб рассчитан для различных законов распределения случайной величины ущерба.