Определение параметров переходных процессов по цифровым данным

Точности определения параметров переходных процессов уделяется большое значение, поэтому оценим погрешность приближения производной синусоидального сигнала аj΄(ti) отношением разности двух рядом стоящих измерений к интервалу дискретизации, то есть аj΄(ti) = ((аj(ti)- аj(ti-1))/Δt) = Δаj(ti)⁄Δt. (1)

Исследования показали, что для уменьшения погрешности вместо приближения Δаj(ti)⁄Δt, стоящего справа от знака равенства в выражении (1), лучше использовать среднее значение двух рядом стоящих приближений, то есть следующее выражение:

аj΄(ti) = (Δаj(ti)⁄Δt+ Δаj(ti-1)⁄Δt)/2 = (аj(ti)-аj(ti-

2))⁄2/Δt. (2)

В формуле (6) [1] выражение (2) имеет вид (аj(tk/4-1) - аj(tk/4+1))/2/Δt, так как согласно алгоритму определения параметров апериодической составляющей точка аj(tk/4) фиксирована, и для увеличения точности мы вынуждены отступать от неё симметрично влево и вправо на одно измерение. Из выражений (1-2) видно, что точность приближения растёт с увеличением количества измерений k в течение одного периода, так как рост значения k приводит к уменьшению Δt – величины интервала дискретизации.

Результаты анализа погрешности, полученной заменой точного значения производной синусоидального сигнала по времени, равного ω∙cos(ω∙ti+φj), его приближением, для разного количества интервалов дискретизации k, рекомендованных [2], приведены в таблице. Во второй и третьей колонках таблицы приведены значения набольшей абсолютной погрешности, полученные заменой значения гармонической составляющей производной, равного cos(ω∙ti+φj), его приближённым значением, соответственно по формулам (1) и (2), где Δt измеряется в радианной мере Δt = πТ=π/f. Из анализа этих колонок видно, что точность приближения по обеим формулам (1) и (2) увеличивается с ростом количества интервалов дискретизации k.

Таблица. Исследования погрешности замены точного значения синусоидального сигна- ла его приближением

Значение интервалов дискретизации k	Набольшая абсолютная погрешность приближения (1)	Набольшая абсолютная погрешность приближения (2)	Отношение погрешностей	Аппроксимация погрешности приближения (2)	Относительная погрешность аппроксимации, %
10	0,309017	0,064510716	4,79	0,065063779	0,857319124
16	0,193839	0,025504642	7,60	0,025475336	0,11490357
20	0,155792	0,016368357	9,52	0,016322416	0,280669085
40	0,078378	0,004107265	19,08	0,004094771	0,304190905
80	0,03925	0,001027767	38,19	0,001027247	0,050599047
160	0,019632	0,000257001	76,39	0,000257703	0,273202159
200	0,015707	0,000164485	95,49	0,000165114	0,382354696

Также для сравнения точности приближения в четвёртой колонке таблицы приведено отношение значений погрешности, вычисленных по формуле (1), к значениям погрешности, вычисленных по формуле (2). Откуда видно, что точность приближения по формуле (2) в 4,79 раза выше для минимального интервала дискретизации k=10 и в 95,49 раза выше для максимального интервала дискретизации k=200.

В эксплуатации для каждого конкретного цифрового измерительного прибора, у которого значение k является внутренней характеристикой, можно сразу определить погрешность приближения производной синусоидального сигнала, как функции количества интервалов дискретизации k.

Этому посвящены две последние колонки таблицы. В предпоследней колонке таблицы приведены результаты аппроксимации набольшей абсолютной погрешности, полученные приближением по более точной формуле (2), выражением 6,4319 k-1,995, значения коэффициентов которого вычислены методом наименьших квадратов по данным первой и третьей колонок таблицы. В последней колонке таблицы приведена относительная погрешность этой аппроксимации, из которой видно, что для любого прибора погрешность аппроксимации не превышает одного процента.

Идентификация и определение параметров мультипликативной апериодической и постоянной составляющих.

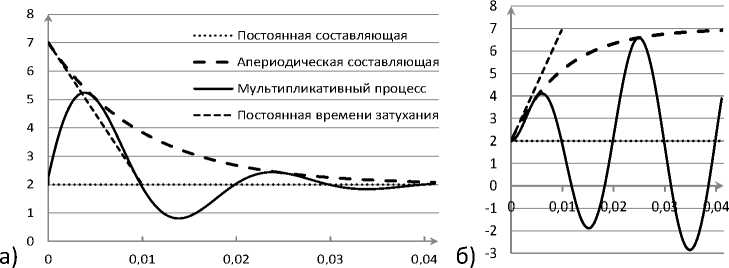
Постоянная

составляющая

Апериодическая составляющая

Мультипликативный процесс

Постоянная времени затухания

На рисунке график мультипликативного апериодического процесса видно, что ось синусоиды основного гармонического сигнала либо совпадает с осью абсцисс, когда нет постоянной составляющей, либо перемещается параллельно оси абсцисс вверх или вниз в зависимости от знака и величины постоянной составляющей, а все апериодические изменения связаны только с амплитудой основного гармонического сигнала.

При наличии мультипликативной апериодической составляющей описывается одним из следующих математических выражений:

• - для убывающей мультипликативной апериодической составляющей

аj(ti) = Xnj+AMj^exp(-ti / тмjl)•sin(юti+ф); (3)

• - для возрастающей мультипликативной апериодической составляющей

аj(ti) = ХПj+Амjf (1 - exp(-ti / тмj|)■)■sin(toti+ф), (4)

где для формул (3, 4) приняты следующие обозначения:

АмЛ, АмЛ- начальное значение убывающей и возрастающей мультипликативной апериодической составляющий, единицы измерения сигнала, В или А, тм|';. тмЛ - постоянная времени затухания убывающей и возрастающей мультипликативной апериодической составляющий, с.

остальные обозначения приведены в [1] при экспликации к формулам (1-4).

Определение постоянной составляющей сигнала при мультипликативном воздействии использует факт равенства нулю значения гармонического сигнала в точках 0±kn, где k=1,2, „., то есть при пересечении гармоническим сигналом оси абсцисс. Если текущее значение электрического сигнала в этих точках отлично от нуля, то значит, присутствует постоянная составляющая, значения которой могут быть как положительными, так и отрицательными. Приведённые далее выводы базируются на [3].

Таким образом, зная постоянную составляющую гармонического сигнала, запишем выражение (3) в виде аj(ti) - ХП = Ам|exp(-ti / тмj|)■sin(toti+ф). (5)

Учитывая, что функция sin(mti) равна единице в точках, когда аргумент принимает значения л/2±кл = N/4±kN/2, где k=1,2, .., то в этих точках выражение (5) примет вид аj(tх-N/4) - ХП = A^exp(-tx-N/4 / тмЛ), (6)

где аj(tх) - значение гармонической составляющей j-го процесса в момент времени tх, когда этот сигнал пересекает ось абсцисс, единицы измерения сигнала, В или А, аj(tх-N/4) - значение j-го процесса, которое было четверть периода N/4 назад, единицы измерения сигнала, В или А.

В уравнении (6) два неизвестных параметра Ам↓ и τм↓. Используя результат измерения в точке аj(tх-3N/4), получим второе уравнение аналогичное (6), совместно решая которые относительно неизвестных Ам; и тм; найдём их

Ам; = (аj(tх-N/4) - ХП)•exp(tх-N/4 / тм;), тм; = 0,5Т / ln( / (аj(tх-N/4) - ХП) / (аj(tх-3N/4) - ХП) / , (7)

ХП = аj(tx±nл), где n=1,2, .., где

Р/

обозначает абсолютное, то есть без учёта знака, значение некоторой величины Р,

Т - длительность периода колебаний, с, аj(tх) - значение гармонической составляющей j-го процесса в момент времени tх, когда этот сигнал пересекает ось абсцисс, единицы измерения сигнала, В или А, аj(tх-N/4) - значение j-го процесса, которое было четверть периода N/4 назад, единицы измерения сигнала, В или А, аj(tх-3N/4) - значение j-го процесса, которое было три четверти периода 3N/4 назад, единицы измерения сигнала, В или А.

Выполняя аналогичные действия над выражением для возрастающей мультипликативной апериодической составляющей (4), найдём её параметры: Ам^.- начальное значение возрастающей мультипликативной апериодической составляющей, тм^ - значение постоянной времени затухания возрастающей мультипликативной апериодической составляющей, имеем

АмТ = /( аj(tх-N/4) - ХП)

/(1-exp(-tх-

N/4 / тм;)),

τм↑ = 0,5Т / ln( ⎟ (аj(tN/4-1) - аj(tN/4+1)) / (аj(t3N/4-1) - аj(t3N/4+1)) ⎟ ),    (8)

ХП = аj(tx±nπ), где n=1,2, …, аj(tx-3k/4-1) и аj(tx-3k/4+1) – значение j-го процесса перед и после достижения трёх четвертей периода, единицы измерения j-го процесса, В или А;

все остальные обозначения приведены в экспликации к формулам (7).

Идентифицировать убывающий или возрастающий характер переходного процесса позволяет абсолютная величина следующего отношения:

⎟(аj(ti)- аj(tх))/(аj(ti-N/2) - аj(tх)) ⎟, где также все обозначения приведены в экспликации к формулам (7). На наличие убывающей мультипликативной апериодической составляющей сигнала указывает неизменное значение этого отношения, если не учитывать влияние стохастической компоненты. При возрастающей мультипликативной апериодической составляющей значение этого отношения монотонно возрастает.

В качестве примера посчитан фрагмент переходного процесса, содержащий 0,015 секунд, то есть три четверти периода Т=0,02 от его начала. Этого также достаточно для определения всех параметров, как убывающей мультипликативной апериодической составляющей, так и возрастающей мультипликативной апериодической составляющей. Параметры всех составляющих процесса такие же, что и в [1], то есть всего 98 первых измерений из N = 128 за период. Для N = 128 получим:

шаг дискретизации Δt = Т/N = 0,02/128 = 0,00015625, значения i, определяющие половину π, четверть π/2 и три четверти 3∙π/2 периода, соответственно равны N/2+1 = 65, N/4+1 = 33 и 3∙N/4+1 = 97.

Данные приведены для убывающей, согласно выражению (3), и для возрастающей, согласно выражению (4), мультипликативных апериодических составляющих при наличии постоянной составляющей. Данные получены при тех же значениях параметров, что и в [1] (в условных единицах измерения сигнала):

– постоянная составляющая АПj = 2,

– начальное значение апериодической составляющей Амj↓ = Амj↑ = 5,

– значение постоянной времени затухания апериодической составляющей τaj↓ = τмj↑= 0,01 с,

– амплитуда гармонического сигнала Аmj = 3.

Подставляя данные полученные по формуле (3) в выражения для определения параметров убывающей мультипликативной апериодической составляющей (7) получим:

τм↓ = 0,01 с, Амj↓ = 5, АПj = 2.

Относительная погрешность δ определения параметров убывающей апериодической и постоянной составляющих равна нулю. Аналогично можно подсчитать значение параметров для возрастающей мультипликативной апериодической составляющей.

Вычисленные значения параметров постоянной и мультипликативной апериодической составляющих j-го процесса дают абсолютно точный результат. Причина этого – отсутствие стохастической компоненты, обусловленной случайным характером моментов включения и отключения нагрузки.

Применение цифровой обработки данных в процессе эксплуатации при различных искажениях контролируемого сигнала в условиях не симметричной нагрузки и в критических режимах позволяет определить действительные мгновенные параметры искажения, необходимые для управления электроэнергетической системой. В нашем случае, это параметры мультипликативной апериодической и/или постоянной составляющих, полученные путём вычисления по приведённым математическим выражениям. При этом не требует ни установки дополнительного узкоспециализированного оборудования, ни создание и применение физических или математических моделей. Все действия сводится к порядку оперирования с данными, которые могут быть получены от установленных цифровых измерительных приборов, используемых для текущего измерения токов и/или напряжений в каждой фазе, и/или от регистраторов аварийных событий.

Использование дополнительного специального оборудования связано с расходами на его приобретение, установку и постоянными затратами в эксплуатации на его последующее поддержание и обслуживание. Кроме того, необходимость использования дополнительного оборудования в эксплуатации ухудшает показатели надёжности, так как известна зависимость уменьшения надёжности системы при увеличении числа её элементов. Наконец, всякое дополнительное оборудование требует решать вопросы его размещения, электроснабжения, организации сбора и передачи данных, увеличение штатной численности и др. В эксплуатации всё это и увеличивает число единиц элементов, и ухудшает экономические показатели.

Любые модели однобоки, так как они позволяют упростить сложные реальные взаимосвязи с цель «высветить» наиболее важные влияющие факторы. При цифровой обработке данных имеется возможность «увидеть» реальные значения параметров элементов системы или системы в целом в текущий момент, не прибегая к моделям и упрощениям.

К достоинствам цифровой обработки данных относится то, что с её помощью легко и качественно решаются следующие задачи:

– постоянный мониторинг параметров процесса изменения электрических сигналов во времени и/или параметров не симметричной нагрузки в электроэнергетической системе;

– увеличение быстродействия, во- и аддитивной, и мультипликативной апериодической и/или постоянной составляющих определяется практически мгновенно – меньше чем за один период, во-вторых, результаты расчётов не нужно преобразовывать в цифровой вид для ввода в систему управления объектом, так как они уже оцифрованы;

– обеспечение высокой точности определения, как параметров электрического сигнала, так и параметров искажения этих сигналов.

Выводы:

• 1.    Использование цифровой обработки данных позволяет в переходных режимах, быстро и точно определить мгновенные параметры апериодической и/или постоянной составляющих, необходимые для оценки состояния и управления электроэнергетической системой.

• 2.    Предложенные алгоритмы позволяют идентифицировать тип искажения и опре-

• делить параметры искажения гармонического сигнала любой природы (в том числе, звукового, сейсмического и др.) по результатам цифровых измерений.

• 3.    Приведены аналитические выражения для вычисления текущего значения постоянной составляющей гармонического сигнала, начального значения апериодической составляющей данного переходного процесса и текущего значения составляющих электрического сигнала.

• 4.    Предложенная технология определения параметров базируется на основе получения данных от обычных цифровых измерительных приборов, используемых для текущего измерения токов и/или напряжений, или аварийных регистраторов без использования дополнительного энергозатратного и дорогостоящего оборудования.

первых, потому, что значения параметров