Определение параметров уравнения состояния молекулярных кристаллов на основе дифрактометрических исследований

Автор: Бирюкова М.А., Ковалев Ю.М., Петров Д.В., Станкевич А.В., Шестаков М.А.

Журнал: Вестник Южно-Уральского государственного университета. Серия: Математика. Механика. Физика @vestnik-susu-mmph

Статья в выпуске: 3 т.15, 2023 года.

Бесплатный доступ

Представлены результаты определения кристаллической структуры образцов ТЭНа, гексогена и октогена методом рентгеновской дифрактометрии, приведены расчеты параметров элементарной ячейки молекулярных кристаллов, связанные с обработкой результатов рентгеновской дифрактометрии, и экспериментальные зависимости объемов элементарной ячейки молекулярных кристаллов от температуры. Полученные экспериментальные данные по изобарическому сжатию и расширению исследованных молекулярных кристаллов позволили уточнить тепловую составляющую уравнений состояния молекулярных кристаллов и получить выражение для изобарического коэффициента теплового расширения, связанное с математической моделью тепловой составляющей уравнений состояния молекулярных кристаллов. Полученная аналитическая зависимость изобарического коэффициента теплового расширения от температуры рассмотренных образцов позволяет правильно описывать предельный переход к низким температурам. Предложен метод аппроксимации, полученных экспериментальных зависимостей объема элементарной ячейки, исследуемых веществ, при изобарическом сжатии - расширении от температуры, основанный на математической модели полуэмпирических уравнений состояния молекулярных кристаллов. Данный подход позволил получить аналитическую зависимость объема элементарной ячейки кристалла от температуры, с точностью до 3 % описывающую представленные результаты рентгеновской дифрактометрии, рассмотренных в работе образцов молекулярных кристаллов.

Еще

Уравнение состояния, молекулярный кристалл, изобара, дифрактометрия, приближение дебая

Короткий адрес: https://sciup.org/147241779

IDR: 147241779 | DOI: 10.14529/mmph230308

Текст научной статьи Определение параметров уравнения состояния молекулярных кристаллов на основе дифрактометрических исследований

Необходимость расчета термодинамических характеристик различных веществ возникает всегда при решении различных задач математической физики. Поэтому построения математических моделей уравнений состояния всегда привлекало повышенное внимание исследователей самых различных специальностей [1, 2]. Несмотря на значительные успехи в развитии вычислительной техники, последовательный теоретический расчет уравнений состояния материалов методами статистической физики сталкивается с трудностями, суть которых заключается в том, что появляется необходимость корректного учета межчастичного взаимодействия. Поэтому активное развитие получили математические модели построения полуэмпирических уравнений состояния [3, 4]. Для построения полуэмпирических уравнений состояния необходимо определиться с выбором термодинамического потенциала, в зависимости от агрегатного состояния вещества. Например, для твердого тела наиболее удобным термодинамическим потенциалом является функция Гельмгольца. Далее из теоретических соображений выбирается математическая модель, позволяющая определить форму функциональной зависимости термодинамического потенциала, а коэффициенты, входящие в выбранный термодинамический потенциал, определять на основании результатов термодинамических экспериментов.

В данной работе реализован подход к определению термодинамических параметров исследуемого материала на основе прецизионных дифрактометрических исследований в широком диапазоне температур с целью уточнения вида составляющих полуэмпирического уравнения со- стояния молекулярного кристалла [5, 6] и построения уравнения, позволяющего аналитически описывать зависимость объема элементарной ячейки от температуры. Полученные экспериментальные данные позволят верифицировать тепловую часть уравнений состояния молекулярных кристаллов.

Математическое моделирование поведения объема элементарной ячейки молекулярного кристалла при изобарическом расширении и сжатии

Приведенные в работах [7-10] экспериментальные данные показывают, что в условиях ква-зиизобарического температурного воздействия изменение объёма элементарной ячейки молекулярного кристалла имеет нелинейную зависимость, которая на примере ТАТБ представлена (см. рисунок) [11] и характеризуется анизотропией силовых параметров межмолекулярного взаимо- действия.

Все попытки аппроксимации экспериментальных данных на отдельных участках экспериментальной кривой (см. рисунок) алгебраическими выражениями без учета специфики уравнений состояния молекулярного кристалла приводят к неутешительным результатам по определению зависимости коэффициента объемного расширения от температуры. Поэтому в данной работе был предложен подход, позволяющий получить аналитическую зависимость объема элементарной ячейки молекулярного кристалла от температуры и выражение для определения температурной зависимости коэффициента объемного расширения на основании уравнения состояния молекулярных кристаллов.

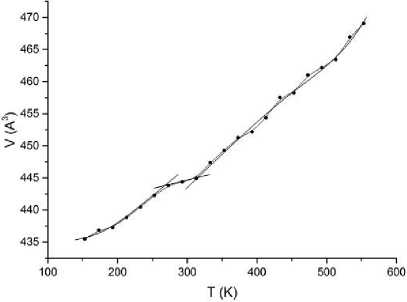
Зависимость объёма элементарной ячейки ТАТБ от температуры

Для определения зависимости объема элементарной ячейки молекулярного кристалла от температуры при изобарическом сжатии и расширении будем использовать подход, разработанный в работе [12], в приближении высоких температур.

По определению коэффициент объемного расширения а имеет следующий вид [13]:

1 (б V ) а -

V(dТ)P а связь между термодинамическими коэффициентами определяется термодинамическим равенством (аналог уравнения Грюнайзена для молекулярных кристаллов), полученным в работах [6, 12]

аС Т = y d (V)C_V d , (2)

и зависимостью коэффициента Грюнайзена [14, 15] в приближении слабого сжатия

. ( V ^

Y d = Yd — • ⁽³⁾

I Vo )

Здесь СТ - изотермическая скорость звука, yD — значение коэффициента Грюнайзена при на чальной температуре проведения экспериментов, CvD - составляющая теплоёмкости при посто- янном объёме, зависящая от деформационных (низкочастотных) колебаний молекулы и определяемая в приближении Дебая [16, 17]:

Cvd - MR 4 D ( Xd )

—

3 x_D

exp ( Xd ) — 1

- mrDc ( Xd ) , Xd - — ,

R - универсальная газовая постоянная, поделенная на молекулярную массу вещества ц ; M -число низкочастотных ( деформационных) колебаний, приходящихся на одну молекулу ТАТБ; 0 D - характеристическая температура Дебая; Т - температура тела; D ( x ) - функция Дебая , которая определяется выражением вида [16]:

D (z) - 4 ] е z0

de exp (е) — 1,

D C ( x ) - функция теплоемкости Дебая, определяемая следующим образом [16]:

DC (x) = - f ^4 x o

exp(^) d< (exP (£)-1)2

После подстановки выражений (2) и (3) в равенство (1) проинтегрируем полученное дифференциальное уравнение по температуре от значения T ₀ = 293 К до текущего значения T при постоянной изотермической скорости звука, в результате получим равенство, позволяющее определить зависимость объема элементарной ячейки V от температуры:

V = Vo /(1 - Ka (TD ( Xd ) - To D (xD))), K„ = MR (YD/CT), (4) где V0 - объём элементарной ячейки при T0 = 293 К, xD = @D / To . Аналогичный подход для опре- деления зависимости плотности ρ от температуры применялся в работе [12] для случая высокотемпературного разложения функции Дебая, и была получена зависимость следующего вида:

Д = Z ■ ц /( NV ), (5)

где N – число Авогадро, Z – количество молекул в элементарной ячейке.

Воспользоваться зависимостью (4) для аппроксимации полученных в данной работе экспериментальных данных, возможно в том случае, если удается определить значение коэффициента K_α . Покажем, что экспериментальных данных, приведенных в табл. 1–4, достаточно для определения коэффициента K_α . С этой целью воспользуемся равенством (2), которое после проведения простых преобразований можно представить следующим образом:

Ka = MR (yD/CY = «о/DC (xD), где a0 - значение коэффициента объемного расширения при температуре T0 = 293 К. Подставляя полученное выражение в равенство (3), определим уравнение для описания зависимости объема элементарной ячейки от температуры в виде

V = V o /(1 - K « (TD ( X d ) - T o D ( x D ))) = V o /(1 - « o ( TD ( X d ) - T o D ( x D )) / D C ( x D )) (6)

Зная зависимость объема элементарной ячейки от температуры (5), легко получить зависимость коэффициента объемного расширения от температуры. Подставив выражение (5) в равенство (2), получим:

a = ( a o D C ( X d )/ D C ( x D ))/(1 - « o ( TD ( X d ) - T o D ( x D ))/ D C ( x D )). (7)

В предельном случае при температуре T = 0 K равенство (6) переходит в следующее выражение

Vok = Vo /(1 + ao To D (xD))/DC (xD)), где V0k – значение объема элементарной ячейки при T = 0 K, которое для ТАТБ равно 432,185 А³ [12]. Найденное значение V0k позволяет определить плотность кристалла ТАТБ при T = 0 K, которая определяется равенством (5) и равна р0k = 1986 кг/м3. Для сравнения, значение плотности ТАТБ при T = 0 K, рассчитанное квантово-химическим методом DFT [18], приведенное в работе [19], Д)k = 1982,7 кг/м3.

Все необходимые для проведения вычислений по формулам (6) и (7) данные выбраны из работ [12, 20] и приведены в табл. 1.

Таблица 1

Параметры	Название ВВ
Параметры	гексоген	ТЭН	ТАТБ	октоген
M	12	16	12	12
^ D , К	157,83	134,44	137,30	160,15
α 0 10^–4, К^–1	1,91	2,32	1,119	1,625

Экспериментальные исследования по изобарическому нагреву и охлаждению

В данной работе экспериментальные исследования изобарического расширения (сжатия) проводились методом порошковой терморентгенографии с помощью многофункционального научно-исследовательского комплекса (МНИК) ARL X′TRA с использованием низко- высокотемпературной приставки AntonPaar TTK450, тонкоплёночного коллиматора и параболического зеркала.

В общем случае методика проведения анализа структуры молекулярных кристаллов и её уточнение для однофазных материалов по данным порошковой терморентгенографии приведена в работах [7–10]. Расчётные операции выполняются в соответствии с физическими закономерностями классической электродинамики и квантовой теорией строения вещества.

Результаты проведенных экспериментальных исследований изобарического расширения (сжатия) элементарных ячеек для гексогена, октогена и ТЭНа, приведены в табл. 2–4 соответственно. Полученные данные по кристаллической структуре указанных материалов при нормальных условиях хорошо согласуются с известными экспериментальными данными других авторов [20]. В табл. 2–4 приведены также значения рассчитанных объемов элементарных ячеек для выбранных молекулярных кристаллов ТЭНа, гексогена, октогена при различных температурах соответственно.

Таблица 2

T , K	V ex , А³	V C , А³	T , K	V ex , А³	V C , А³
153	579,796	575,420	273	591,186	591,191
163	580,339	576,683	283	591,441	592,558
173	581,393	577,958	293	593,932	593,932
183	582,120	579,242	303	595,720	595,314
193	579,344	580,536	313	597,134	596,703
203	580,609	581,839	323	598,206	598,099
213	583,386	583,151	333	599,793	599,502
223	582,963	584,471	343	601,170	600,913
233	583,639	585,800	353	602,541	602,331
243	585,801	587,136	363	603,423	603,757
253	586,735	588,480	373	605,155	605,190
263	588,175	589,832

Таблица 3

T , K	V ex , А³	V C , А³	T , K	V ex , А³	V C , А³
153	1607,932	1598,830	313	1644,653	1647,326
163	1611,374	1601,708	323	1648,119	1650,497
173	1614,187	1604,613	333	1652,242	1653,683
183	1616,058	1607,542	343	1656,162	1656,884
193	1617,559	1610,495	353	1660,121	1660,098
203	1620,933	1613,468	363	1659,709	1663,328
213	1623,047	1616,460	373	1663,574	1666,571
223	1624,442	1619,472	383	1664,780	1669,829
233	1626,790	1622,502	393	1669,763	1673,101
243	1627,498	1625,549	403	1672,316	1676,387
253	1630,192	1628,613	413	1675,445	1679,687
263	1633,372	1631,693	423	1678,106	1683,002
273	1635,652	1634,789	433	1681,234	1686,331
283	1640,582	1637,900	443	1684,898	1689,673
293	1641,027	1641,027	453	1690,062	1693,031
303	1643,731	1644,169

Данные табл. 2–4 показывают, что рассчитанные и экспериментальные значения объемов элементарных ячеек кристаллов ТЭНа, гексогена и октогена различаются не более 2–3 % во всем диапазоне изменения температур.

В табл. 5 на основании выражения (7) приведены безразмерные значения коэффициента объемного расширения а / а₀ для молекулярных кристаллов ТЭНа, гексогена и октогена в зависимости от температуры.

Таблица 4

T , K	V ex , А³	V C , А³	T , K	V ex , А³	V C , А³
153	510,913	507,414	273	517,226	517,124
163	511,880	508,193	283	518,103	517,962
173	512,049	508,979	293	518,803	518,803
183	512,638	509,771	313	520,171	520,496
193	512,785	510,570	333	521,635	522,203
203	513,935	511,373	353	523,204	523,924
213	514,095	512,182	373	525,076	525,658
223	514,414	512,995	393	525,916	527,406
233	515,279	513,812	413	527,850	529,166
243	515,563	514,634	433	528,857	530,940
253	516,084	515,460	453	530,443	532,727
263	516,788	516,290

Таблица 5

Т , К	a / a ₀
Т , К	ТЭН	Гексоген	Октоген
153	0,9423	0,9378	0,9404
163	0,9486	0,9453	0,9479
173	0,9543	0,9520	0,9544
183	0,9595	0,9579	0,9602
193	0,9642	0,9632	0,9653
203	0,9686	0,9680	0,9700
213	0,9727	0,9725	0,9743
223	0,9766	0,9766	0,9782
233	0,9803	0,9805	0,9819
243	0,9839	0,9841	0,9853
253	0,9873	0,9876	0,9885
263	0,9906	0,9909	0,9916
273	0,9938	0,9940	0,9945
283	0,9969	0,9971	0,9973
293	1,0000	1,0000	1,0000
303	1,0030	1,0029	1,0026
313	1,0060	1,0056	1,0051
323	1,0089	1,0083	1,0076
333	1,0118	1,0110	1,0099
343	1,0146	1,0136	1,0123
353	1,0175	1,0162	1,0145
363	1,0203	1,0187	1,0168
373	1,0231	1,0212	1,0190
383	1,0258	1,0237	1,0212
393	1,0286	1,0261	1,0233
403	1,0314	1,0285	1,0254
413	1,0341	1,0309	1,0275
423	1,0368	1,0333	1,0296
433	1,0396	1,0357	1,0317
443	1,0423	1,0380	1,0337
453	1,0451	1,0404	1,0358

Представленные в данной работе результаты показывают, что тепловая часть уравнений состояния [6] правильно описывает температурную зависимость объема молекулярного кристалла и может применяться с высокой точностью (менее 2 %) для аппроксимации экспериментальных данных, связанных с определением изобарического коэффициента объемного расширения.

Список литературы Определение параметров уравнения состояния молекулярных кристаллов на основе дифрактометрических исследований

Сон, Э.Е. Современные исследования теплофизических свойств веществ (на основе последних публикаций в ТВТ) (Обзор) / Э.Е. Сон // Теплофизика высоких температур. - 2013. -Т. 51, № 3. - С. 392-411.
Исследования теплофизических свойств веществ и материалов в Новосибирском научном центре СО РАН в 2002-2012 годах / С.В. Станкус, Р.А. Хайрулин, В.Г. Мартынец, П.П. Безверхий // Теплофизика высоких температур. - 2013. - Т. 51, № 5. - С. 769-786.
Хищенко, К.В. Исследование уравнений состояния материалов при высокой концентрации энергии / К.В. Хищенко, В.Е. Фортов // Известия Кабардино-Балкарского государственного университета. - 2014. - Т. IV, № 1. - С. 6-16.
Жарков, В.Н. Уравнения состояния при высоких температурах и давлениях / В.Н. Жарков, В.А. Калинин. - М.: Наука, 1968. - 311 с.
Ковалев, Ю.М. Математическое моделирование тепловой составляющей уравнения состояния молекулярных кристаллов / Ю.М. Ковалев // Вестник Южно-Уральского государственного университета. Серия «Математическое моделирование и программирование». - 2013. - Т. 6, № 1. - С. 34-42.
Ковалев, Ю.М. Уравнения состояния для описания изотермического сжатия некоторых молекулярных кристаллов нитросоединений / Ю.М. Ковалев // Инженерно-физический журнал. -2020. - Т. 93, № 1. - С. 229-239.
Исследование параметров кристаллической и молекулярной структуры дифениламина с помощью кристаллографической модели, построенной по данным порошковой дифрактометрии / А.В. Станкевич, Л.Х. Бадретдинова, Д.А. Хадиева и др. // Вестник Казан. технол. ун-та. - 2013. -№ 21. - С. 26-29.
Построение и исследование кристаллографической модели бензотрифуроксана на основе данных порошковой дифрактометрии / А.В. Станкевич, Б.Г. Лобойко, О.В. Костицын, Н.П. Тай-бинов, А.И. Ахметзянов // Доклады III Всероссийской научно-практической конференции молодых ученых и специалистов «Материалы и технологии XXI века», г. Бийск, 18-20 сентября 2013 г. - С. 131-136.
Пат. 2566399 Российская Федерация, МПК G01N 23/20. Способ определения структуры молекулярных кристаллов / А.В. Станкевич, О.В. Костицын, Н.П. Тайбинов. - № 2014115539/28, Заявл. 17.04.2014, Опубл. 27.10.2015, Бюл. № 30. - 16 с.
Crystal State of 1,3,5-Triamino-2,4,6-Trinitrobenzene (TATB) Undergoing Thermal Cycling Process / J. Sun, B. Kang, C. Xue et al. // J. Energetic Mater. - 2010. - Vol. 28, № 3. - P. 189-201.
Определение параметров уравнения состояния молекулярных кристаллов ТАТБ на основе дифрактометрических исследований / М.А. Бирюкова, Д.В. Петров, Ю.М. Ковалев, Е.Б. Смирнов, А.В. Станкевич // XV Всероссийский симпозиум по горению и взрыву. Тезисы докладов. - Черноголовка, 2020. - С. 24-25.
Ковалев, Ю.М. Определение температурной зависимости изобарического коэффициента объемного расширения для некоторых молекулярных кристаллов нитросоединений / Ю.М. Ковалев // Инженерно-физический журнал. - 2018. - Т. 91, № 6. - С. 1653-1663.
Базаров, И.П. Термодинамика / И.П. Базаров. - М.: Высшая школа, 1991. - 375 с.
Ковалев, Ю.М. Определение вида коэффициента Грюнайзена для молекулярных кристаллов / Ю.М. Ковалев // Доклады Академии наук. - 2005. - Т. 403, № 4. - С. 475-477.
Ковалев, Ю.М. Функция Грюнайзена для твердых взрывчатых веществ / Ю.М. Ковалев // Вопросы атомной науки и техники. Серия: Математическое моделирование физических процессов. - 2005. - № 2. - С. 55-59.
Жирифалько, Л. Статистическая физика твердого тела / Л. Жирифалько - М.: Мир, 1975. - 382 с.
Ковалев, Ю.М. Определение температурной зависимости теплоемкости для некоторых молекулярных кристаллов нитросоединений / Ю.М. Ковалев, В.Ф. Куропатенко // Инженерно-физический журнал. - 2018. - Т. 91, № 2. - С. 297-306.
Степанов, Н.Ф. Квантовая химия сегодня / Н.Ф. Степанов, Ю.В. Новаковская // Рос. хим. журнал. - 2007. - Т. LI, № 5. - С. 5-17.
Rykounov. A.A. Investigation of the Pressure Dependent Thermodynamic and Elastic Properties of 1,3,5-Triamino-2,4,6-Trinitrobenzene using Dispersion Corrected Density Functional Theory / A.A. Rykounov // J. Appl. Phys. - 2015. - Vol. 117. - P. 215901.
Gibbs, T.R., LASL Explosive Property Data. Los Alamos Series on Dynamic Material Properties / T.R. Gibbs, A. Popolato. - Berkeley. Los Angeles, London: University of California Press, 1980. - 479 p.

Еще

Статья научная