Определение порогового решения «улучшенного» энергетического детектора в релеевском канале зондирования спектра
Автор: Елисеев С.Н., Степанова Н.В.
Журнал: Физика волновых процессов и радиотехнические системы @journal-pwp
Статья в выпуске: 3 т.28, 2025 года.
Бесплатный доступ
Обоснование. Классическая схема энергетического детектора широко используема в составе систем зондирования спектра. Простота реализации энергетического детектора и требуемый минимум априорных данных – главные его достоинства. Развитием этих схем, не требующих усложнения алгоритма работы или дополнительных данных, является «улучшенный» энергетический детектор, сближающий его по характеристикам с когерентными видами детекторов, активно рассматриваемых в последнее десятилетие. Цель. В статье исследуется проблема определения важнейшего параметра – порога детектирования (обнаружения) лицензированного пользователя по критерию минимума суммарной вероятности ошибок 1-го и 2-го рода, легко обобщаемого на критерий минимума среднего риска, более подходящего во многих практических случаях обнаружения ситуаций занятости спектра для когнитивных пользователей. Оптимизация порога рассматривается на примере известного и хорошо изученного канала с релеевскими замираниями. Методы. Значение порога определяется на основе решения дифференциального уравнения для суммы вероятностей ошибок. Результаты. Полученное решение в форме нормированного порога является функцией одной переменной: среднего отношения сигнал/шум. Заключение. Результаты позволяют соотнести характеристики усовершенствованного детектора энергии с характеристиками классического энергетического детектора, а также детектора CFAR, удовлетворяющего заданным техническим требованиям по уровню ложной тревоги. А также подтверждают важность для любого типа энергетического детектора показателей качества оценки мощности шума в канале, таких как интервал возможных значений этой мощности и диапазон достоверных результатов зондирования.
Зондирование спектра, релеевские замирания, «улучшенный» энергетический детектор, нормализованный порог решения, оптимизация суммарной вероятности ошибки обнаружения, критерий минимума среднего риска
Короткий адрес: https://sciup.org/140312399
IDR: 140312399 | УДК: 543.42 | DOI: 10.18469/1810-3189.2025.28.3.89-93
Determination of the threshold solution for an «improved» energy detector in spectrum sensing Rayleigh channel
Background. The classical scheme of an energy detector is widely used as part of spectrum sensing systems. The simplicity of the energy detector implementation and the required minimum of a priori data are its main advantages. The development of these schemes is an «improved» energy detector, which has been actively considered in the. The development of these schemes, which do not require complicating the algorithm of operation or additional data, is an «improved» energy detector, which brings it closer in characteristics to coherent types of detectors, which has been actively considered in the last decade. Aim. The article discusses the problem of determining most important parameter-the threshold for detecting a licensed user by the criterion of the minimum total probability of errors of the 1st and 2nd kind, which can be easily generalized to the criterion of the minimum average risk, it is more suitable in many practical situations for detecting spectrum occupancy situations for cognitive users. Threshold optimization is considered using the example of a well-known and well-studied Rayleigh fading channel. Methods. The threshold value is determined based on the solution of the differential equation for the sum of error probabilities. Results. The solution in the form of a normalized threshold is a function of one variable: the average signal-to-noise ratio. Conclusion. The results obtained make it possible to correlate the characteristics with those of a classical energy detector, as well as a CFAR detector that meets the specified technical requirements for the false alarm level. It also confirms the importance for any type of energy detector of quality indicators for estimating the noise power in a channel, such as the range of possible values of this power and the range of reliable sensing results.
Текст научной статьи Определение порогового решения «улучшенного» энергетического детектора в релеевском канале зондирования спектра
Улучшенный или усовершенствованный детектор энергии (Improved Energy Detector), используемый при зондировании спектра в сетях когнитивного радио, получается из схемы обычного энергетического детектора модификацией последнего путем замены операции возведения в квадрат амплитуды принимаемого сигнала в обычном энергетическом детекторе (ЭД) на про- извольную положительную степень p.
В классической постановке задача зондирования спектра формулируется как задача обнаружения сигнала первичного пользователя (ПП) по сигналам, наблюдаемым вторичными пользователями (ВП), что, в свою очередь, представляет для каждого i -го ВП задачу статистической теории проверки бинарных гипотез [1; 2]:
I W i ( t ) при н H о y i ( t) = 1 . . „ ’ '
I S i ( t ) + W i ( t ) при H H i
где y i ( t) - сигнал, принимаемый i -м ВП на интервале зондирования T ; w.^ ( t) - сигнал помехи типа белый гауссов шум (БГШ) с параметрами (0, ^ П ); S i (t) - сигнал ПП, принимаемый i -м ВП; H о - состояние радиоканала в отсутствие сигнала s(t ); H 1 – состояние радиоканала при наличии сигнала s(t ); SNR = ^ 2 / ^ П - среднее значение отношения мощностей сигнал/шум.
-
1. Описание усовершенствованного детектора энергии
В этой статье сети когнитивной радиосвязи принимают решение о присутствии или отсутствии первичного пользователя, используя усовершенствованный детектор энергии, структурная схема которого показана на рис. 1.
Решение выносится сравнением Y(T) - выходного сигнала усовершенствованного детектора энергии (УЭД) – с пороговым значением схемы решения X. Улучшенный или усовершенствован-
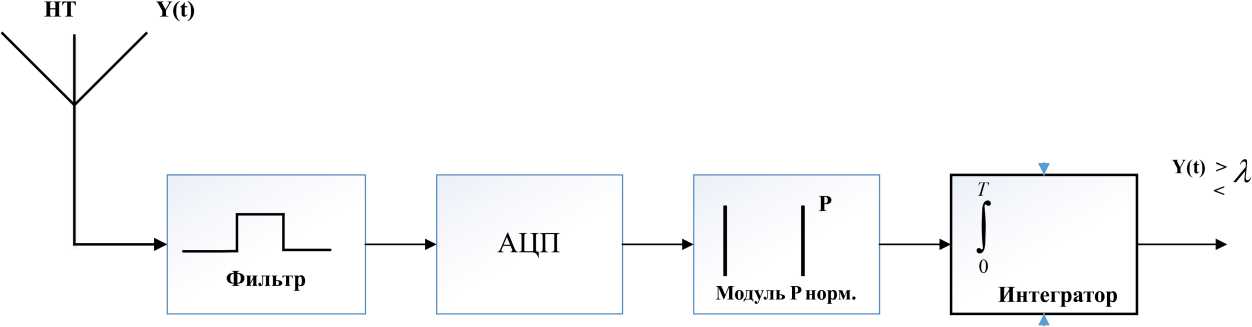
Рис. 1. Структурная схема усовершенствованного детектора энергии
Fig. 1. Block diagram of the improved energy detector
ный детектор энергии (Improved Energy Detector), используемый при зондировании спектра в сетях когнитивного радио, получается из схемы обычного энергетического детектора модификацией последнего путем замены операции возведения в квадрат амплитуды принимаемого сигнала в обычном ЭД на произвольную положительную степень p .
Цель перехода к усовершенствованному детектору энергии – сблизить характеристики некогерентного ЭД с характеристиками когерентного детектора, не требуя при этом каких-либо дополнительных априорных сведений ни о природе источника сигнала, ни о радиоканале [3].
В этом усовершенствованном детекторе энергии вместо возведения полученной выборки y i ( t ) в квадрат используется произвольная операция с положительной степенью р > 1 модуля этой выборки. По сравнению с обычным детектором положительное влияние нового детектора энергии на характеристики обнаружения может быть вызвано тем фактом, что операция возведения в квадрат в ЭД может привести к занижению составляющей сигнала в выборке при большом SNR и к завышению составляющей сигнала в выборке при малом SNR .
2. Методика расчета оптимизированного значения нормализованного порога
В работе [1] рассмотрено применение УЭД для обнаружения сигнала, удовлетворяющего условиям (1): по обоим вариантам истинности гипотез H 0 и H 1 принимаемый сигнал является гауссовским, и для каждого вторичного отличается только дисперсией: по гипотезе H 0, дисперсия равна с n , а по гипотезе Н^ , дисперсия равняется с s +с n . После некоторых алгебраических преобразований в [1] получены выражения для Y – плотности
случайной величины на выходе УЭД ( Y = | y i |Р), по гипотезам Н о и Н 1 , проинтегрировав которые получают согласно [3, (13) и (14)], что соответству-
ет в (2) Р лт - вероятности «ложной тревоги» и в (3)
Р пц - вероятности «пропуска цели»:
Г1 X 2 ' р ^
Р лт
Р пц
+»
f f Y\H о ( У*У =
X
X f fY|H1(У )dy = 0
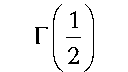
[ 1 X 2 ' р ]
WhcW
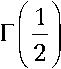
где Г ( .,. ) - неполная верхняя гамма-функция [4,
с. 60-62]; у ( .,. ) - неполная нижняя гамма-функция
[3, с. 60–62].
В литературе по специальным функциям, и частности в [4, с. 70], показана связь неполной гамма-функции с функцией ошибок, именуемой также erf ( x ):
2 2 j 1 Г1 2 1
erf ( x ) = —^ e t dt = —=y , x 2 . (4)
Vп 0 4n2 2 J
В соотношении (4) и далее учтено, что Г(1'2) = = д/п.
Если ввести в рассмотрение дополнительную функцию ошибок
erfc ( x ) = 1 - erf ( x ) =
от
4 f
4 п x
e - t 2 dt ,
а также учесть, что, согласно [3]:
erf ( x ) = 1
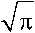
и
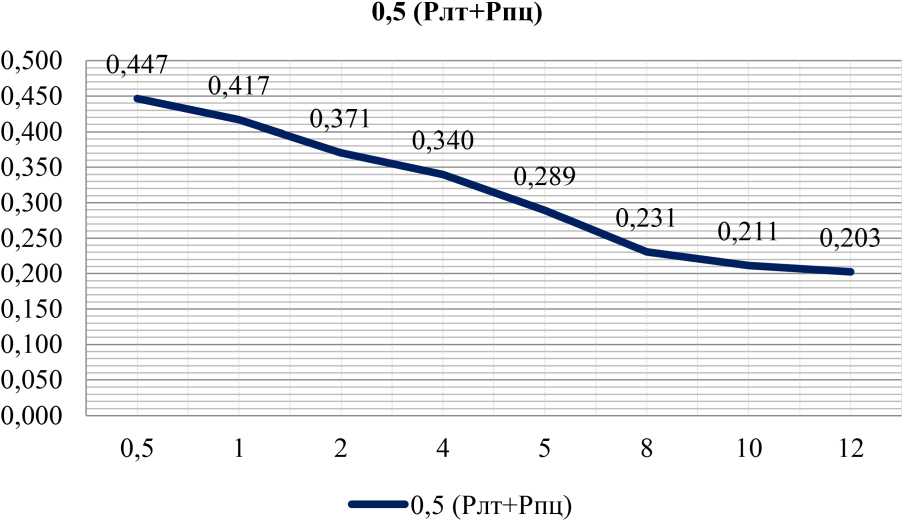
Рис. 2. График зависимости суммарной вероятности ошибки обнаружения от SNR
Fig. 2. Graph of the dependence of the total probability of detection error on SNR
1 I 1 2 I 1 J 1 2 1 .
—j= yl , x2 l + -=rl , x2 1 = 1,
После подстановки (9а) в (13) имеем:
в конечном итоге получаем для вероятностей (2) и
(3) расчетные формулы:
р лт( x ) = 1 - erf ( x ), (8)
= SNR+1 in SNR+R
2 SNR
2° n
Р пц = erf [ x ], (9)
4 ^ m J
где
X11 p 1 x = Г ’
V 2 ° n
m =
° s- +1 = SNRr+a . ° n
(9а)
Результирующая величина ошибочного обнаружения сигнала PU равна:
P e = P (H 0 ) Р лт( x ) + P (H 1 ) р пц( x ). (10)
Поскольку вероятности событий P ( H о ) + P (H) = = 1 и эти вероятности не имеют обоснованных предпосылок задания их численных значений, зададим P ( H 0 ) = P (H 1 ) = 0,5.
Тогда (10) может быть записана как
По своей природе системы когнитивного радио с динамическим доступом к ресурсам радиочастотного спектра предполагают неравную стоимость или значимость ошибок обнаружения: цена ошибки 2-го рода, т. е. необнаружение первичного пользователя, должна быть выше, чем ошибка ложной тревоги. В этом случае в оптимизируемое выражение, которое интерпретируется как значение среднего риска обнаружения [5; 8], вводятся весовые коэффициенты ошибок: C 1 и C 2 для ошибок первого и второго рода соответственно, учитывающие наряду с вероятностями P ( H 0) и P ( H 1) показатели цены ошибок (рис.2). Тогда, повторив описанную выше процедуру определения величины порога по критерию минимума среднего риска R ( x ): R( x ) = C 1 P nT( x ) + C 2 P n4( x ), (15) получаем решение для (15) в следующем виде:
Pe ( x ) = 0,5
1 - erf ( x ) - erf l —j=
. I I fm JJ
x 2
m m -1
11 1 C 1
—in m + in—
2 C 2 J
Для поиска оптимального значения переменной х приравняем к нулю значение первой производной (11):
Поскольку в большинстве практически важных случаев C. > C2, то значение порога имеет смысл только при условии dPe (x) dx
= 0,5
~r e J n
- x
+Tem T n mm
J
= 0.
1 C
—in m + in 1 > 0.
2 C 2
Решая уравнение (12) относительно переменной x 2 , после логарифмирования получаем:
m x2 =----- m -1
Заключение
Выражение (14) оптимизированного значения нормализованного порога демонстрирует результаты, идентичные значениям порога решения
p
4pt ' n2 (m )|n(m)/SNR У2, opt n полученного в [6], как частный случай разнесенного приема с селективным комбинированием в релеевском канале. Положив в (14) р = 2 (случай классического энергетического детектора), имеем хорошее совпадение с результатом в [7]. Графики зависимости суммарной вероятности ошибки обнаружения (11) для оптимизированного значения порога (14) в зависимости от SNR приведены на рис. 2.
