Одной из актуальных проблем современной газодинамики являются вопросы определения расходов газа через различные каналы при изменении относительного противодавления за каналом в широком диапазоне с привлечением минимального количества экспериментальных данных и приемлемой погрешностью [1]. В настоящее время универсальной формулы, определяющей расход газа через канал с приемлемой погрешностью при изменении режима течения газа от дозвукового до критического, не существует. Так, в работах [2-4] приводится формула, в которую необходимо подставить критическое отношение давлений и критический коэффициент расхода, а это не всегда представляется возможным.

Для получения формулы представим расход реального (вязкого) газа в следующем виде:

µ = ^{G д} = G s

^C срр v s

⋅

C s   v m _ср

где G _д , G _s - действительный и теоретический (изоэнтропийный) расходы газа, соответственно;

C _срр , C _s - среднерасходная и теоретическая скорости газа соответственно;

v _m , v _s - средний и теоретический удельные объемы соответственно.

ср

Обозначим:

v срр = ϕv  - средний коэффициент удельного объема, vs          р срр = ϕ - среднерасходный коэффициент скорости.

_Сs      срр

Тогда формула (1) запишется следующим образом:

µ=

ϕ срр

ϕ _v m ср

Рассмотрим движение реального газового потока через канал при неравномерном поле скоростей на выходе из канала. Для этого разобьем газовый поток таким образом, чтобы в каждом слое выполнялось равенство pvm = const, где pi, vt, in - давление, удельный объем, показатель политропы газа в i-м слое, соответственно. Запишем уравнение для определения политропной скорости газа

C m

2m m -1

0,5

'          m — I ]

Р 0 v 0 ¹ — C am

V        )_ и ее изоэнтропийной составляющей

C

sm

2k p0v0 k -1

0,5

m - 1 \

¹ - C am

V        )_

Отношение изоэнтропийной составляющей С к самой политропной скорости С назовем политропным коэффициентом скорости и обозначим его следующим образом:

^ m

C sm C m

k m - 1

--- k -1 m

где k – показатель изоэнтропы;

p

£ = -a- - относительное противодавление за каналом.

p ₀

Из уравнения (3) получим формулу показателя политропы

m =

-

k - 1 k

^ m

- 1

Очевидно, что показатель политропы определяется не только отношением теплоемкостей идеального газа, но и отношением скоростей, характеризующих потерю кинетической энергии в данном слое газового потока. Главным фактором в определении показателя политропы является определение политропного коэффициента скорости, который зависит от поля скоростей на выходе канала.

С понижением давления за каналом скорости газа по слоям потока увеличиваются, и при некотором давлении за каналом в одном из слоев параметры газа достигают критических значений и остаются неизменными с дальнейшим понижением давления за каналом.

По мере увеличения скорости газа по слоям потока увеличивается и среднерасходная скорость газа. Когда в пристенном слое газа скорость достигла критического значения и образовалась ЗЗП, среднерасходная скорость потока достигла критического значения, а среднерасходный коэф-

С*

фициент скорости - ^’ = срр = 1. Более срр    Сs подробно об этом изложено в работе [5].

Таким образом, при критическом режиме течения газа через канал среднерасходный коэффициент скорости равен единице. С увеличением относительного противодавления за каналом са расход газа через канал уменьшается, уменьшается и среднерасходный коэффициент скорости, и при £а «1 среднерасходный коэффициент скорости равняется политропному коэффициенту скорости пристенного слоя, т.е. Рсрр = Ртк .

Примем в первом приближении, на основании опытных данных, что среднерас- ходный коэффициент скорости при изменении относительного противодавления от £ = 1 до £ = £* изменяется по линейному закону. Тогда эта зависимость выразится формулой.

Р срр = Р тк

, , 1 - Ртк  1 - £а

1 +

Р тк    ¹ - ^£ к

где £ — критическое отношение давлений пристенного слоя.

Таким образом, для определения среднерасходного коэффициента скорости необходимо знать только политропный коэффициент скорости пристенного слоя газа в канале.

Из формулы (1) средний коэффициент удельного объема р равен отношению удельных объемов, которые определяются из уравнения политроп своего слоя, т.е.

Р т ср

v m ср

v _s

1 k

^£ s

1 mсс .

^£ т ср

В уравнение (6) входят параметры разных слоев газового потока. Для получения аналитических зависимостей между параметрами разных слоев газового потока за- пишем уравнение политропных скоростей для этих слоев и сравним их между собой. В результате этого получим следующее:

к—1т1

km

£s= тср—1

= £ т ср ^£ т ср

т к —1

mk

^£ к

и затем т 1—1 k

m 1

^£ s     ^£ т 1

k-1

тср—1 к mср k-1

^£ т ср

т к — 1 к

— mk k-1

= ^£ к       *

Но из уравнения (3)

т — 1

k

♦

m

к — 1

= Р^ т

. Тогда получим

р гPm1

^£ s    ^£ т 1

₌ г^р 2р ₌ г к

^£ т ср    ^£ к ,

где £, £ J, £тсо, £ — относительные s m mср противодавления изоэнтропийного, первого, среднего и пристенного слоев соответственно.

В формуле (6) относительное противодавление приведем к одному основанию £ = £ , используя формулы (4) и (7). После некоторых преобразований получим

P v

m ср

_ ртк

^£ а

—

\

р г тср у

.

Выражение формулы (8) и есть средний коэффициент удельного объема, но только для газового потока, в котором имеется изоэнтропийное ядро. Чтобы выражение (8) было универсальным, введены понятия параметров газа первого слоя, которые обозначается smj, фтХ и т.д. Первым слоем газового потока назван тот слой, в котором впервые возникли критические параметры в канале [5]. Тогда формула (8) примет вид

Vv mср

v mср v1

,22 G-2-/п-2 'I фтк ^ фт 1 фтср J

Z

(8')

Отличие формул (8) и (8') заключается лишь в первом члене скобок показателей степени. В уравнении (8) этот член равен единице, в уравнении (8') - ф-2. В первом случае в газовом потоке имеется изоэн-тропийное ядро, поэтому z = £s, и, как следствие, фт1 = 1. Во втором случае нет изоэнтропийного ядра, z < Z и Vi < 1. В целом уравнение (8') является универсальным для всех газовых потоков в каналах.

Для определения среднего коэффициента удельного объема по формуле (8') остается неопределенным средний политропный коэффициент скорости фс . В первом приближении примем, что политропный коэффициент скорости газового потока по радиусу канала изменяется по закону ai

Ф тг = Ф т 1 • Л ,

а относительная координата пристенно го слоя ук = 0,005 , где у. = —, у, - рас-iR стояние от стенки канала, R – радиус кана- ла; a – показатель степени координаты i-го слоя газа.

Тогда уравнение (9) для пристенного слоя газа запишется в следующем виде:

ф , —ак mk

(9')

= y k Ф т 1

Прологарифмируем выражение (9') и из него определим показатель степени пристенного слоя

₌ ln ⁽Фтк'ф_т 1 ) ln y _k

Из выражения (10) следует, что на оси газового потока показатель степени а1 = 0. Изменения показателя степени координаты газового потока по радиусу канала вы- ражается уравнением а; = ак (1 - у;). Подставим это в уравнение (9) и получим закон изменения политропного коэффициента скорости по радиусу канала

—ак (1 - yi )

Ф тг = Ф т 1 У г

Для подтверждения работоспособности формулы (11) воспользуемся эксперимен- тальными данными работы [6] для трубопровода l/d = 49 .

Из рис. 1 видно, что совпадение экспериментальных данных и расчетных по формуле (11) удовлетворительное. Для определения среднего значения политропного коэффициента скорости ф между фт1 и Фтк при изменении относительного радиуса канала y от 1 до 0,005 необходимо взять интеграл от функции (11). Но ин-ak (1-yi)

теграл от функции y     не берется. По- этому решим эту задачу с привлечением приближенных методов. В частности, на графике функции (11) проведем прямоугольник таким образом, чтобы его площадь была равна площади, образованной кривой функции (11) и осью абсцисс. Отсюда найдем зависимость между фтс , pmi и Фтк . Она определяется следующим образом:

Ф т ср = 0,75 ф т 1 + 0,25^ .

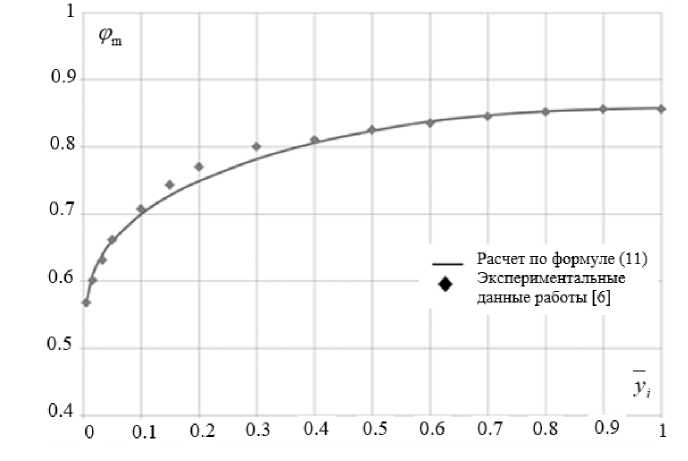
Рис. 1. Распределение поля скоростей по радиусу трубы l/d = 49

Таким образом, определена величина Рте р, которая необходима для вычисления среднего коэффициента удельного объема по формуле (8'). Подставив в формулу (2) значения ее составляющих по формулам

• (5)    и (8'), получим зависимость для определения коэффициента расхода канала при изменении относительного противодавления от единицы до критического отношения давлений:

  Ф срр V =

  P v m ср

  
  

  _ _с^фтк   ^-2 _т^-2

  ^ а   \ ^ф т ср   ^ф т 1 ) ^ф тк

  
  

  ¹ - ^ф тк ¹ - ^£ а

  1 +----г

  Ф тк   ¹ - ^£ к.

  
  
  
  

При достижении относительным противодавлением значения критического отношения данного канала, то есть £_а = £_к , среднерасходный коэффициент скорости

Р рр равняется единице, а коэффициент расхода газа через канал достигает своего максимального значения, то есть критического, и определяется формулой

*        *

V = £к

2  / -2   ,-2 > фтк^тср фтР

Для получения количественных значений величин по формулам (13) и (14) необходимо знать только величину политропного коэффициента скорости пристенного слоя данного канала. Для подтверждения правильности формул (13) и (14) приведем экспериментальные данные работ [1-4] и нанесем их на график функции (13).

Из рисунка 2 видно, что совпадение экспериментальных и расчетных данных по формуле (13) удовлетворительное. Таким образом, формула (13) является единой во всем диапазоне изменения относительного противодавления, то есть универсальной.

Кроме того, формула (13) является общей для каналов различной геометрии. На рис. 2 приведены экспериментальные данные следующих каналов: кольцевая щель, отверстие, конические сопла, лемнискат-ное сопло. Критическое давление этих каналов изменяется от s * = 0,1 - кольцевая щель до s * = 0,4 - лемнискатное сопло. Это и позволяет утверждать, что формула (13) является универсальной формулой для определения расхода газа при изменении относительного противодавления от s_fl = 1 до ^s a = 4 .

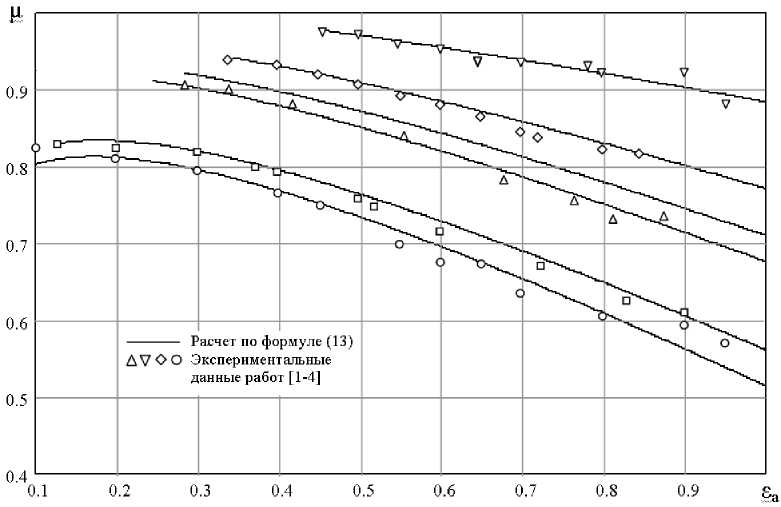
Рис. 2. Изменение коэффициента расхода газа через различные каналы * при изменении относительного противодавления от s_a = 1 до s_a = s_k

Выводы

• 1.    Получена универсальная формула для определения расхода газа через различные каналы при дозвуковых, смешанных и звуковых режимах течения газа.

• 2.    Усовершенствован показатель политропного процесса, который включает в себя не только отношение теплоемкостей

• 3.    Определены средние параметры газового потока в канале.

идеального газа, но и отношение скоростей в газовом потоке. Это позволило впервые однозначную связь между полем скоростей газового потока в канале и его критическими параметрами.