Определение реологических параметров незатвердевших бетонных смесей в процессе их заглаживания дисковым рабочим органом

Приведены методы определения реологических параметров незатвердевших бетонных смесей, конструкция экспериментальной установки и результаты реометрических исследований. Приведен вывод аналитических зависимостей для определения режимов бездефектного заглаживания свчежеотформованны.х бетонных поверхностей дисковыми, вчиковыми и брусовыми рабочими органами заглаживающих машин.

Реализация технологий отделки поверхностей пластичными материалами основывается на исследованиях физико-механических характеристик и реологических свойств

материалов, а также параметров режима отделки, определяемого конструкцией и кинематическими характеристиками рабочих органов бетоноотделочных машин.

Основным реологическим параметром незатвердевшей бетонной смеси, определяющим возможность и качество отделки, является ее вязкость, для измерения которой применяют вискозиметры.

Среди существующего многообразия методов измерений и типов вискозиметров наибольшее применение имеют ротационные и капиллярные приборы и методы.

Важная особенность ротационных вискозиметров зак

Ротационные вискозиметры подразделяются на приборы, в которых измерения выполняются при постоянном моменте, приложенном к одной из измерительных поверхностей, либо при постоянной скорости деформирования (вращения одной из измерительных поверхностей).

Часто используются одноцилиндровые ротационные вискозиметры, в которых внешний цилиндр отсутствует [7]. Они погружаются в различные точки исследуемого объема и производят измерение момента сопротивления вращению. Касательное напряжение сдвига т и вязкость Ц определяются по формулам:

M т =-----Г, 2п hr2

лючается в том, что при измерении вязкости в них можно

т

Ц = А, ГО

параллельно измерять и другие реологические характеристики, такие, например, как упругость, ползучесть, релаксацию напряжений, сдвиговую прочность, тиксотропию и др. как в ньютоновских, так и в неньтоновских средах. В ротационных приборах определение реологических характеристик осуществляется путем вращения коак

„ 4пщ где ГО =---, ф - угол наклона графика логарифмичес- tg Ф кой зависимости крутящего момента M от угловой ско рости щ вращения цилиндра: ln M = f (ln го).

Приборы, в которых определение реологических ха

сиально расположенных цилиндров.

Этот метод получил наибольшее распространение [1-6].

Пластическая вязкость определяется из уравнения

Рейнера-Ривлина:

щ = —

M ( 1

Ц pl L 4 п h ( r

^^^^^^в

2 R 2

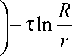
где щ - угловая скорость вращения одного из цилиндров;

R, r - соответственно радиусы внешнего и внутреннего цилиндров; h - длина погруженной части внутреннего цилиндра; - M - крутящий момент; ц _ре - вязкость пластическая; т -пределтекучести.

Уравнение справедливо, когда течение материала про

исходит во всем зазоре между внутренним и наружным

цилиндрами, а именно:

M 0 >  2 п hR ² т ,

где М0 - момент на стенке наружного цилиндра.

В случае 2 п hr ² т <  M 0 <  2 п hR ² т в уравнение (2) вместо R необходимо подставить

R о =

M . 2 п h т

При т = 0 уравнение преобразуется в уравнение

Моргулиса для ньютоновской жидкости:

M ( 1   1 )

Щ =-------I —;--- л ^,

2 п h ц ( r ² R ² J где Ц - вязкость ньютоновская.

рактеристик осуществляется путем вращения поверхностей в виде конус-конус, конус-плоскость, сфера-сфера, кольцо-кольцо, диск-диск.

В рассматриваемом случае для адекватности с процессом заглаживания дисковыми рабочими органами целесообразно использовать последнюю конструкцию с учетом специфики рабочего процесса. Схема установки, на которой проводились реометрические исследования, включает рабочий орган диск, который вращается посредством двигателя постоянного тока, установленного на раму электромагнитного вибростенда (рис. 1). На вибростоле закреплен стакан, в который помещалась исследуемая смесь. Приводной диск радиусом R устанавливался на поверхность бетонной смеси. Изменение частоты вращения диска осуществлялось традиционным методом путем изменения напряжения. Посредством аппаратуры, включающей мультиметр ИТ-60А и интегрированную в компьютер плату АЦП.

С использованием программы Excel регистрировались и рассчитывались результаты исследований по изучению характера течения пограничного слоя бетонной смеси.

Исходные данные: радиус диска R = 0,025 м; диапазон изменения параметров вибрации: амплитуда колебаний А =(0,05_0,2)-10 3 м, частота колебаний щ0=(100.. .600) рад / с, интенсивность вибрирования А2щ03 =10^50 м2/ с3; частота вращения диска щ = 10^120 рад / с; состав смеси

(цемент : песок с размером фракций менее 2,5 мм) Ц: П = 1:3, жесткость Ж4 = 60 с.

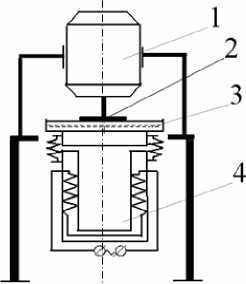
Рис.1. Схема установки: 1 - привод; 2 - диск; 3 - стакан с бетонной смесью; 4 - злектромагнитный вибровозбудитель

Рассмотрим задачу о движении вязкой жидкости в зазоре величиной h между неограниченными плоскостями, из которых нижняя неподвижна, а верхняя вращается с постоянной угловой скоростью Щ.

Предполагаем, что единственная отличная от нуля компонента линейной скорости может быть представлена в виде:

v = r Щz (z), где toz - переменная по толщине зазора угловая скорость.

Из граничных условий для v при z = 0, v = 0; z = h, v = щ r имеем граничные условия для: щ _z = to _z ( z ) : при z = 0, Щ _z ( z ) = 0; z = h, Щ _z ( z ) = to                       (8)

В анализируемом случае h - толщина пограничного слоя.

Рассматривая уравнение равновесия цилиндрического слоя получим выражение для единственного отличного от нуля компонента касательного напряжения

Т = Т ( r ) ,     = 0 .

d z

Скорость сдвига в плоских слоях жидкости может быть определена по формуле:

d v    дщ,

--= r—- .

д z     д z

Для случая ньютоновской жидкости имеем: dtoz

П r / = Т. о z

Вследствие равенства (9) правая часть уравнения (11) не зависит от z, следовательно, не зависит от z и левая часть, откуда следует:

щ _z = C 1 z + C ₂ .                 (12)

Удовлетворяя условиям (8) для Щ _z , легко определить произвольные постоянные С₁ и С₂, откуда

Щ z = Щ z .                  (13)

h

Подставляя выражение (13) в уравнение (11), получим выражения радиусов для касательного напряжения r

Т = ^Щ-.(14)

h

Момент сопротивления вращению приводного диска подсчитывается по формуле

M = 2nJТr2dr .(15)

Для случая ньютоновской жидкости с учетом (14) ,, ппщR4 имеем M =

2 h

В работах А. В. Болотного, И. Н. Ахвердова и других авторов [8-14] установлено, что при обработке свежеуло-женных бетонных поверхностей толщина пограничного слоя h может быть принята равной (0,01.. .0,05) ■ 10³ м.

Специфическая особенность различных видов строительных материалов состоит в том, что вследствие сильно развитой поверхности раздела фаз поверхностные явления в таких гетерогенных системах приобретают решающее значение по сравнению с другими видами связей. По этой причине эффективное управление свойствами дисперсных систем должно основываться, как отмечалось выше, на сочетании механических воздействий (сдвиговых деформаций, вибрации и т. п.).

Развитие представлений об управлении свойствами дисперсных систем с помощью вибрационных воздействий связано с созданием раздела реологии дисперсных систем - виброреологии. В основе виброреологии лежит изучение закономерностей деформации и течения дисперсных систем при воздействии на них вибрации.

Работы П. А. Ребиндера, Н. В. Михайлова, С. К. Носкова, Н. Б. Урьева, П. Ф. Овчинникова, А. Е. Десова, В. А. Кузьмичева и других авторов [15-26] посвящены описанию поведения полидисперсных систем в условиях вибрации и дали направление для создания нового раздела реологии - виброреологии.

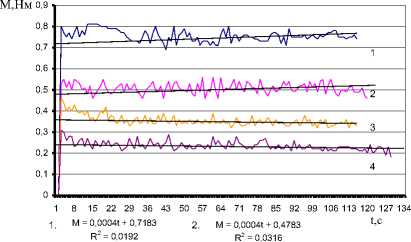
С учетом анализа исследований вышеперечисленных авторов представлены результаты реометрических исследований изменения момента сопротивления вращению диска при взаимодействии с бетонной смесью от времени (рис. 2, а, б).

В результате обработки результатов экспериментальных исследований получены зависимости изменения момента сопротивления вращению и касательного напряжения сдвига от угловой скорости вращения, представленные на рис. 3,4.

Анализируя полученные зависимости можно сделать вывод, что при вибрационных воздействиях поведение пограничного слоя при деформировании в условиях сдвига с достаточной степенью точности с позиций реологии может быть аппроксимировано моделью Ньютона: Т = ру. При этом по мере увеличения интенсивности вибрирования аппроксимация становиться более тесной.

В результате проведенных реометрических исследований с учетом и = 1 уточнено условие, выполнение которого позволяет обеспечить неразрывность потока материала в пограничном слое и, тем самым процесс бездефектного заглаживания. Для валковых и брусовых заглаживающих машин он имеет вид

О, ^{95 и} _;h < Q ( x ) = — ^Uimax( xy ) +^U 1max( zy ) ' ^y 0( x ) ⁺

1                                     ;(16)

+ 24 U2max • У0(x) 0, 05U,h для дисковых:

У0 2n

= J J v2 r max(V) 00

0,95 u , h <  Q r =

^^^^^^B

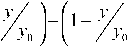
d Ф dy < 1,05 u _;h .⁽¹⁷⁾

а)

М= -0,00011 + 0,3589

R2 = 0,0086

М= -0,00011 + 0,2408 R2 = 0,0202

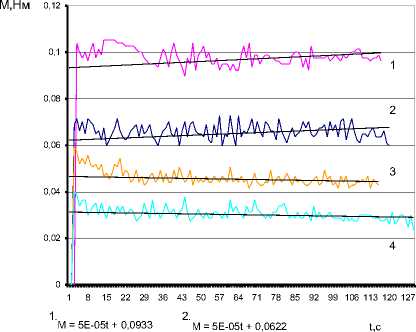
б)

R2= 0,0192

М = -2E-051 + 0,0467 R2 = 0,0086

R2 = 0,0316

М =-2E-051 + 0,0313 R2 = 0,0202

Рис. 2. Типовые диаграммы зависимости момента сопротивления вращению диска от времени: параметры: интенсивность вибрирования: а - А² ® ³ = 12 м²/с³; б - А² ® ³ = 38 м²/с³; частота вращения приводного диска: 1 - 100 рад/с; 2-70 рад/с; 2-50 рад/с; 4 - 30 рад/с

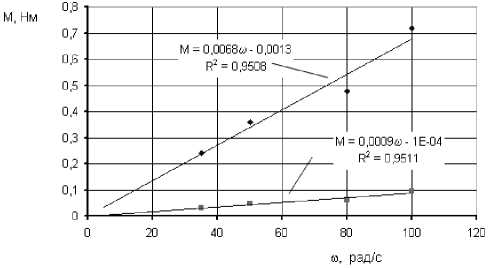
Рис. 3. Изменение момента сопротивления вращению от угловой скорости вращения

т , Па

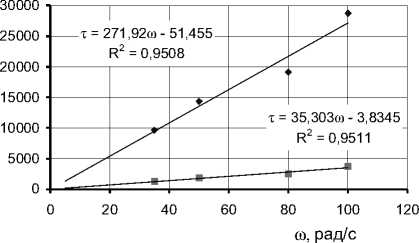
Рис. 4. Изменение касательного напряжения сдвигу от угловой скорости вращения