Определение силовых факторов, развиваемых ортодонтическим аппаратом для расширения верхней челюсти

Одним из факторов успешного лечения аномалий зубочелюстной системы является исследование биомеханического воздействия ортодонтических аппаратов на перемещаемые зубы [4]. Обзор некоторых теоретических и экспериментальных результатов, полученных в этом направлении, представлен, в частности, в монографии [2]. Здесь указано на важность корректного дозирования нагрузки, создаваемой ортодонтическими аппаратами, поскольку превышение развиваемых ими усилий или их некорректное приложение может привести к патологическим процессам, возникающим в периодонте и пародонте при перемещении зубов. Кроме этого, при дозировании нагрузки внимание в основном уделяется нагрузке, действующей со стороны стержня аппарата на корень зуба и направленной вдоль осей координат, поскольку предполагается корпусное перемещение зуба. Поэтому важно корректно выбрать углы наклона стержней аппарата к определенным осям координат, а также точку закрепления стержня на коронке ортодонтического аппарата с тем, чтобы по возможности избежать появления моментов сил, поворачивающих зуб. В настоящей работе представлены результаты анализа сосредоточенных сил и моментов сил, создаваемых ортодонтическим аппаратом с четырьмя стержнями и винтом, применяемым для лечения аномалий верхней челюсти.

Михасев Геннадий Иванович, д.ф.-м.н., проф., завкафедрой био- и наномеханики БГУ, Минск

Минск

Реактивные силы и моменты сил

Верхняя челюсть с установленным ортодонтическим аппаратом представлена на рис. 1. Аппарат развивает усилия, приводящие к перемещению зубов, за счет раскручивания винта, соединяющего пластинки, к которым прикреплены стержни с коронками, жестко закрепленные на зубах. Верхний конец стержня, соединенный с пластинкой ортодонтического аппарата, получает перемещения, равные смещению пластинки аппарата. Далее рассмотрим статическую модель, согласно которой нижний конец стержня соединенный с коронкой, жестко заделан и при перемещении верхнего конца стержня создает в точке закрепления реактивные силы и моменты, под действием которых по истечении определенного промежутка времени начинается перемещение зубов. Такое допущение возможно, поскольку одновременно с раскручиванием винта перемещения зубов не происходит. Расчетная схема для стержня AB ортодонтического аппарата представлена на рис. 2 (точка A соответствует верхнему концу стержня, точка B — нижнему концу стержня).

На рис. 2 точка A , совпадающая с началом координат системы 0 XYZ , в которой верхний конец стержня прикреплен к пластинке ортодонтического аппарата, при раскручивании винта получает перемещение u ₀ , направленное вдоль координатной оси 0 Y . Для определения реактивных силы и момента силы перейдем в координатную плоскость x 0 y , проходящую через ось 0 Y и сам стержень.

Перемещение u_y вдоль оси 0 y найдем из уравнения поперечного изгиба стержня

EI

^д 4 u y д x ⁴

—

R

x

^{д 2} u y д x ²

= 0,

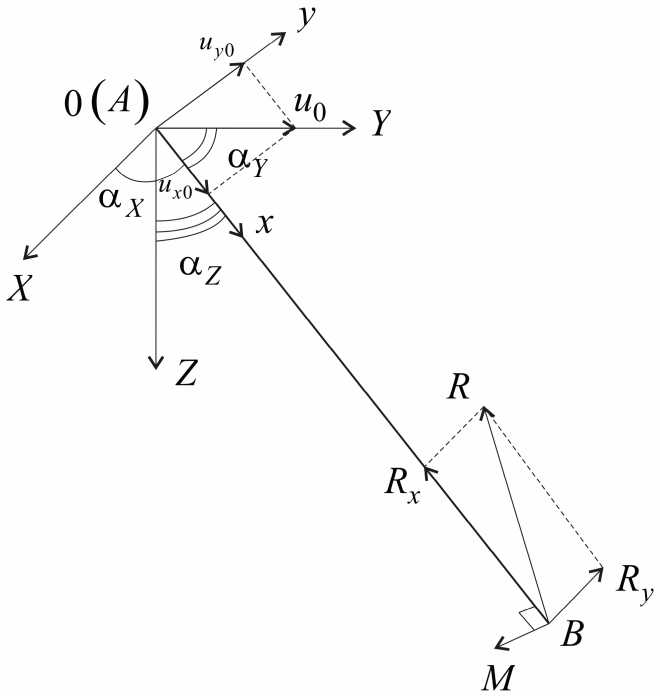
Рис. 2. Расчетная схема для стержня ортодонтического аппарата

С учетом того, что точка B жестко закреплена на зубе пациента, граничные условия представим в следующем виде:

duy (0) duy (l) uy ( 0 ) = u0y, uy (l ) = y = 4    = 0.

л            dx      dx

Здесь u0y = u0sin (aY) - полное перемещение точки A вдоль оси 0y. Из уравнения (1) при граничных условиях (2) получим где

us

Ф =1   о^-

2 Il

u y

u _{0 y}

2 (Ф cos (Ф)- sin (Ф))

( 2Ф ,. х

х -A1-x)cos(Ф) V 1

-

х

Л

У

Из выражения (3) с учетом дифференциальных зависимостей между кривизной оси стержня, сосредоточенной силой и изгибающим моментом будем иметь следующие выражения для реактивных силы и момента сил, возникающих в зубе пациента и действующих в плоскости x 0 y :

Esu 0 x 1 +      ^u 0 x u 0 y s ^cos 2 ^(ф)

l ^   4 Il ( Ф cos ( Ф ) - sin ( Ф ) )

M =

^Eu 0 x^u 0 y s ^sin ( ^Ф ) l ( ф cos ( ф ) - sin ( ф ) )

Для определения усилий, развиваемых ортодонтическим аппаратом в медио-дистальном (касательном к зубному ряду), вестибуло-оральном (перпендикулярном касательной к зубному ряду) и вертикальном направлениях, а также моментов сил, возникающих относительно этих направлений, найдем проекции реакции R на координатные оси системы 0 XYZ и реактивные моменты сил, действующие относительно осей этой системы:

R X ^-

R cos ( a X )

cos2 (a X) + cos2 (aZ) + sin2 (a Y) cot2 (a Y + 81)

R Y - - R cos ( a _Y + 8 1 ) ,

R

Z-

R cos ( a Z )

cos² ( a X ) + cos² ( a Z ) + sin² ( a _Y ) cot² ( a _Y + 8 1 )

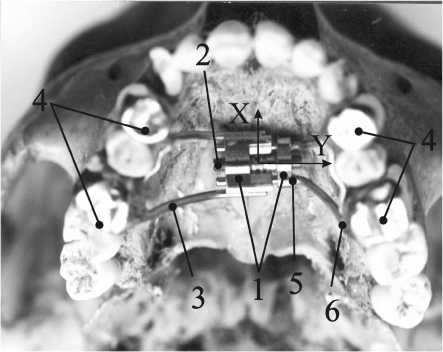
Рис. 1. Верхняя челюсть с установленным ортодонтическим аппаратом: 1 – пластинки; 2 – винт; 3 – стержень; 4 – коронки; 5 , 6 – точки, совпадающие с положением точек А и В на расчетной схеме для стержня ортодонтического аппарата

8 1 - arctan

( Ф U 0 y cos (Ф)    ^V l (Ф cos (Ф)-sin (Ф)) ,,

M cos ( a₇ )                  M cos ( a_K )

M

X

ZX

. / x , MY 0, Mz . , x .

sin (ay)                        sin (aY)

Здесь aX, aY и aZ - углы между стержнем и осями координат 0X, 0 Y и 0Z соответственно. Тогда для реакций Rmd (для медио-дистального направления), Rvo (для вестибуло-орального направления), Rv (для вертикального направления) и моментов сил M md , M vo , Mv , действующих относительно соответствующих направлений, будем иметь

^Rmd ^{- R}X cos ( ⁸ 2 ) ^- R Y sin ( ⁸ 2 ) ^{, R}vo ^{- R}X sin ( ⁸ 2 ) ⁺ R Y cos ( ⁸ 2 ) ^{, R}v ^- R Z ^,

^M md ^- M X cos ( ⁸ 2 ) ^{, M}vo ^- M X sin ( ⁸ 2 ) ^, M v ^- M Z ^, где 8 2 - угол между касательной к зубному ряду и координатной осью 0 X .

Влияние геометрических параметров

Проведем расчет сил и моментов сил, развиваемых ортодонтическим аппаратом при раскручивании винта в медио-дистальном, вестибуло-оральном и вертикальном направлениях. Будем считать, что расстояние, на которое перемещаются пластинки аппарата и 0 - 0,1 мм. Модуль упругости материала, из которого изготовлены стержни, E - 200 ГПа, радиус стержня r - 1 мм, длина стержня l - 2,5 см. На рис. 3 и 4 представлены зависимости реакций, возникающих в медио-дистальном, вестибуло-оральном и вертикальном направлениях при расположении стержня в плоскости Y 0 Z ( a X - 90 ° ) и в плоскости, составляющей угол л/4 с плоскостями X 0 Z и Y 0 Z , от угла a Y и угла a Z соответственно. При построении принимаем угол 8 2 - 30 ° . Значения реакций по оси ординат приведены в кН.

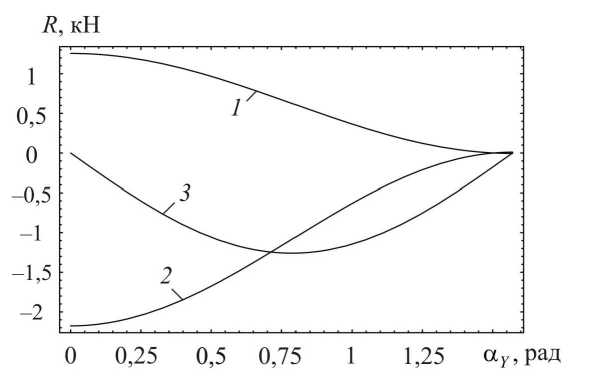
Рис. 3. Зависимости реакций от угла a Y при расположении стержня в плоскости Y 0 Z :

1 -

^^^^^^е

R ; 2 md

R vo

; 3 -

R

v

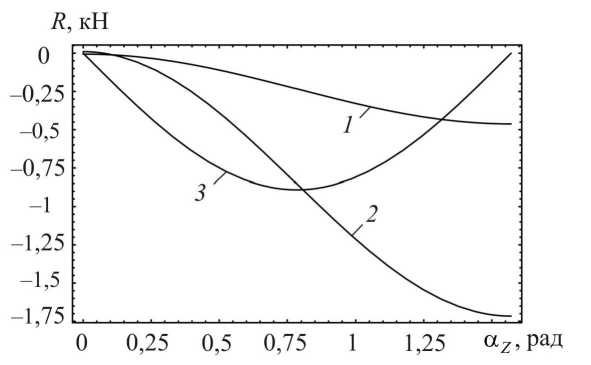
Рис. 4. Зависимости реакций от угла aг при расположении стержня в плоскости, составляющей угол л/ 4 с плоскостями X0Z и Y0 Z : 1 - Rmd ; 2 - Ro ; 3 - Rv

Из рис. 3 видно, что при расположении стержня в плоскости Y 0 Z усилия, развиваемые аппаратом в медио-дистальном и вестибуло-оральном направлениях, максимальны при a _Y = 0, причем R v _o >  R_md . С увеличением угла a Y реакции R_md и R_vo уменьшаются до нулевого значения. Реакция в вертикальном направлении при a _Y = 0 и a _Y = 90 ° равна нулю; максимальное значение реакции R_v наблюдается при a Y = 45 ° .

Как следует из рис. 4, при расположении стержня в плоскости, составляющей угол л/4 с плоскостями X 0 Z и Y 0 Z , с увеличением угла a Z усилия, развиваемые аппаратом в медио-дистальном и вестибуло-оральном направлениях возрастают по абсолютной величине от нуля до максимальных значений. Зависимость реакции R_v от угла a Z аналогична предыдущему случаю.

При увеличении радиуса поперечного сечения стержня усилия, развиваемые ортодонтическим аппаратом по всем направлениям, резко возрастают.

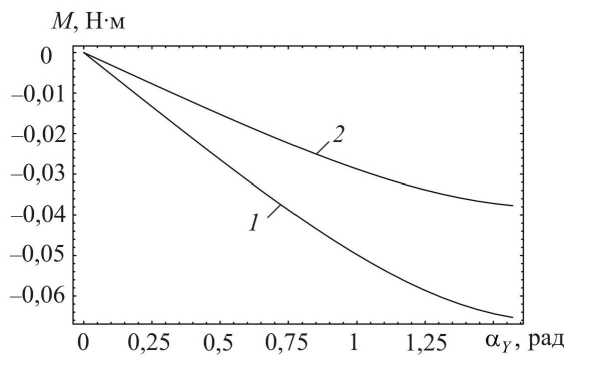
Рис. 5. Зависимости реактивных моментов от угла αY при расположении стержня в плоскости Y0Z : 1 - M ; 2 - M md vo

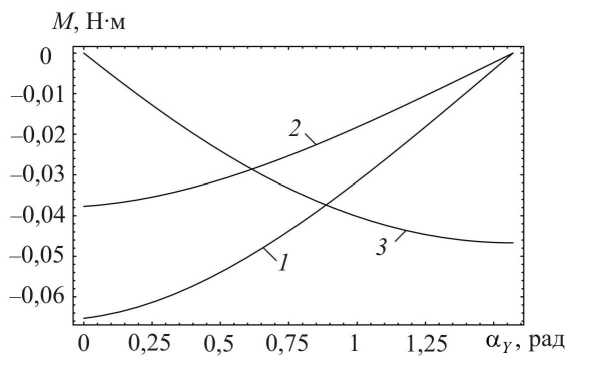
Рис. 6. Зависимости реактивных моментов от угла α _Z при расположении стержня в плоскости, составляющей угол π/4 с плоскостями X 0 Z и Y 0 Z : 1 - M_md ; 2 - M_vo ;

3 - M

v

Визуализация зависимостей для реактивных моментов сил, возникающих относительно медио-дистального и вестибуло-орального направлений, а также относительно оси 0 Z , в двух рассматриваемых плоскостях выполнена на рис. 5 и 6 (значения моментов сил по оси ординат приведены в Н ⋅ м). При построении приняты прежние числовые данные.

Из рис. 5 видно, что при расположении стержня в плоскости Y 0 Z при α _Y = 0 все реактивные моменты равны нулю. С увеличением α _Y моменты сил M_md и M_vo возрастают по абсолютной величине. Момент сил M_v равен нулю. В случае, если стержень располагается в плоскости, составляющей угол π/4 с плоскостями X 0 Z и Y 0 Z , отличными от нуля являются все три реактивных момента.

Анализ аналогичных зависимостей, построенных для различных радиусов поперечного сечения, показывает, что с увеличением r реактивные моменты возрастают и убывают соответственно.

Конечно-элементный анализ реакций и реактивных моментов

Выполним конечно-элементный расчет реакций и реактивных моментов, возникающих в точке закрепления стержня на коронке аппарата, с применением функциональных возможностей пакета ANSYS . Геометрическая модель ортодонтического аппарата, построенная в CAD -пакете CATIA V 5 для случая, если углы наклона стержней к координатным осям равны между собой, длина стержня составляет 25 мм, радиус стержня равен 1 мм, представлена на рис. 7.

Один из концов стержня закреплен на насадке аппарата, которая надевается на зуб. Другой конец каждого из стержней закреплен на одной из граней двух пластинок, которые моделировались в форме параллелепипедов. Далее рассмотрим один из стержней модели ортодонтического аппарата, считая корень зуба жестко заделанным в костной ткани в момент раскручивания винта ортодонтического аппарата. Конец стержня, закрепленный на пластинке, получает перемещение, равное 0,1 мм, в направлении оси абсцисс. Расчетная модель с визуализацией положения стержня до и после перемещения одного из его концов показана на рис. 8. Упругие свойства стержня описываются константами E = 200 ГПа, v = 0,3; радиус поперечного сечения стержня равен 1 мм, длина стержня составляет 25 мм.

В ходе проведения вычислительного эксперимента стержень моделировался линейными пространственными балочными конечными элементами Beam 188 и Beam 4. Элемент Beam 188 построен на основе балки Тимошенко, имеет шесть степеней свободы и пригоден для линейных, а также нелинейных задач с большими поворотами и деформациями. В качестве входных данных элемента используются геометрические параметры его поперечного сечения. Балочный конечный элемент Beam 4 является элементом с одной осью и имеет возможность воспринимать растяжение, сжатие кручение и изгиб. Так же как и элемент Beam 188, Beam 4 имеет шесть степеней свободы в каждом узле. Элемент определяется двумя узлами, площадью поперечного сечения, двумя моментами инерции и двумя толщинами [1]. В нашем случае использовался балочный конечный элемент Beam 4.

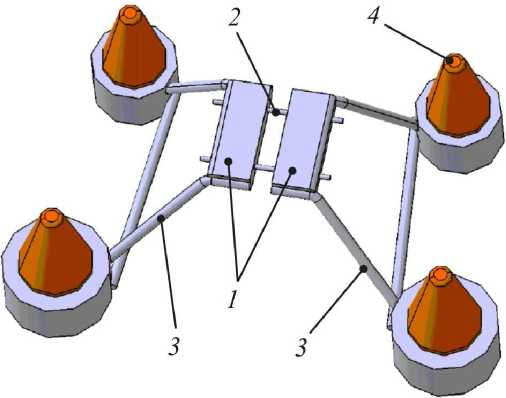
Рис. 7. Геометрическая модель ортодонтического аппарата: 1 – пластинки; 2 – винт;

3 – стержень; 4 – зуб

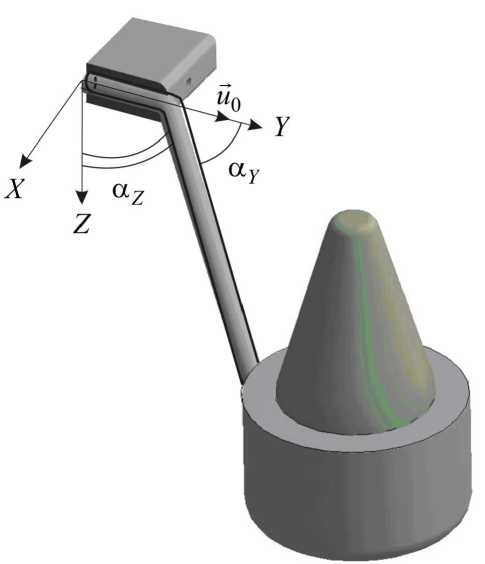
Рис. 8. Положение стержня ортодонтического аппарата до и после перемещения пластинки

В результате конечно-элементного расчета получены значения реакций и реактивных моментов, возникающих в точке закрепления стержня аппарата на коронке, для различных углов наклона стержня по отношению к осям декартовой системы координат. На рис. 9 и 10 выполнена одновременная визуализация значений реакций, найденных в пакете ANSYS для определенных углов наклона стержня α _Y и α _Z в плоскости Y 0 Z и в плоскости, составляющей угол π /4 с плоскостями X 0 Z и Y 0 Z (обозначены точками), и зависимости (6) от угла α _Y и α _Z в тех же плоскостях. При построении зависимостей (6) для стержня принимались числовые данные, используемые при конечно-элементном расчете.

Из рис. 9 и 10 видно, что результаты конечно-элементного расчета и вычисления реакций на основании решения уравнения (4) практически совпадают. Расхождения в некоторых случаях наблюдаются при предельных углах наклона стержня аппарата к осям координат, равных нулю и π /2. Значения реакций в этих случаях могут отличаться в 4–7 раз. Для остальных углов наклона стержня отличие результатов конечно-элементного расчета при использовании элемента Beam 4 по сравнению с вычислением реакций на основании аналитических выражений не превышало 0,5 % . Также отметим, что при проведении аналогичных расчетов с применением балочного элемента Beam 188 расхождение результатов не превышало 1,5 % . В связи с этим можно сделать вывод о том, что для получения более корректных результатов целесообразнее использовать балочный конечный элемент Beam 4.

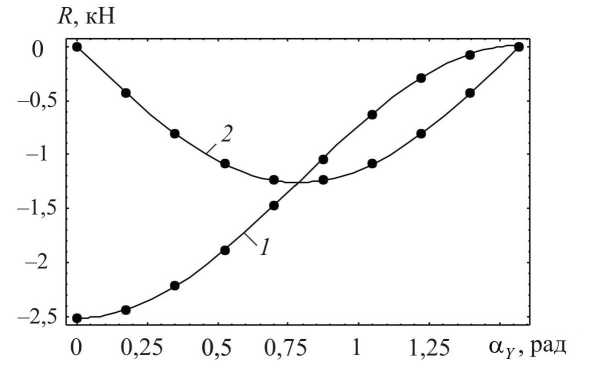
Рис. 9. Зависимости реакций от угла α _Y при расположении стержня в плоскости Y 0 Z (сплошные линии) и значения реакций, полученные в ходе конечно-элементного расчета (обозначены точками): 1 - R_y ; 2 - R z

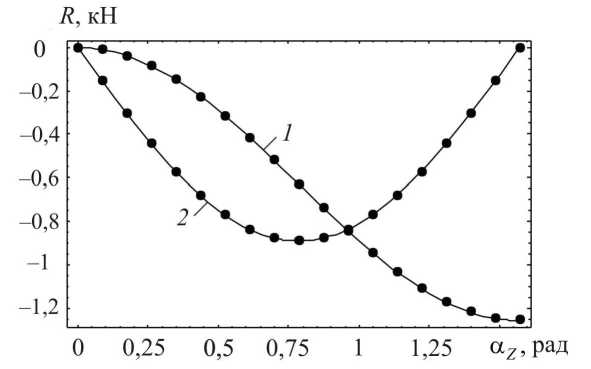
Рис. 10. Зависимости реактивных моментов от угла α _Z при расположении стержня в плоскости, составляющей угол π/4 с плоскостями X 0 Z и Y 0 Z (сплошные линии), и значения реакций, полученные в ходе конечно-элементного расчета (обозначены точками): 1 - R_x = R_y ; 2 - R z

Значения реактивных моментов для определенных углов наклона стержня α _Y и α _Z в плоскости Y 0 Z и в плоскости, составляющей угол π /4 с плоскостями X 0 Z и Y 0 Z , и зависимости (7) от угла α _Y и α _Z в тех же плоскостях приведены на рис. 11 и 12. При построении зависимостей (7) для стержня используются те же числовые данные, что и при конечно-элементном расчете.

Максимальное отличие результатов конечно-элементного расчета реактивных моментов по сравнению со значениями, найденными в соответствии с выражениями (7), составляет в первом случае 9,8%, во втором - 12,5%. Приемлемая величина погрешности конечно-элементного расчета указывает на пригодность использования

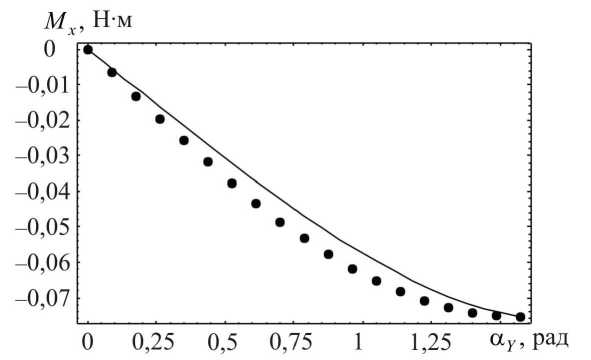
Рис. 11. Зависимость реактивного момента M x от угла α _Y при расположении стержня в плоскости Y 0 Z (сплошная линия) и значения реактивного момента, полученные в ходе конечно-элементного расчета (обозначены точками)

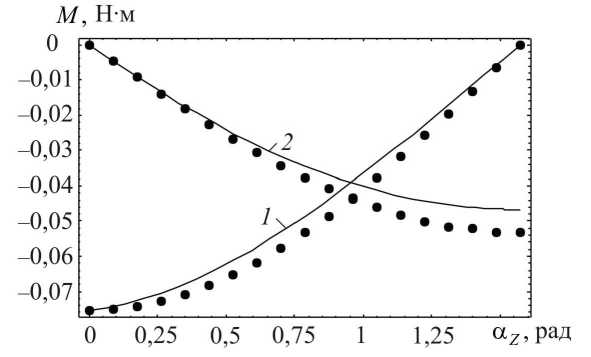
Рис. 12. Зависимости реактивных моментов от угла αZ при расположении стержня в плоскости, составляющей угол π/4 с плоскостями X0Z и Y0Z (сплошные линии), и значения реакций, полученные в ходе конечно-элементного расчета (обозначены точками): 1 - M , 2 - M xz предложенной методики вычисления усилий, возникающих в стержнях аппарата при ортодонтическом лечении, и для других типов моделей и граничных условий.

Заключение

• 1.    Полученные в работе результаты численных расчетов силовых факторов, действующих на зуб при перемещении пластинок ортодонтического аппарата, показывают, что значения наибольших реактивных моментов сил значительно меньше максимальных моментов, создаваемых силами давления. Поэтому можно сделать вывод о том, что повороты зубов в ходе ортодонтического лечения рассматриваемым аппаратом обусловлены не конструкцией самого аппарата, а теми моментами, которые создают силы давления. Эти моменты сил будут принимать тем большие значения, чем больше расстояние от точки закрепления стержня на коронке до соответствующего центра сопротивления зуба.

• 2.    Также следует отметить, что не следует пренебрегать моментами сил, действующих на зуб со стороны стержня ортодонтического аппарата, поскольку из-за малой жесткости периодонта при поворотах корня [5] действие даже незначительных моментов сил может привести к появлению достаточно высоких углов поворота зуба относительно первоначального положения. Это тем более следует при атрофии костной ткани, приводящей к существенному снижению жесткостей периодонта [3].

• 3.    Также отметим, что приемлемое совпадение результатов конечноэлементного расчета реакций и результатов, полученных на основании соотношений (6), (7), показывает, что полученные формулы для нахождения усилий, развиваемых ортодонтическим аппаратом для расширения верхней челюсти, могут быть непосредственно использованы на практике стоматологами-ортодонтами для корректного прогнозирования нагрузки, приходящейся на перемещаемые зубы.

Из практики ортодонтов следует, что усилия, развиваемые ортодонтическим аппаратом при активации винта аппарата, меньше значений, полученных в ходе аналитического и конечно-элементного расчета. Это обстоятельство можно объяснить распределением реальной нагрузки по поверхности коронки, а также наличием периодонтальной связки, снижающей нагрузку на костную ткань. Возможные погрешности в определении реактивных сил и моментов обусловлены постановкой задачи, принятой в настоящей статье, при которой рассматривается действие сосредоточенной нагрузки на жестко заделанный корень зуба.

Благодарности

Работа выполнена при поддержке Государственного комитета по науке и технологиям Республики Беларусь    (проект «Разработать методику автоматизированного проектирования и оптимизации конструкций зубочелюстных протезов и ортодонтических аппаратов при аномалиях и деформациях челюстнолицевой области, обусловленных расщелинами губы и неба, с применением универсальных CAD/CAE/CAM-систем»).