Определение собственных частот простейшей механической системы на упругом основании

Расcматриваемая простейшая механическая система лежит в основе виброзащитной системы, в которой твердое тело представляет собой защищаемое тело, пружина-амортизатор, упругий стержень-основание. Особенность математической модели, описывающей движение механической системы, в том, что в ней учитываются не только упругие свойства основания, но и конечность массы основания. В ранних работах авторов была предложена методика получения уравнений на собственные частоты. В статье по данной методике собственные частоты выделяются сначала графически, а затем рассчитываются с использованием пакета MathCAD.

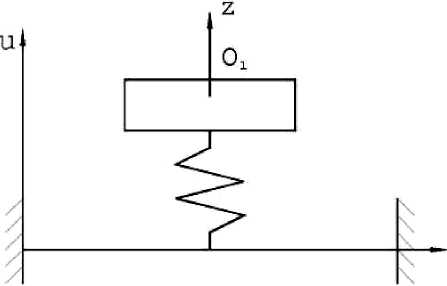
Рассмотрим механическую систему на упругом основании (рис. 1) – твердое тело, присоединенное к упругому стержню с помощью пружины. Концы стержня закреплены шарнирно.

Твердое тело имеет массу M , пружина – жесткость с , упругий стержень – длину l . Механическая система закреплена на стержне в точке x = a , z – координата твёрдого тела, принимаемого за материальную точку в положении статического равновесия, u – поперечное смещение стержня, р - плотность материала стержня, F - площадь поперечного сечения стержня, J – момент инерции поперечного сечения стержня относительно нейтральной оси сечения, перпендикулярной плоскости колебаний.

0           а             1

Рис. 1.

Движение указанной системы описывается гибридной системой дифференциальных уравнений:

„ d ² z    ,     ,

M —T + c(z - u(a, t)) = 0, dt d2u   ,.,d4u     , z ez pF —— + EJ —— = c(z - u(x, t))£(x - a).

I    d t        dx

c        EI c

Обозначим: — = p , --- = b , --- = e . Поделив обе части первого уравнения на m , а

M    pF   pF второго на pF, получим систему:

z + p ²( z - u ( a , t )) = 0,

где p =

д u   Э u

—у ⁺ b — = e ⁽ z ^{- u} ( ^x , t ⁾⁾ d ^{( x -} a ), d t      d t

EJ      c

, b = ---, e =--- . На u ( x,t ) наложены граничные условия:

pF    pF

—u (0, t) = -U (l, t) = 0, u (0, t) = u (l, t) = 0, dx        дx решение системы (2) ищем в виде z (t) = A sin( tot + y), u (x, t) = V (x) sin( tot + y) в результате получим:

-to" A + p ²( A - V ( a )) = 0, - to" V ( x ) + b d V⁽x ) = e ( A - ( x )) ^ ( x - a ) .         (5)

dx ⁴

Здесь А и V(x) , соответственно, неизвестная величина и функция. Отметим, что второе соотношение из (5) понимается в обобщенном смысле, т.е. для любой функции ф ( x , t ) из

некоторого класса справедливо:

( -to V ( x ) + b д ( x ) ) ф ( x , t ) dx = e ( A - V ( x )) ф ( a , t ).

.

Из граничных условий (3) получим условия, накладываемые на функцию V(x):

dVdV

— (0) = -- (l) = 0, V(0) = V(l) = 0. dxdx

В [1] показано, что при любых to и А функция v (x)=V(x -a)Ae

1 + eV (0)

удовлетворяет соотношению (6) . Здесь V ( x ) является решением уравнения

T V ( x ) + b

d^l = * x ) . dx

С краевыми условиями

V ( - a ) = 0, V ( a ) = 0_:

д ² V , . a d ² V . . .

1, -. 2 (-a) = 0,      2 (a) = 0- дx           дx

Отметим, что из (8) следует:

V ( a ) = V-A .

1 + eV (0)

Краевая задача (9) – (10) решается путем представления V(x) в виде суммы обобщенного решения G0 (x) однородного уравнения d 4V (x)

-mV (x)+ь —4-^ = 0

dx ⁴

и обобщенного решения G ( x ) неоднородного уравнения (12), то есть

V ( x ) = G ₀ ( x ) + G ( x ),

где

G ₀ ( x ) = c 1 S 1 ( P x ) + c 2 S 2 ( в x ) + c₃ S 3 ( в x ) + c 4 S ₄ ( в x ),

S№ ) =

cosh( в x ) + cos( в x )

S з ( в х ) =

cosh( в x ) - cos( в x )

, S 2 ( в х ) =

sinh( в x ) + sin( e x )

, S 4 ( в х ) =

sinh( в x ) - sin( в x )

,

– функции Крылова, с 1 , с 2 , с 3 , с 4 – неизвестные постоянные [2]. Постоянные с 1 , с 2 , с 3 , с 4 находятся из краевых условий. Частное решение G ( x ) можно представить в виде

G ( x ) = S ( x ) S в ¹ >

где ^ ( x ) - функция Хэвисайда [3], в = — т

.

b ⁴

Опишем процедуру определения собственных частот. Из первого уравнения системы (5) 22

V ( a ) = PL ZT a .

p ²

Приравнивая правые части полученного выражения и (11) и сокращения на А, получаем уравнение для собственных частот системы:

-т2 + —p=— = 0, 1 + eV (0)

где V(0) = c1 можно найти из граничных условий (10), решив систему линейных алгебраических уравнений относительно с1, с2, с3, с4 вида c1 S1 - c2 S2 + c3 S3 - c4S4 = 0, c1 S1 + c 2 S2 + c3 S3 + c4 S4 = - a 0 S4,

c1 S3 - c2S4 + c3S1 - c4S2 = 0, c1 S3 + c 2 S4 + c 3 S1 + c4 S2 = - a 0 S2, для которой

∆

∆1 =

-j

-j

S 1	- S 2	S 3	- S 4
S 1	S 2	S 3	S 4
S 3	- S 4	S 1	- S 2
S 3	S 4	S 1	S 2
0	- S 2	S 3	- S
a 0 S 4	S 2	S 3	S 4
0	- S 4	S 1	- S
a 0 S 2	S 4	S 1	S 2

= 4( S 2 ² - S 4 ²)( S 1 ² - S 3 ²),

= 2 a ₀( S ₄ ² - S ₂²)( S ₁ S ₄ - S ₂ S ₃) .

∆

Далее c = ¹ . Подставляя в (14), после преобразований получаем 1 _∆

16 λ ³ ( S 1 ² - S 3 ² ) = χ ( S 2 S 3 - S 1 S 4 ).

Учитывая, что   S ₁ = S ₁ ( λ ), S ₂ = S ₂ ( λ ), S ₃ = S ₃ ( λ ), S ₄ = S ₄ ( λ ) , где λ = β a , a = 2 ,

получим частотное уравнение

32 λ ³ ch λ cos λ = χ ( ch λ sin λ - sh λ cos λ ) .

Разделив обе части на ch λ cos λ , получим

32 λ ³ = ( tg λ - th λ ) χ ,

λ=

1 ,

16 λ ⁴ b

Из (19) имеем ω ² = l ₄

pl ²

Обозначив λ =

04V b

2 b ⁴

₌    cl ³ ω ²

^{χ =} EJ ( p ² - ω ²)

.

. Подставляя все в (20), получим:

cl ³ λ ⁴

χ =      _{2 4}

EJ ( ^{p l} - λ ⁴)

16 b

.

cl ³                   b λ ⁴

, b ₀ = c , получим χ = ⁰     . Подставим в (18) и преобра-

⁰ EJ                 λ ₀ ⁴ - λ ⁴

зовав, получим более простое для анализа и нахождения решения частотное уравнение:

32( λ ⁴ - λ ⁴ )

⁰       = tg λ - th λ .

b0λ

Определим собственные частоты, решая уравнение (22) в среде MathCAD при следующих параметрах механической системы:

l = 1, M = 10, c = 10000, F = 0,0025, E = 1, J = 1, ρ = 8000

Графики двух функций в (22) имеют вид (рис. 2).

В точках пересечения двух графиков (рис. 2) находим значения параметра λ , а затем

пересчитываем их в собственные частоты по формуле ω =   l ₂

.

В результате получаем дискретный набор из первых пятнадцати собственных частот нашей механической системы (таблица 1).

На самом деле набор собственных частот бесконечный, что объясняется присутствием в частотном уравнении периодических тригонометрических функций, а с физической точки зрения непрерывным распределением конечной массы стержня по его длине.

Заметим, что начиная с седьмой гармоники расчет частот можно производить по приближенной формуле где 1k = 16 + (k - 6)n, k = 7,8,

4 1 2 to = k k l 2

..., n ,... ,

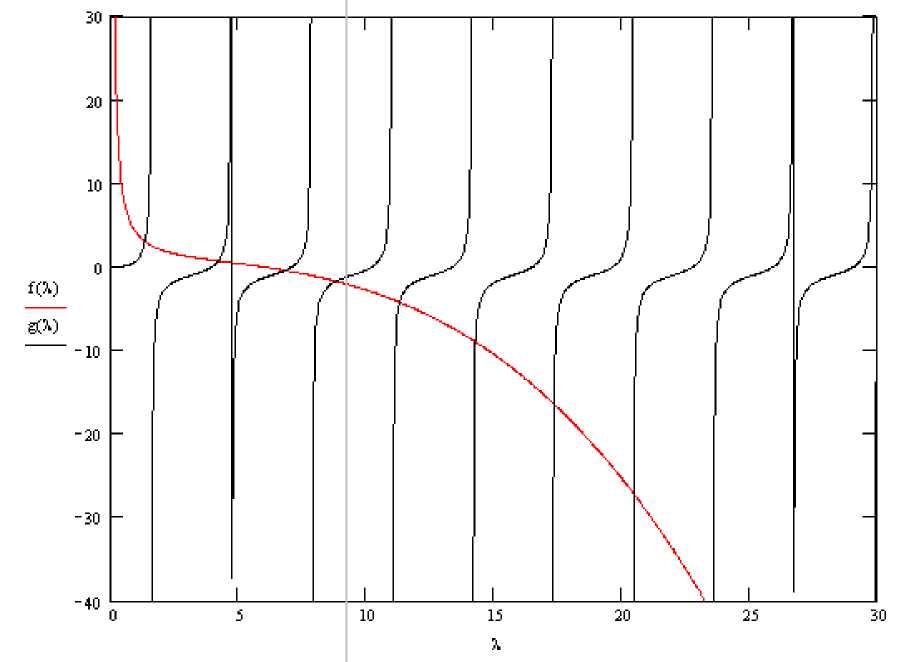
Рис. 2

Таблица 1

№ п\п	Параметр 1 (безразмерный)	Частота to (1/сек)
1	1,319	1,556
2	4,186	15,673
3	6,807	41,444
4	8,798	69,233
5	11,294	114,088
6	14,261	181,905
7	17,343	269,025
8	20,458	374,344
9	23,586	497,569
10	26,720	638,584
11	29,857	797,329
12	32,996	973,795
13	36,135	1168
14	39,275	1380
15	42,416	1609

Заключение

На основе методики, предложенной авторами, рассчитаны собственные частоты механической системы на упругом стержне с закрепленными краями и установленным на нем твердым телом, присоединенным к упругому стержню с помощью пружины, моделирующей виброзащитную систему. Специфика расчета заключается в таком расщеплении частотного уравнения на две части, чтобы можно было отделить точки пересечения графиков функций, задающих эти части, а затем определить частоты с помощью программы, встроенной в пакет MathCAD. Определены первые пятнадцать собственных частот. Следует заметить, что начиная с седьмой гармоники расчет частот можно приближенно производить аналитически.