Определение собственных колебаний кусочно-однородных вязкоупругих тел с использованием пакета ANSYS

инженерного анализа. В большинстве подобных систем для численной реализации задач МДТТ используется метод конечных элементов (МКЭ). Примерами стандартных систем инженерного анализа (САЕ-системы) являются ANSYS, LS-DYNA, ADINA, ABAQUS, COSMOS. Основными отличительными особенностями, обеспечившими востребованность таких пакетов программ, являются: широкий спектр решаемых задач; удобные для пользователя процедуры задания информации о геометрии, граничных условиях и других параметрах моделируемого объекта; широкие возможности представления результатов.

Известные системы инженерного анализа постоянно развиваются и пополняются новыми задачами. Однако имеется ряд задач МДТТ, которые пока не входят в САЕ-системы, и для того, чтобы они были включены туда, требуется определенное время.

В связи с этим при постановке новых и важных для практических приложений задач имеют место два подхода. Первый из них, наряду с постановкой новой задачи и написанием алгоритма её численной реализации, содержит разработку программы для пользователей. Этот путь малоэффективен, если иметь представление о том, какие усилия и средства затрачиваются на создание востребованных САЕ-систем. Второй подход связан с максимальным использованием известных САЕ-систем для решения новых механических задач. В данной работе используется второй подход, то есть рассматриваются варианты использования известного пакета программ, а именно пакета ANSYS, для решения задачи собственных колебаний кусочно-однородных вязкоупругих тел [1, 2].

Оптимизация диссипативных свойств объектов, состоящих из элементов, механическое поведение которых описывается моделью линейного упругого тела или моделью наследственной теории вязкоупругости, достаточно эффективно осуществляется на основе решения задачи собственных колебаний. В известных САЕ-системах данная механическая задача отсутствует.

Приведем математическую постановку задачи собственных колебаний кусочно-однородных вязкоупругих тел. Тело объема V состоит из N однородных упругих или вязкоупругих частей, имеющих объемы V_k ( k = 1, 2, …, N ) и ограничено поверхностью S = S u + S _o . На части поверхности S u заданы нулевые кинематические, а на части поверхности S _о — нулевые силовые граничные условия. На поверхности контакта частей составного тела выполняются условия идеального скрепления. Деформации с перемещениями связаны линейными соотношениями Коши. Для упругих частей механическое поведение материала описывается соотношениями линейной теории упругости:

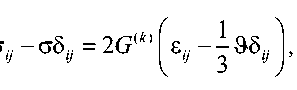
ст..-ст5. = 2 G ^{( k} ) [е..- ¹ 95.. ij ij                     i ij з ij

o = B ^{( k} ) 9 ,

а для вязкоупругих частей — соотношениями линейной теории вязкоупругости:

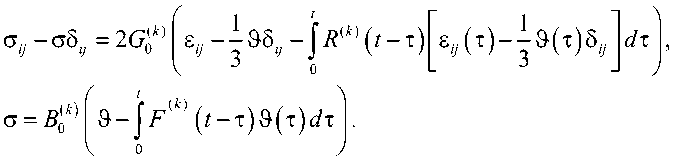
° и-°⁵_ц = ² G 0 k )

CT

B 0 ^k ) 9- j F ( k ) ( t -t ) 9 ( t ) d т

Здесь G ^{( k )} , B ^{( k )} — упругие сдвиговые и объемные модули; G ₀ ^{( k )} , B ₀ ^{( k )} — мгновенные сдвиговые и объемные модули; R ⁽ k ) , F ⁽ k ) — ядра релаксации; G = G jj /3 — среднее напряжение; 9 — объемная деформация.

В поставленной задаче необходимо найти решение вида

Ui( x, t ) = e-i" 5, (x),

удовлетворяющее принципу возможных перемещений

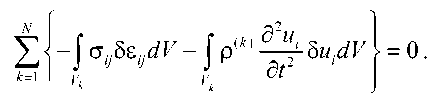
■⁽ k ) ^^ 5 udV d t ^{-     1}

E ^- J ^c j ⁵⁸ udV ^- J p¹

k = 1

Здесь го = го _R + i го I — комплексная собственная частота колебаний; го _R — резонансная частота; го I — показатель демпфирования, характеризующий скорость затухания колебаний; £ _i — компоненты вектора собственных форм колебаний; p ^{( k} ) — плотность материала.

Если далее предположить, что начальные возмущения не влияют на поведение системы в текущий момент времени и изменения амплитуд затухающих колебаний во времени малы, то можно заменить физические соотношения (2) их комплексными аналогами (подробно эта процедура обсуждается в работе [3]):

0,-^5,, = -G(k) (slV-95z/),          о = В(k) 9.

ijij      ijij

Входящие сюда G ^{( k} ) = G R^k ) + iG ,^k ) , В ^{( k} ) = B R^k ) + iB |^k ) — комплексные сдвиговой и объемный модули, для которых справедливы соотношения:

G Rk ’ = G 0 * ’ I - R k ' ( " R ) ] ,

G “' = G 0 * - R <* - ( _Ю r ),

В »'> = В 0 k ’ F Sk ’ ( to r ),

BR“= B0 »[1 - F> R)], да

R⁽c k ) ( " r ) = J R ( k ) ( ^T ) cos " r т d t ,

да

R S^k ’( " r ) = J R ^{( k} ) ( t ) sin "  r т d т ,

да

F C^k ) ( ro _R ) = J F ^{( k} ) ( т ) cos ro _R т d t ,

да

F ( ^k ) ( ro _R ) = J F ^{( k} ) ( т ) sin ro _R т d т .

Для численной реализации используем метод конечных элементов [4], который приводит задачу собственных колебаний кусочно-однородного тела к алгебраической проблеме комплексных собственных значений:

{[ K ]-"- [ M ]}{6}= 0,

где [ K ] , [ M ] — соответственно матрица жесткости и матрица масс кусочно-однородного тела.

Рассмотрим первый вариант численной реализации поставленной задачи средствами пакета ANSYS. Программный комплекс ANSYS позволяет строить разнообразные конечно-элементные сетки сложных неоднородных пространственных тел, которые могут импортироваться из ANSYS в виде текстовых файлов. В рамках упругой задачи могут быть получены глобальные матрицы жесткости и масс, доступные в формате хранения конечно-элементных матриц Harwell–Boeing.

Для того чтобы при решении задачи собственных колебаний вязкоупругого тела можно было использовать матрицу жесткости, полученную для соответствующего упругого тела, последнюю необходимо представить в виде компонентов K_b и K_g , пропорциональных объемному и сдвиговому модулям:

[K ] = B [ Kb ] + G [Kg ] . (7)

Такая структура матрицы жесткости позволяет осуществить переход к используемой модели вязкоупругого тела (5) путем замены G и B на соответствующие вязкоупругие выражения.

Однако программный комплекс ANSYS не позволяет представить глобальную матрицу жесткости в виде компонентов, пропорциональных объемному и сдвиговому модулям. Для изотропного тела могут быть заданы только технические константы: модуль упругости E и коэффициент Пуассона v . Поэтому для решения задач колебаний неоднородных вязкоупругих тел с использованием перечисленных возможностей пакета ANSYS был разработан специальный алгоритм, а также написаны макросы на APDL (ANSYS Parametric Design Language) [5] и программы на языке FORTRAN.

Основную идею предлагаемого алгоритма рассмотрим на примере однородного вязкоупругого тела. Программный комплекс ANSYS формирует глобальную матрицу жесткости для изотропного материала с использованием технических констант E , v . Для получения матриц [ K_b ] , [ K g ] , входящих в (7), выполним в ANSYS два построения матриц жесткости с различными значениями констант E , v . Получим систему двух уравнений:

[ K ]i = a [ Kb ] + bi [ Kg ] ■ [K ]2 = a2 [Kb ] + b, [ Kg ].

Здесь:  a, = . E1 . ,  a2 = . E2 . , b = , E1 _  b2 = , E2 . ;  [K]  и [K1 —

1   3 (1 - 2v1)     2 3 (1 - 2v2)     1 2 (1 + v1)     2 2 (1 + v2)    L J1 L h матрицы жесткости, полученные в ANSYS при значениях механических констант E1, v1 и E2, v2.

Решение системы (8) имеет вид:

1- ^b 1 ^{[ K ]}2 - ^b 2 ^{[ K ]}1          V_K a-K 2 ^{[ K ]}2 - a 1 ^{[ K ]}1

[ Kb] nh-nh ,     [ Kg ]    nh-nh a 2 b1 a1 b 2                            a 2 b1 a1 b2

Рассмотрим в качестве примера одну из возможных комбинаций значений констант в решении (9):

E 1 = 1; v 1 = 0;

^a 1    3;     ^b 1    2; ^E 2    3

v2 =-

a, = —;   b = —

.

Тогда [ K b ] = [ К ] 2 - [ K ] , , [ K g ] = I ( 4 [ К ] , - [ К ] 2 ) .

Таким образом, средствами пакета ANSYS получен следующий конечно-элементный аналог задачи собственных колебаний составного вязкоупругого тела:

( B [ K b ] + G [ K g ]-_Ю’ [ M ] ) { и } = 0.                                               (10)

Для решения образовавшейся алгебраической проблемы комплексных собственных значений может быть использован любой подходящий алгоритм, в частности, алгоритм на основе метода Мюллера [6].

В случае кусочно-однородного вязкоупругого тела матрица жесткости имеет следующую структуру:

[ K ] = £ ( G k [ K g ]'“+ B k [ K, ]* k) ) •                                                   (11)

k =1 ^x                                         '

где [ K_g ]^{( k )} и [ K_b ] ^{( k )} — соответствующие матрицы для k -й подобласти, при вычислении которых используются вышеприведенные значения E 1 , v 1 и E ₂, v ₂. В других подобластях значения модулей E ₁ и E ₂ задаются на несколько порядков меньше; в частности, в выполненных численных экспериментах принято E 1 = E ₂ = 10 ^{- 5} . Значения v 1 , v ₂ в подобластях, отличных от k , формально могут быть достаточно произвольными. В реальных расчетах коэффициенты Пуассона были нулевыми.

Второй вариант использования пакета ANSYS для решения задачи собственных колебаний кусочно-однородных вязкоупругих тел основан на идее представления искомого решения в виде линейной комбинации векторов собственных форм колебаний соответствующего упругого тела (метод главных координат) [7]:

{ 8 } »[ { ^ } . { ^ } 2- { ^ } > -{ ^ } m ]' { Р 1 , Р 2 ,-, P m } ^T = [ ^У Ж ■                          (¹²)

Здесь { ^ } 1 { ^ } 2 ... { ^ }. ... { £ } m — векторы собственных форм колебаний; { p 1 , p 2 ,..., p_m } — вектор коэффициентов линейной комбинации.

Подставляя (12) в (6), для нахождения ю получим алгебраическую задачу на комплексные собственные значения размерности m х m :

det ([^ ]T ([ K ]-ю2 [М ])[^ ]) = 0.

Здесь матрица жесткости [ K ] , имеющая вид (11), и матрица [ М ] определяются с помощью программного комплекса ANSYS согласно ранее изложенной процедуре. Собственные векторы { и }. упругого тела находятся из модального анализа в пакете ANSYS. Для решения поставленной в работе задачи разработан алгоритм и написаны макросы на APDL и программа на языке FORTRAN.

В рассматриваемой задаче собственных колебаний основная трудность вычислений связана с решением алгебраической проблемы комплексных собственных значений. Использование метода главных координат позволяет существенно снизить порядок разрешающей системы алгебраических уравнений. Поэтому подход на основе метода главных координат имеет положительные перспективы при решении других динамических и нелинейных задач механики деформируемого твердого тела. Во всех случаях для решения возникающей алгебраической проблемы комплексных собственных значений используется алгоритм, основанный на применении метода парабол (метода Мюллера).

Приложения задачи собственных колебаний вязкоупругих тел, главным образом, связаны с оптимизацией диссипативных свойств конструкций. Для иллюстрации решена задача определения демпфирующих свойств двухслойного цилиндра, находящегося в двух жестких опорах, прочно скрепленных с ним (подобная задача возникает, например, при транспортировке). Внутренний слой цилиндра был выполнен из вязкоупругого материала, а внешний — из упругого материала. Рассматривались два способа крепления: с полным (Рис. 1, а ) и частичным (Рис. 1, б ) охватом цилиндра по окружности. Опоры располагались симметрично, их положение определялось величиной Z ₀ .

В качестве оптимизационного критерия при анализе демпфирующих свойств использовалось следующее соотношение [2]:

го ⁰ ( Ф I ) = max min [ю i ( Ф I ) ] . (14)

Здесь го ⁰ ( Ф I ) — оптимальная величина показателя демпфирования го I (см. выражение (4)); Ф I ( Ф 1 , Ф ₂ ,..., Ф t ) — оптимизируемые параметры (в рассматриваемой задаче оптимизируемый параметр один — Z ₀ ); N — количество анализируемых собственных частот колебаний ( i = 1, 2,..., N ).

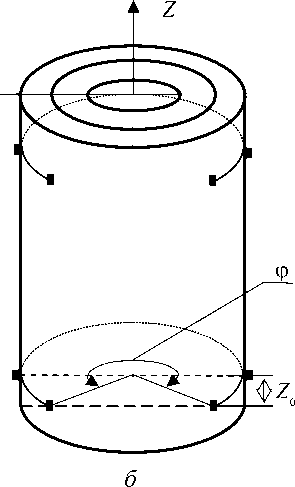
Рис. 1. Расчетные схемы задач

Для проведения вычислений были выбраны следующие значения параметров задачи: L / R = 4; R 1 / R =0,3; R ₂/ R =1,01; R ^ = 0; R^ = 0,2; F^¹ = F^ = 0; B 01) / G 01) = 24,7 ; G ⁽²⁾ / G ₀ ⁽¹⁾ = 10 ² ; B ⁽²⁾ / G 01) = 217,0; p ⁽²⁾ / p ⁽¹⁾ = 1, а также предполагалось, что материал наполнителя при объемном деформировании ведет себя упругим образом. При решении задачи применялись оба вышеприведенных варианта использования пакета ANSYS. При этом конечные элементы имели вид тетраэдра с линейной аппроксимацией полей перемещений. Число узлов в расчетах составляло ~ 4 • 10 ³ .

Пример 1. Исследовался цилиндр с кольцевыми опорами (Рис. 1, а ). В таблице (в числителе) для первых трех комплексных собственных частот колебаний приведены безразмерные действительные части ( ro R = ro _R • R J р ⁽¹⁾ / G 01) ) и соответствующие им мнимые части ( ro * = ro I • R р ⁽¹⁾ / G 01) ). Численные эксперименты показали, что удержание в решении (12) 3, 10 и 20 собственных форм колебаний приводит к отличию результатов в пределах 1%.

Таблица (в знаменателе) также содержит значения трех собственных частот, полученные при непосредственном использовании метода конечных элементов [8]. При этом использовалось представление решения в виде ряда Фурье по окружной координате и кольцевые треугольные элементы с линейной аппроксимацией полей

Таблица. Сравнение результатов расчета первых трех собственных частот колебаний цилиндрического тела при использовании пакета ANSYS и традиционной схемы МКЭ

Z 0* * roR * ГО I 1 2 3 1 2 3 0,0 0,991 1,649 1,810 0,041 0,040 0,081 0,961 1,636 1,728 0,037 0,040 0,073 0,2 1,129 1,831 1,997 0,050 0,049 0,115 1,089 1,809 1,909 0,046 0,051 0,107 0,4 1,278 2,037 2,111 0,058 0,060 0,136 1,239 2,024 2,042 0,055 0,062 0,130 0,6 1,459 2,235 2,285 0,069 0,160 0,159 1,420 2,156 2,180 0,065 0,181 0,153 0,8 1,688 2,285 2,289 0,083 0,133 0,135 1,611 2,132 2,168 0,076 0,119 0,129 1,0 1,965 1,906 1,994 0,097 0,101 0,108 1,760 1,816 1,949 0,082 0,093 0,111 1,2 1,610 1,611 2,293 0,078 0,079 0,185 1,542 1,546 2,155 0,072 0,074 0,180 1,4 1,377 1,379 2,177 0,063 0,063 0,179 1,318 1,344 2,042 0,058 0,060 0,175 1,6 1,189 1,193 2,093 0,051 0,052 0,176 1,156 1,156 1,976 0,048 0,049 0,173 1,8 1,037 1,042 1,831 0,042 0,043 0,049 1,021 1,023 1,834 0,041 0,041 0,052 2,0 0,909 0,919 1,649 0,035 0,036 0,040 0,886 0,896 1,642 0,032 0,034 0,041 перемещений. Полученные для различных гармоник решения выстраивались по возрастанию действительной части собственной частоты. Для традиционного конечно-элементного алгоритма число узлов в расчетах составляло ∼ 2,4 ⋅103 .

Сопоставление результатов демонстрирует их удовлетворительное совпадение. В приведенном примере оптимальное решение по критерию (14) имеет место при Z ₀ ^* = Z ₀/ R = 1.

Пример 2. Решалась задача демпфирования при транспортировке цилиндра с опорами, охватывающими его частично (Рис. 1, б ). На рисунке 2 приведены результаты расчета трех первых ω ^* _R и соответствующих им значений ω ^* _I при ϕ=π . При этом варианте опор оптимальное решение имеет место при Z ₀ ^* ≈ 0,6 . Следует заметить, что с точки зрения иллюстрации предлагаемых алгоритмов решения задачи собственных колебаний вязкоупругих тел рассматриваемый вариант опор цилиндра, в отличие от предыдущего, кольцевого, может быть рассчитан только в трехмерной постановке.

Таким образом, в данной работе при решении задачи собственных колебаний кусочно-однородных вязкоупругих тел предложено использование пакета ANSYS в двух вариантах: – первый вариант определяет некоторую последовательность действий на основе пакета ANSYS, и в результате получается алгебраический аналог поставленной задачи; – второй вариант основан на идее представления решения рассматриваемой задачи в виде линейной комбинации собственных форм колебаний соответствующего упругого тела (метод главных координат), которые находятся с использованием пакета ANSYS. При этом удается существенно снизить порядок разрешающей системы алгебраических уравнений, что, в свою очередь, важно для решения частичной проблемы собственных значений.

Для иллюстрации возможностей предложенных вариантов приложения пакета ANSYS к определению и оптимизации диссипативных свойств кусочно-однородных вязкоупругих тел выполнен расчет демпфирующих свойств двухслойного цилиндра при его транспортировке в зависимости от расположения опор. Результаты расчетов показали высокую эффективность предложенной схемы решения задачи, опирающуюся на возможности пакета ANSYS, по сравнению с традиционной схемой метода конечных элементов. Особенно это эффективно для вязкоупругих тел неканонической пространственной формы.

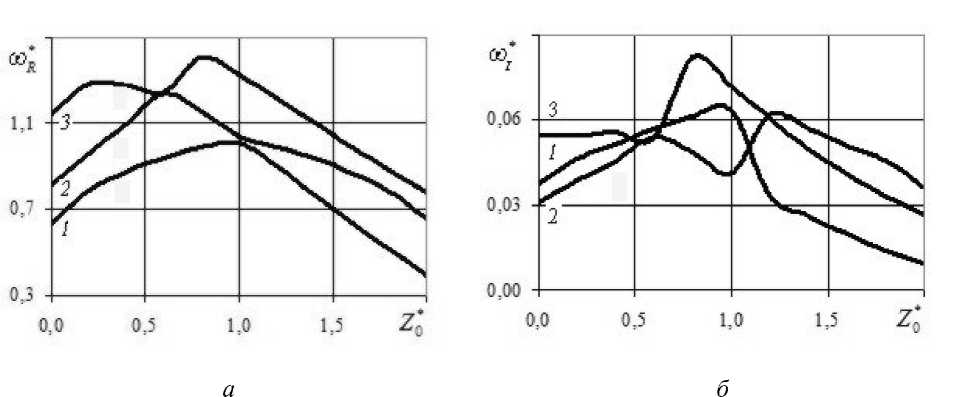
Рис. 2. Зависимость действительной ( а ) и мнимой ( б ) частей собственных частот колебаний двухслойного цилиндра от места расположения опор

Работа выполнена при финансовой поддержке программы фундаментальных исследований Президиума РАН № 11 и Российского фонда фундаментальных исследований (проект № 09-08-99127_р_офи).