Определение собственных мод для гравитационной неустойчивости в газовом диске

Гравитационная неустойчивость является важнейшим фактором, определяющим динамику галактик и свойства структурных подсистем от наиболее крупномасштабных до самых малых, связанных с областями рождения небольших газопылевых облаков и звезд [1]. В работе рассмотрена гравитационная неустойчивость на длинах волн, сравнимых с масштабом неоднородности равновесного газового диска, в приложении к объяснению наблюдаемой спиральной структуры S -галактик.

Глобальные моды в линейном приближении

Рассмотрим динамику малых возмущений 8 f в виде спиральной волны 8 f ( r , ф , t ) = f 1 ( r ) ^х exp(- i ro t ⁺ im ф ) в цилиндрической системе координат ( r , ф ). Для определения структуры собственных мод f ₁( r ) и собственных частот воспользуемся моделью, описанной в работах [2; 3].

На рисунке 1 показаны собственные функции гравитационно неустойчивого диска для заданного равновесного состояния. Характерной особенностью является одновременное существование нескольких неустойчивых мод, которые различаются как пространственной структурой, так и значениями собственных частот го . Соответствующие вещественные и мнимые части собственных частот приведены на рисунке 1.

Для возмущений энтальпии w^r ) и гравитационного потенциала ^ 1 ( r ) :

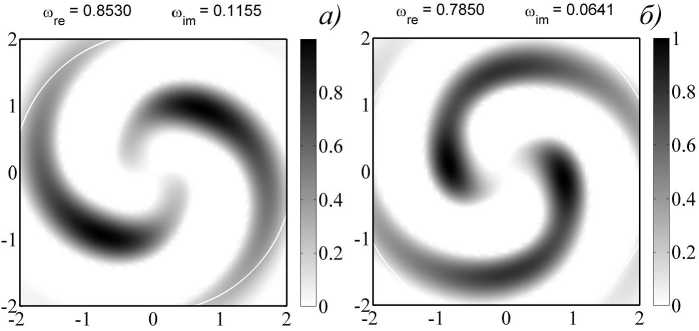
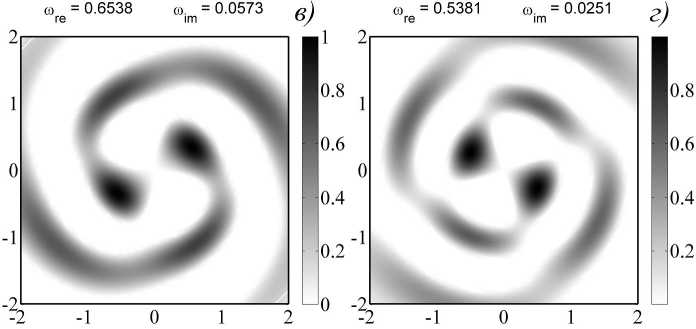
Рис. 1. Структура неустойчивых собственных мод в линейной модели

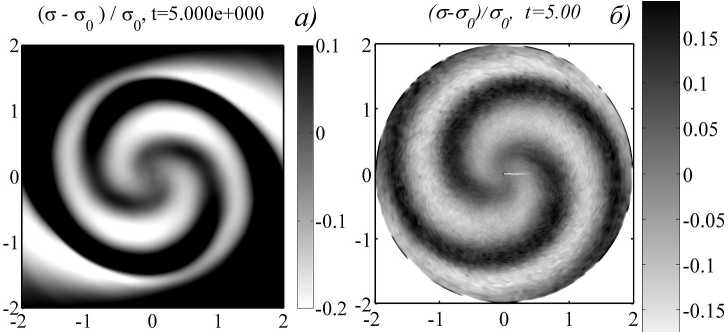
Рис. 2. Структура неустойчивых волн в нелинейных моделях: а ) TVD; б ) SPH

d^ (w, +T,) + Ad (w, +T,) + B (w, + %)-D »1 = 0, dr               dr                          cr где величины A(r), B(r), C(r), D(r) определяются равновесными параметрами диска; cr – скорость звука.

Численное решение нелинейных уравнений

Нами изучена устойчивость гравитирующего газового диска с использованием двух различных численных методов для решения полных нелинейных уравнений газодинамики: TVD-алгоритма и SPH-подхода. Гравитационная сила от газового диска рассчитывалась с помощью метода TreeCode. В качестве исходного начального состояния выбирались равновесные распределения плотности газа, скорости вращения и давления, близкие к тем, которые лежали в основе линейного анализа устойчивости.

На рисунке 2 изображены распределения поверхностной плотности на начальной стадии развития гравитационной неустойчивости для SPH- и TVD-моделей.

Заключение

В рамках линейного приближения реализована численная модель для определения собственных частот гравитационно неустойчивых возмущений в радиально неоднородном газовом диске.

Проведенное сравнение линейного анализа устойчивости с результатами нелинейного моделирования газового диска с учетом самогравитации показало удовлетворительное согласие между радиальной структурой возмущений в случае доминирования двухрукавной моды.