Определение спектров решений краевых задач для направляющих структур с использованием перехода к интегральным уравнениям

Наиболее общими собственными значениями несамосопряженных краевых задач являются ком-плекные значения, соответствующие комплексным волнам (КВ). В открытых направляющих структурах КВ подразделяются на собственные и несобственные [7]. Последние не удовлетворяют условию излучения и описываются фактически решениями неоднородных краевых задач, которые можно классифицировать как полуоднород-ные, поскольку им соответствуют однородные дифференциальные уравнения и неоднородные на бесконечности граничные условия. Понятие «несобственные волны», по-видимому, введено в [7]. Собственные КВ удовлетворяют условию излучения и, соответственно, описываются решениями однородных краевых задач. Другой разновидностью несобственных КВ являются так называемые волны, присоединенные к источнику [8]. Они являются несобственными в силу того, что не могут существовать без источника. Парное возбуждение таких волн приводит к образованию явления комплексного резонанса (КР) [1; 3].

1. Краевые задачи в интегральном представлении

функциями, удовлетворяющими уравнению Бесселя вида:

d 2v + 1 dv + dr2r dr

2 ^

-2- v = 0,

где — = 0, 1, 2, ...; a - поперечное волновое число по радиальной координате.

Сделав замену v(r) = u (r) / Vr, от (1) переходим к уравнению

d 2 u

L ⁽ u ) = 7T⁺ dr

■. ( 1/4 — ^{— 2} ) ]

+      ,2

u = 0.

В результате краевые задачи по радиальной коор-

динате для цилиндрических направляющих структур ставятся на уравнении (2) при граничном условии

u i = 0 ( i = 1, 2, ..., N ),

включающих в себя условие ограниченности поля на оси направляющей структуры, условие непре-

рывности тангенциальных компонент поля на границах между слоями цилиндрической струк-

туры, граничные условия при r ^» для открытых направляющих структур и условия Дирихле и Неймана на идеально проводящих поверхностях.

Оператор L в (2) в общем случае действует [5] в гильбертовом пространстве L ² ( 0, да ) . Функция p ( r ) = ( — ² - 1/4)/ r ² является суммируемой на всей полуоси [0, да ).

Поскольку поперечное сечение слоистой направляющей цилиндрической структуры разбивается по радиальной координате на q подобластей, краевая задача на уравнении (2) решается при од- нородных граничных условиях

U k = 0;    k = 1,2,... N ,

число которых определяется [1; 3] как N = 2 nq , где n – порядок дифференциального уравнения (в нашем случае n = 2).

В случае полуоднородной краевой задачи [1–3], когда при r ^ ж не ставится нулевое граничное условие, некоторые условия (4) могут быть неоднородными [3]. Решения краевой задачи (2), (3) и (4) совпадают [6; 9] с решениями интегрального уравнения Вольтерра:

r

^u ( ^r ) = Z C i Ф i ( ^r ) - J K ( ^r , ^r ' ) u ( ^r ' ) d

i = 1

где K ( r , r ') =

a

P (r')

^(‘J D (r, r); W (r) — вронскиан на фундаментальных решениях уравнения d-u + a2 u = 0; dr2

функция D ( r , r ‘ ) определяется в данном случае как D ( г , г ' ) = ^ф ( г ' ) ф ₂ ( r ) ^-Q i ( г ) ф ₂ ( r ' )| .

Записывая фундаментальные решения уравнения (6) в виде

Ф 1 ( r ) = e ^{a r} ; ф ₂ ( r ) = e - i ^a r ,                           (7)

получим: W ( r ') = - 2 i a ; D ( r , r ' ) = 2 i sin a ( r '- r ) .

Для выполнения граничного условия (3) коэффициенты C_i в (5) представим как:

CC

C ¹ = 2 i ’ C ² = 2 i •

Тогда уравнение (5) будет иметь вид

r u (r) = C sin ar -J

a

sin ^{a( r} - r ) ⁿ² - ^1/4 u ( r • ) dr'. ^a           ( r ' ) ^{2     1 ;}

Рассмотрим связь интегральных уравнений вида (8) с краевыми задачами для двухслойных цилиндрических направляющих структур.

• 2.    Открытый цилиндрический диэлектрический волновод (ОЦДВ)

Радиальная зависимость полей волн ОЦДВ описывается уравнениями (1), (2). В [1–3] показано, что краевая задача (2), (3) в общем случае в области r > a5 имеет решение u(a,r), удовлетворяющее уравнению u (a, r)

e - i a r _ J sinai r - r ) p ( ,. у (a, ,. ) dr ,

r где a5 - значение r, соответствующее наперед заданному 5 > 0, для которого решения уравнения (7) при r ^ ж имеют асимптотическую запись u (a, r ) = e - iar                                            (10)

в областях поперечного волнового числа a : - первая область - Im a >  0; |a| > 5 ;

- вторая область - Im a< 0; a* 0; g ( r )/| a|< 1, (11) откуда следует, что на критических частотах поверхностные волны могут переходить только в несобственные комплексные волны, а собственные комплексные волны могут существовать в областях частот, удаленных от критических частот поверхностных волн. Решения, имеющие асимптотический вид (8), непрерывно продолжаются при r c[ 0 ^»] .

Расположение корней дисперсионного уравнения в плоскости поперечного волнового числа a ₂ внешней области (вне ДВ), соответствующее приведенному выше рассмотрению на основе интегрального уравнения (9), показано на рис. 1.

Разрез на комплексной плоскости a 2 =у 2 + i 5 2 , которому соответствует Р 2 = 0 ( ₽ = ₽ 1 + i ^ 2 - продольное волновое число), проходит по отрицательной мнимой полуоси ( 5 2 <  0) и частично по действительной полуоси у 2 >  0. Он разделяет два листа римановой поверхности комплексной функции в [7-10]. Решения дисперсионного уравнения, изображенные на рис. 1, находятся на верхнем листе римановой поверхности, которому условно соответствует Р 2 <  0. Стрелки на рисунке указывают движение корней при уменьшении частоты. В точке О , в соответствии с (9), поверхностные волны ЕН [1–3] переходят в быстрые несобственные волны (вытекающие) [7–10; 11]. Их поля, в соответствии с (8), нарастают по радиальной координате. В точке А вытекающие волны переходят в собственные комплексные волны, поля которых удовлетворяют условию излучения Зоммерфель-да. В точке В собственные комплексные волны вновь переходят в вытекающие, которые затем (при уменьшении частоты) переходят в медленные несобственные волны. Как показывают численные расчеты, интервал АВ , предсказанный на основе рассмотрения асимптотического решения (8) интегрального уравнения в указанной области его существования, полностью соответствует получаемому из дисперсионного уравнения краевой задачи. Таким образом, предлагаемое асимптоти-

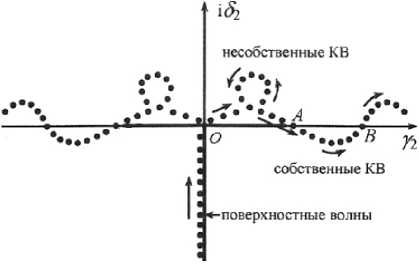
Рис. 1. Корни дисперсионного уравнения волн круглого открытого ДВ в ПЛОСКОСТИ ВОЛНОВОГО числа « 2

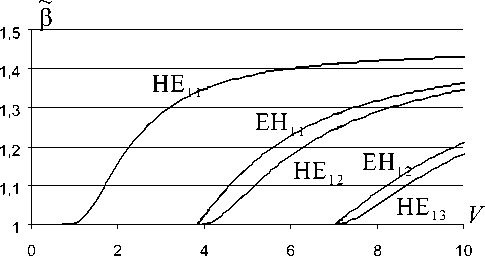
Рис. 2. Дисперсионные характеристики волн ДВ с параметрами: 8 1 = 2.1025, 8 2 = 1

ческое рассмотрение позволяет априорно определить спектр волн исследуемой направляющей структуры.

Во втором и третьем квадрантах комплексной плоскости « 2 решения дисперсионного уравнения располагаются симметрично с вышеуказанными, рис. 1, и соответствуют КВ противоположного направления. Они находятся на нижнем месте римановой поверхности комплексной функции в , которому условно соответствует в 2 >  0. Стрелки на рисунке указывают движение корней дисперсионного уравнения при уменьшении частоты. Совместное возбуждении пар КВ с противоположно направленными фазовыми скоростями приводит к образованию явления комплексного резонанса, соответствующего колебанию, присоединенному к источнику [8].

Отмечено, что в т. О только поверхностные волны ЕН переходят в вытекающие как решения дисперсионного уравнения (аналитически). Для волн НЕ в этой точке дисперсионные характеристики поверхностных волн НЕ при стремлении к критической частоте приближаются к т. О , но не достигая ее в пределе. В [12] показано, что только при введении потерь указанная особенность исчезает: дисперсионные характеристики поверхностных волн НЕ на критических частотах также переходят в характеристику вытекающих волн, то есть в реальных ДВ свойства НЕ- и ЕН -волн качественно совпадают за исключением того, что спектр НЕ -волн включает в себя волну HE ₁₁, не имеющую критической частоты. Таким образом, утверждение о том, что критические частоты поверхностных волн HE1 m + 1 и EH 1 m совпадают, является справедливым лишь при учете потерь.

Проведенное рассмотрение интерпретирует возможность априорного исследования спектров волн направляющих структур на основе сопостав- ления решения краевых задач и интегральных уравнений Вольтерра с использованием асимптотических решений последних.

Определив по предлагаемой методике номенклатуру решений краевой задачи и области их поиска, число решений и их точные значения находим методом вариации фазы [2].

На рис. 2 приведены дисперсионные характеристики гибридных волн ДВ при n = 1, 8 1 = 2.1025, 8 2 = 1. Видно, что критические частоты волн HE1 m ₊ 1 , на которых в ^ л^ , находятся несколько выше критических частот волн EH _{1 m} .

Собственные КВ (интервал АВ , рис. 1) существуют лишь при достаточно большой относительной диэлектрической проницаемости 8 = 8 1 /е2 - С увеличением индекса волны n величина 8 , при которой могут существовать собственные КВ, понижается.

• 3.    Цилиндрический двухслойный экранированный волновод

Интегральное уравнение (5), соответствующее радиальной краевой задаче, в этом случае записывается как

• , х <24         b sin a( r — r 1      х х

u (r ) = Z Ciф i + J-----a----" P (r') u (r') dr'"(12)

i=1

Фундаментальные решения уравнения (6), удовлетворяющие граничным условиям u 1 (r = b ) = 0;   u 2( r = b ) = 0,(13)

в соответствии с (7) имеют вид:

Ф1 = cos ar; Ф2 = cos ar.(14)

Значения a и b – радиусы внутреннего слоя и экрана. Граничные условия (13) соответствуют краевым задачам относительно продольных компонент электрического и магнитного векторов Герца: u ₁ и u ₂ соответственно.

Постоянные коэффициенты C_i в уравнении (12) выбираем таким образом, чтобы обеспечивалось

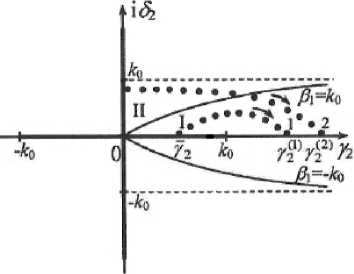
Рис. 3. Корни дисперсионного уравнения волн круглого двухслойного экранированного волновода в плоскости волнового числа « 2

выполнение граничных условий (13). С учетом этого уравнение (12) приобретает вид:

,     . b sin a ( r - r ')

u i — sin a ( b - r ) + I------------- P p ( r ') u 1 ( r ') dr ';

r

,      . b sina( r - r ') , .     , .

u 2 = cos a ( b - r ) + |------------ -p ( r ') u 2 ( r ') dr '.

r

Поскольку решения (14) образуются функциями вида: e±iar, поперечное волновое число, согласно (10), (11), должно быть комплексным и удовлетво- рять условиям:

| a|>§ ;     o ( r )/| a|< 1.                                  (17)

Для волны с продольной зависимостью поля e i ⁽P i ⁺ i P 2 ) z , убывающего при удалении от источника, расположенного в сечении z = 0, должно быть Р 2 <  0. Тогда решения дисперсионного уравнения, удовлетворяющие условиям (17), должны находиться в первом квадранте комплексной плоскости a 2 ( a 2 = у 2 + i § 2 ) . В этом случае значения: Y 2 >  0; § 2 >  0; Р 1 >  0; Р 2 <  0 обеспечивают выполнение равенства У 2 У 2 =-Р^ 2 , получающегося из соотношений, связывающих волновые числа: 22  2

^12^12® — ai 2 +в , где ai 2 — Yi 2 +1§12    попе речные волновые числа во внутреннем и внешнем слоях волновода.

На рис. 3 изображены решения дисперсионного уравнения, которые располагаются в области, определенной на основе интегральных уравнений (15), (16), соответствующих краевой задаче. На рис. 3 кривые Р 1 — ± к ₀ разделяют области быстрых (I) и медленных (II) волн. Разрезы комплексных плоскостей a^ соответствуют значениям |3 2 — 0; к 0 — ®^ ^е 2 ^ 2 .

Из (8), (9) следует, что решения дисперсионного уравнения краевой задачи существуют комплексно-сопряженными парами: a^ и a ^ 2 , что приводит [1] к существованию в двухслойном круглом экранированном волноводе двух пар комплексных волн.

Заключение

Из сопоставления краевых задач интегральным уравнениям Вольтерра получили априорную информацию о спектрах волн двухслойных направляющих структур.

Краевые задачи для двухслойных цилиндрических направляющих структур приведены в соответствие интегральным уравнениям Вольтерра. В целом для данного класса направляющих структур эти уравнения оказываются однотипными, поскольку строятся на основе фундаментальных решений одного и того же уравнения (6). С использованием асимптотических решений интегральных уравнений удается проводить априорное рассмотрение спектров волн направляющих структур, т. е. без решения дисперсионных уравнений краевых задач высказывать предположения о спектре их собственных значений, что позволяет проводить целенаправленные численные исследования.