Определение степени смешивания микроорганизмов с различным временем пребывания в поточных биореакторах

В решении задач интенсификации биофизикохимических процессов в аппаратах непрерывного действия важное место занимает рациональная организация потока суспензии субстрат – микроорганизмы (МКО) с упорядоченным последовательным перемещением клеток МКО, близким к соблюдению возрастных градаций [1–3]. С точки зрения теории процессов и аппаратов – это модель потока полного вытеснения. Данное требование связано с функциональной особенностью микроорганизмов физиологически изменяющихся в зависимости от своего возраста в процессе перемещения по аппарату [4–6].

В ряде биотехнологических производств процесс получения целевого продукта основывается на взаимодействии изменяющихся во времени по функциональным возможностям и физическим свойствам МКО с изменяющимся по составу производственным субстратом, причём эти изменения взаимозависимы [4, 5]. При этом чем больше доля сосуществующих в данном объёме МКО, значительно отличающихся между собой по возрасту, тем менее эффективно протекает биохимический процесс, так как часть клеток, в силу своего физиологического состояния, не может выполнять функцию, заданную технологией на данной стадии. По этой причине не только уменьшается суммарная скорость биохимических реакций, но и снижается качество целевого продукта [5].

Для различных конкретных биохимических производств возрастная граница сосуществующих МКО устанавливается в результате специальных микробиологических исследований по соотношению возраст – функциональное состояние клеток [6]. Эти данные включаются в качестве начальных условий в расчетные уравнения. Так, например, при производстве высококачественных игристых вин резервуарным методом в непрерывном потоке необходимо максимально возможно соблюдать допустимую границу функционально – возрастной совместимости дрожжевых клеток т д = т₂ - т_ъ где ту и т₂ - минимальный и максимальный возраст клеток в рассматриваемом объеме аппарата, т д - допустимая разница в возрасте клеток [5, 7]. Связано это с тем, что на начальной стадии рассматриваемого биохимического процесса, соответственно во входной и центральной зоне аппарата, должно осуществляться брожение, которое могут проводить лишь молодые активные клетки. Одновременно в хвостовой части аппарата (установки) угнетенные возрастные МКО должны через автолиз обогащать субстрат биологически активными веществами, формируя при этом заданные качественные и типичные свойства продукта. В случае же попадания угнетённых клеток в нижние зоны, при движении потока снизу-вверх, последние останутся балластом, так как они уже не обладают бродильной активностью, а процесс автолиза заблокирован консервирующим воздействием сахарозы. Молодые же клетки не могут совершать положительной работы в выходной части аппарата ввиду отсутствия сахарозы в субстрате, они в данном случае будут использовать резервные питательные вещества, обедняя целевой продукт [5, 8].

В связи с тем, что жизненные процессы у микроорганизмов, в частности у дрожжей, особенно в их активной фазе, протекают исключительно быстро (часы) [2, 5, 6], то связь возраста и функционального состояния клеток вполне коррелируют со временем пребывания в аппарате (установке) и могут оцениваться этим параметром. Знание количественного соотношения микроорганизмов различного возраста в данном единичном объеме потока важно для корректировки технологических режимов и решения целевых задач по созданию и оптимизации современной аппаратуры для биотехнологических процессов [7–10].

Несмотря на практическую важность вышеупомянутой задачи [2, 11], в решении которой заинтересованы инженеры, биохимики, биофизики, микробиологи и другие специалисты, она до сих пор не решена [12, 13]. Это объясняется тем, что биохимические процессы, реализуемые в аппаратах с моделью потока диффузионного типа, как правило, описываются нелинейными уравнениями в частных производных, регулярный метод аналитического решения которых отсутствует.

В связи с отсутствием искомого решения в инженерной практике вынужденно пользуются идеализированными моделями, такими, как «идеальное смешение», «идеальное вытеснение». Ниже будет показано, как использовать предлагаемый метод для решения некоторых практически важных нелинейных задач математической физики, встречающихся в биотехнологии.

Исследование

Для решения поставленной задачи будем исходить из уравнения Фоккера–Планка– Колмогорова для функции E ( x , t ) . Согласно [13–17] оно представимо в следующем виде:

—E ( x , t ) + < у— E ( x , t ) = -y E ( x , t )■ D , (1) д t             д x           д x ²

где t – время изучаемого процесса; х – декартова координата, направленная вдоль оси аппарата; D – эффективный коэффициент диффузии (коэффициент продольного перемешивания микроорганизмов в аппарате); ω – средняя по сечению аппарата продольная скорость движения микроорганизмов;

E (x, t)=—q (x, t); q (x, t) - вероятность вы-д t хода микроорганизма из объема аппарата, равного S ■ x, за время t > 0; S - площадь поперечного сечения        аппарата;

1 - q ( x , t ) = p ( x , t ) - вероятность невыхода микроорганизма из указанного объема.

Следовательно, E ( x , t ) - плотность функции распределения микроорганизмов по временам пребывания в объеме S ■ x . По оп-

W ределению т(x) = j tE(x, t) dt - среднее время 0

пребывания микроорганизмов в объеме аппарата, равном S ■ x .

Уравнение (1) представляет собой линейное дифференциальное уравнение в частных производных, которое имеет бесчисленное множество решений. Для выделения единственного решения необходимо к уравнению присоединить начальные и граничные условия. В частности, для полуограниченного канала начальные и граничные условия первого и третьего рода [13], гарантирующие однозначное решение уравнения (1), соответственно, имеют вид:

• 1.    E ( x ,0 ) = 0, x >  0; E ( 0, t ) = J ( t ) ,   (2)

• 2.    E ( x ,0 ) = 0, x >  0 ;

Поэтому, при < 7 ₀₁ <  0,2, с погрешностью

менее одного процента правую часть выражения (5) можно упростить до вида

E 2 ( x , t ) =

to x

^nDt x + to t

exp

( x — to t )

4 Dt

. (6)

E ( x , t ) - —E ( x , t ) to о x

x = 0

где 3 ( t ) - дельта-функция Дирака [18, 19].

На основании вышеизложенного извест-

ными математическими методами можно получить явные выражения для E ( x , t ) -функций, ( г = 1,2):

E ^{1 (} x ^, t ) = 2 n t x ^CXP

( x — to t )

2 Dt

если функция E ( x , t ) удовлетворяет началь-

ным и граничным условиям (2), и

E 2 ( x , t ) =

to exp

'JnDt

( x — to t )

4 Dt

—

to2

2 D

1 — ф

x + tot

2 Dt

to x

D

Прежде чем переходить к определению степени смешения микроорганизмов P_S в том или ином объеме рассматриваемого аппарата, предварительно – для наглядности, выберем три «точки наблюдения»: x = x 1 , x = x ₂ и x = x ₃, где x 1 <  x ₂ <  x ₃ <  L , L - рабочая длина (высота) аппарата. Соответствующие им Е -функции изображены на рисунке, где, например, t = t_P - точка пересечения кривых E ( x 1 , t ) и E ( x ₂, t ) , определяемая из решения уравнения

E ( x 1 , t ) = E ( x 2 , t ) .               (7)

Аналогичным образом, из решения уравнения E (x2, t) — E (x3, t) = 0 определяется значение величины t2,3 . Очевидно, что площади заштрихованных участков на рисунке численно равны PS , т. е. долям сосуществующих микроорганизмов, поступившим в аппарат с потоком жидкости за время т1, т2 и т2, т3 соответственно, где Ti = xi/to, i = 1,2,3. Поэтому tp                м

P S = J E ( x ₂, t ) dt + J E ( x 1 , t ) dt = 0                   t_P

если функция E ( x , t ) удовлетворяет началь-

= 1 + q ( x 2 , t p ) — q ( x 1 , t p )            , (8)

ным и граничным условиям (3).

Здесь ф ( Z ) = ,— V 2 п

Z

г x

J exp —у

dx

инте-

грал вероятности. В формуле (5) последний член неудобен для инженерных расчетов при

малых значениях величины    <7 ₀₁, где

2  2D с01 =---, так как в этом случае аргумент у tox1

интеграла вероятности становится слишком большим. Но при больших значениях Z

2П

exp

Г 1 1

V Z Z ^{3 +}

где было учтено, что q ( x , ~ ) = 1, q ( x ,0 ) = 0.

Итак, для определения степени смешения микроорганизмов, при заданных x ₁ и x ₂ , необходимо знать явное выражение для функции q ( x , t ) и значение величины t_P .

По определению t q (x, t ) = J E (x, t) dt.

Следовательно, q 1 ( ^x , t ) =

1 J 2

V 2 Dt )

1 — ф -j=

V 4i—t

xto exp — "9

exp

q 2 ( x , t ) =

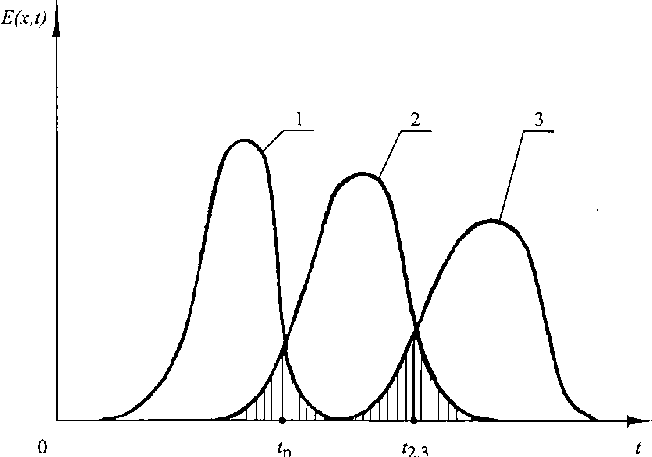
Определение степени смешивания микроорганизмов: 1, 2, 3 – графики Е (x, t)-функции в точках наблюдения х = х 1, х = х 2 , х = х 3 , соответственно

mt

JDDt

4 Dt

.    ( x + m t

1 - ф\ -==

I V2 Dt

, ( x + m t

1 - ф\ -^= ( JlDt

-

mx expD. (10)

Значения величин t_P 1 и t_{P 2} при x ₂ >  x 1 найдем из решения нижеследующих уравнений: E i ( x 2 , t ) - E i ( x 1 , t ) = 0, i = 1,2.

x + x₂ , 2 x 1 x?

t p 1 = \ 2 1 + ^ 01 ---—ln—    , (11)

2 m L       x ₂ - x 1    x 1 _

t p 2 =

x 1 + x 2

2m

x ₁

ln

^{- x} 1

² 3 x ₂ + x 1

₄ 3 x 1 + x ₂

x ₂ x ₁

где индексы «один» и «два» соответствуют начальным и граничным условиям первого и третьего рода.

Выражения (11) и (12), при <7 ₀₁ <  0,2, с погрешностью менее двух процентов упрощаются до вида:

_ x 1 + x ₂

При D = 0 смешение микроорганизмов, поступивших в аппарат в различное время, отсутствует.

Покажем, что и к этому частному случаю формула (8) применима. Действительно, так как при D = 0

E (x, t ) = m3 (x - mt), x -mt где 6(Z) - ступенчатая функция, равная единице при Z > 0 и равная нулю при Z < 0, то согласно формуле (8)

x , + x ₂ где x i <  x ₂, t_P —          .

¹² P 2 m

Вывод

Таким образом, полученные результаты позволяют рассчитать количество сосуществующих микроорганизмов с различным временем пребывания в любом заданном объёме рассматриваемого аппарата и на основании этого достоверно оценивать гидродинамический характер потока реагентов в биореакторах непрерывного действия. По режиму потока осуществляется прогноз эффективности биохимических процессов, реализуемых в данном реакторе.