Определение точности обработки изделий на деревообрабатывающих станках в системе MathCAD

Определение точности работы станков, в том числе и деревообрабатывающего оборудования, является актуальной задачей.

В производстве изделий из древесины одним из основных производственных показателей качества является изготовление изделий с заданной точностью, так как именно точность изготовления позволяет осуществлять взаимозаменяемость деталей и сборочных единиц, что в значительной степени влияет на снижение себестоимости готовой продукции.

При изготовлении изделий из древесины детали и сборочные единицы обрабатывают на станках, как правило, партиями. Партия деталей – это детали, обработанные на одном станке при одной его настройке.

Для получения качественной механической обработки деталей очень важно знать:

• 1)    какую точность обработки изделий позволяет получить данное оборудование (станок);

• 2)    соответствие полученных размеров обработанных изделий заданной точности (допуску).

Эти факторы, как правило, определяются статистическими расчетами.

В настоящее время одним из наиболее прогрессивных способов статистической обработки в производст- венных условиях является использование системы MathCAD на персональном компьютере.

Данная система позволяет создавать алгоритм расчетов с последующим изменением входных параметров и получением новых расчетных значений точности работы оборудования, его настройки и определения процента годных и бракованных изделий при обработке их на любом оборудовании при условии, что вероятность распределения случайных величин подчинено закону нормального распределения.

Рассмотрим данный способ расчета на конкретном примере.

Пример . Выполнить расчет на персональном компьютере основных статистических характеристик партии деталей (50 замеров толщины шипа) при обработке их на шипорезном станке в соответствии с допуском 20у13 и определить:

• •    величину систематической погрешности;

• •    процент годных и бракованных деталей, соответ -ствующих заданному допуску, без учета систематической погрешности;

• •    процент годных и бракованных деталей, соответствующих заданному допуску, с учетом систематической погрешности;

• •    точность обработки деталей на станке - поле рассеивания размеров.

Замеры толщины шипа деталей после их обработки на шипорезном станке приведены в таблице 1.

Таблица 1

Значения замеров толщины шипа, мм

20,28	20,39	20,36	20,33	20,44
20,41	20,38	20,35	20,46	20,30
20,38	20,49	20,32	20,43	20,32
20,40	20,37	20,34	20,45	20,28
20,25	20,36	20,48	20,31	20,42
20,41	20,52	20,36	20,47	20,44
20,55	20,38	20,49	20,43	20,26
20,40	20,51	20,34	20,46	20,43
20,54	20,37	20,48	20,45	20,42
20,39	20,50	20,33	20,44	20,55

Для размера с допуском 20у13 по ГОСТ 6449.1 - 82 + 0,39

найдем предельные отклонения: 20( + о 06 ) , тогда в системе MathCAD запишем и рассчитаем: d:=20.00 – номинальный диаметр, мм;

es:=0.39 – верхнее предельное отклонение допуска, мм;

ei:=0.06 – нижнее предельное отклонение допуска, мм;

dmax:=d+es;

dmax=20.39 – максимальный предельный размер, мм;

dmin:=d+ei;

dmin=20.06 – минимальный предельный размер, мм;

IT:=dmax - dmin;

IT=0.33 – значение допуска, мм;

dsd:=dmin+ ;

dsd=20.225 – среднее значение размера, мм;

n:=50 – количество замеров;

i:=1..n – ранжированная переменная.

p1:=

z2p(x1)dx1

z1

p1=97.00 % – процент годных деталей;

p2:=

z1 p(x1)dx1

a

p2=1.50 % – процент бракованных деталей (размеры шипа меньше заданного допуска);

b p3:= p(x1)dx1                          (7)

z2

Создадим входную таблицу, обозначим ее индексированной переменной хi и введем в нее 50 значений из таблицы 1.

p3=1.50 % – процент бракованных деталей (размеры шипа больше заданного допуска).

Выполним расчет среднего значения хср и среднеквадратического отклонения s по формулам [1] и [2]:

х_i хср:= ∑ i n хср=20.404 мм;

s:=

n-1

⋅∑(xi -xcp)2

i

s=0.076 мм.

Для построения графика функции нормального распределения (рис. 1) запишем предельные значения а и b, зададим значения ранжированной переменной х1 и выполним расчет функции p(x1) по формуле [3].

x1:=a,a+0.01..b – ранжированная переменная;

a:=xcp - 3s;

a=20.176 мм;

b:=xcp+3s;

b=20.633 мм.

p(x1):= (

s

_- (x1 - xcp) ²

1          )⋅e     2⋅s2⋅N2⋅3.14

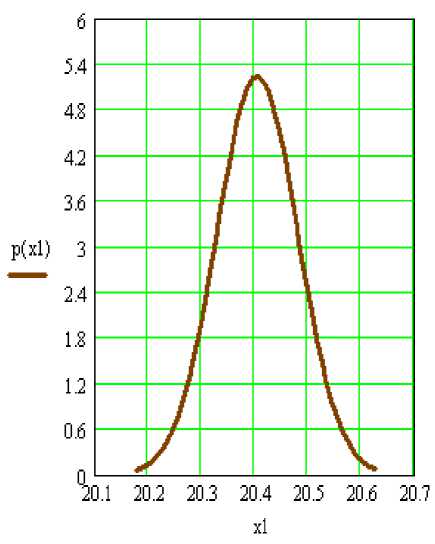
Рис. 1. График функции нормального распределения

Расчет систематической погрешности sp выполняем по формуле [4]:

sp:=xcp - dsd sp=0.179 мм.

Для расчета процента годных и бракованных деталей, с точностью в пределах шести среднеквадратических значений, без учета систематической погрешности (при правильной настройке станка) зададим граничные значения z1 и z2 и выполним расчет по формулам [5], [6] и [7]:

IT z1:=xcp-    ;

z1=20.239 мм;

z2:=xcp+ ;

z2=20.569 мм;

Тогда общий процент брака составит:

brak:=p2+p3;

brak=3.00 %.

Для расчета процента годных и бракованных деталей с учетом систематической погрешности sp (при неправильной настройке станка) зададим граничные условия z3 и z4 и выполним расчет по формулам [8], [9] и [10]:

sp:=xcp - dsd;

sp=0.179 – систематическая погрешность, мм;

IT z3:=dsd-    ;

z3=20.06 мм;

z4:=dsd+ ;

z4=20.39 мм;

∫ z4

p(x1)dx1 ;                          (8)

z3

p4=42.51 % – процент годных деталей;

∫ a

p(x1)dx1 ;                          (9)

z3

p5=0.135 % – процент бракованных деталей (размеры шипа меньше заданного допуска);

b p6:= p(x1)dx1;                          (10)

z4

p6=57.355 % – процент бракованных деталей (размеры шипа больше заданного допуска).

Тогда общий процент брака составит:

brak:=p5+p6;

brak=57.49 %.

Поле рассеивания размеров толщины шипа с вероятностью 99.72 %, а также точность работы станка определяем по формуле [11]:

pr:=6s                                              (11)

pr=0.457 мм.

ВЫВОДЫ

В результате выполненной работы установлено:

• 1.    Точность обработки деталей (поле рассеивания случайных погрешностей) на шипорезном станке соответствует 6s=0.457 мм.

• 2.    Систематическая погрешность составила sp=0.179 мм.

• 3.    Процент годных деталей, соответствующих допуску IT=0.33 мм без учета систематической погрешности (при правильной настройке станка), соответствует 97 %, брак – 3 %.

• 4.    Процент годных деталей, соответствующих допуску IT=0.33 мм с учетом систематической погрешности sp=0.179 мм (при некачественной настройке станка) составил 42.51 %, брак – 57.49 %.

Таким образом, для получения 100 % годных деталей при правильной настройке данного шипорезного станка надо иметь допуск размера больше или равным 0,457 мм, а для получения 100 % годных деталей с допуском размера 20у13 (0,33 мм) станок следует подвергнуть среднему или капитальному ремонту или заменить его на новый.