Определение угловой скорости вращения диска при его восстановлении методом электромеханического деформирования

Одним из основных параметров определения параметров электромеханического деформирования (ЭМД) режущей кромки дисковых почвообрабатывающих орудий является определение угловой скорости ω [1, 2]. Рассмотрим схематическое изображение процесса ЭМД (рис.1а,б). Деталь 2 толщиной 12 (сталь 65Г), жестко прикрепленная к вспомогательной теплоотводящей массе 3, выполненной также в виде диска толщиной 13 (сталь 3), с угловой скоростью го вращается под формующим электродом 3 (твердый сплав Т15К6), к которому приложено напряжение U и давление Р (r1 - радиус цилиндрической части сечения детали; r2 -радиус конической части сечения детали до конечной части затупленной кромки; r3 - радиус теплоотводящей массы; r - средний радиус зоны деформирования; 11 -длина электрода).

Выделим на поверхности обрабатываемой детали окружность радиуса r₀ (4, рис. 1а) и пронижем систему «деталь - теплоотводящая масса» в направлении, перпендикулярном к вышеуказанной поверхности. Тогда получим составной стержень, состоящий из двух контактирующих стержней: стержня из стали 65Г и стержня из стали Ст-3 (пунктирная область, рис. 1б) [3].

Рис. 1. Схематизация процесса ЭМД в динамическом режиме; а) вид сверху; б) поперечное сечение

В первом приближении этот стержень будем считать однородным стержнем длиной 1=12+13 с некоторыми усредненными теплофизическими характеристиками. Считаем, что выделенный условный стержень, двигаясь по окружности (пунктир- ная линия, рис. 1а), через боковую поверхность площади S1=2nr0l нагревается до заданной температуры, распределенной по длине стержня по закону Θ(x). Теплообмен стержня с окружающей средой осуществляется через его торцы.

Температурное поле рассматриваемого стержня T(x,t) ( х- координата, t -время) описывается уравнением:

dT = a’ BdT + кг(6(x)-T)’  00 ’ dt

_ 2

где a =--- - температуропровод- c⋅ρ ность, м2/с;

X - среднее значение теплопроводности, Вт/(м^К);

с - среднее значение удельной массовой теплоемкости, Дж/(кпК);

р - плотность, кг/м³;

k₂ - коэффициент, учитывающий кон-дуктивный теплообмен условно выделенного стержня с окружающей массой материала детали, с - .

Теплообмен условно выделенного стержня, осуществляемый с его торцов с окружающей средой, регламентируется законом Ньютона, то есть:

• - X ^дТ\ = = 0 = а t ) • ( Т, - Т ), х=0, t>0 , (2) ∂ х

• - x ^ х = , = а с t ) • (т - Т ср ) , x=l, t>0 , ⁽³⁾

∂х где а - эффективный коэффициент теплоотдачи, Вт/(м2К).

К моменту начала процесса ЭМД стержень равномерно нагрет до температуры окружающей среды ( Т_ср ):

T\ t = 0 = Т ср , 0 < х < I ; t=0 ,

Требуется определить время t F , за которое точка стержня с координатой х=1₂ достигнет температуры пластической деформации Т дЕФ . Таким образом будет определена и угловая скорость:

ϕ

^ = — , t _F

где ф - угловое расстояние (рис.2), проходимое составным стержнем за время t_F равное t 1 ( t 1 - продолжительность стадии термической подготовки).

На рисунке 2 схематически представлен процесс перемещения составного стержня из начального положения в конечное положение на стадии термической подготовки.

Начальное положение - нахождение составного стержня под областью, обозначенной цифрой 4 на рис. 1а. Это начальная точка - точка вхождения внешней торцевой поверхности составного стержня в зону термического влияния электрода. С момента попадания стержня в эту зону начинается процесс интенсивного нагрева.

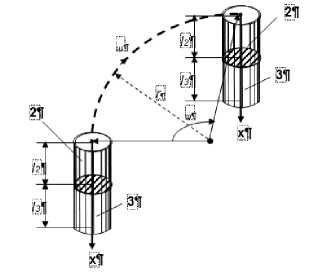
Рис 2. Перемещение составного стержня из начального в конечное положение на стадии термической подготовки [4]

Конечное положение - вхождение участка поверхности детали 4 под формующий электрод. В этот момент времени завершается первая стадия ЭМД - стадия термической подготовки и начинается вторая стадия - стадия пластического деформирования.

Каждый составной цилиндр, находящийся в момент включения экспериментальной установки на своем угловом расстоянии от формующего электрода, будет входить под формующий электрод в индивидуальном тепловом состоянии, которому будет соответствовать свое темпера-

Таким образом, правильный выбор значений основных технологических параметров P,U,I,S, ω, исходя из заданных геометрических размеров восстанавливаемой детали, марки стали и степени износа, обеспечит стабильное восстановление режущей кромки по всей ее протяженности.

турное поле.