Определение упругих констант энергетических материалов на основе экспериментальных данных по механическому воздействию

Одна из ключевых проблем использования энергетических материалов (ЭМ) – это обеспечение безопасности при их хранении и эксплуатации с целью исключения аварийных ситуаций [1– 3] в случае воздействия на них механических и тепловых нагрузок.

Проблемы обеспечения безопасности применения ЭМ усугубляются тем, что основным направлением в развитии ЭМ в настоящее время стало повышение мощности зарядов, которая достигается за счет увеличения энергоемкости и плотности материала. Однако чем мощнее ЭМ, тем более опасными они оказываются в производстве и применении. С ростом мощности возрастает их чувствительность к механическим и тепловым воздействиям, что особенно критично в условиях механических нагрузок.

В настоящее время существуют различные методы оценки чувствительности ЭМ [4–7] на основе расчетно-теоретических исследований поведения ЭМ при механических воздействиях, но они не являются универсальными. Это связано с тем, что различные способы механических и тепловых нагрузок ЭМ могут вызвать различные механизмы инициирования взрывчатых превращений. Одним из таких механизмов может являться формирование разогретого тонкого слоя ЭМ в зоне сдвига, который образуется на границе контакта ЭМ с инертным материалом. Следовательно, разработка математической модели деформирования термопластичных материалов становится еще более актуальной, так как она позволит более точно прогнозировать поведение ЭМ в экстремальных условиях и снизить риски аварий.

Следует отметить, что рассматриваемые энергетические материалы являются многофазными (гетерогенными), что значительно усложняет математическое моделирование реальных гетеро-

Ковалев Ю.М., Лебедев М.А., Маташ В.П., Определение упругих констант энергетических Помыкалов Е.В., Яловец А.П. материалов на основе экспериментальных данных… генных смесей по сравнению с однофазными средами по, как минимум, двум причинам. Во -первых, осложняется описание процессов в отдельных фазах, имеющих место и в однофазных средах. Во-вторых, в многофазных средах проявляются эффекты структуры фазы, эффекты межфазного взаимодействия, и в результате - число возможных процессов, которые должны быть отражены в уравнениях, многократно расширяется.

В эксперименте невозможно разделить измерения параметров отдельных фаз. Поэтому целесообразно при построении математических моделей и проведении расчетов использовать некоторые динамические и термодинамические характеристики материала, полученные из эксперимента, что позволит применять для описания процесса деформирования ВВ модель гомогенной среды.

Целью данной работы является разработка математической модели в приближении гомогенной среды, которая позволит описать упруго-пластические течения и определить упругие константы ЭМ по результатам экспериментов.

Математическая модель воздействия ударника на энергетический материал

Сформулируем задачу, соответствующую экспериментам по воздействию ударника на ЭМ. Стальной цилиндрический ударник, правый торец которого представляет собой полусферу радиуса RH , движется со скоростью V(Vr = 0,Vz = V) и сталкивается с энергетическим материалом, заключенным в цилиндрическую капсулу (рис. 1). Масса ударника равна M. Воздействие ударника на материал приводит к его деформированию (деформацией ударника пренебрегаем) и, следовательно, к изменению термодинамического состояния. При этом кинетическая энергия ударника расходуется на деформацию материала и работу силы трения, поэтому с течением вре- мени скорость ударника уменьшается вплоть до остановки, а запасенная упругая энергия в материале вызывает обратное движение ударника. В эксперименте ударник и образец были располо- жены вертикально, но вклад потенциальной энергии в полную энергию ударника намного меньше, чем вклад кинетической энергии, что позволяет перевести постановку задачи в горизонтальное положение. Таким образом учитывается только значимая составляющая энергии, а именно кинетическая

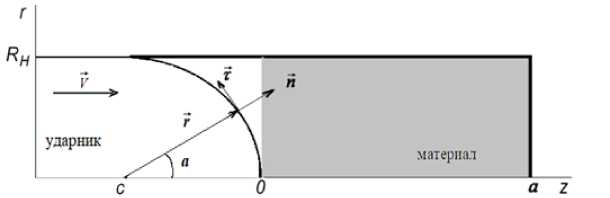
Рис. 1. Схема эксперимента по воздействию ударника на материал

энергия ударника.

Система дифференциальных уравнений механики сплошных сред (МСС), описывающая упруго-пластические течения конденсированных сред в переменных Лагранжа в цилиндрической системе координат, имеет вид:

V

р = -р^; V = V(u-r + u?+uzz);

.   d&rr  dSrz  Srr - S??     .   d^z  dS    Szr pu = —— +--— +--—; pu = —— +--— +——;

dr    dz       r              dz    drr pU = -PV + (SrUrr + SptUw + SzzUzz + 2SrzUrz ) - (Vq);(1)

(1 й^

q = -XV T ;   s 0r = 2 _A l u rr - - - I;

S0z = 2vU - - VI; S?? = -S0 - Szz; S0 = 2u•

Здесь р , u i - массовые плотность и скорость, u _ik - тензор скоростей деформаций, V - объём, & _ik - тензор напряжений, P , S_ik - шаровая часть и девиатор тензора напряжений, U - удельная внутренняя энергия, T - температура, q = -XV T - тепловой поток, описываемый законом Фурье, X - коэффициент теплопроводности.

Для описания пластических течений применялась модель Прандтля–Рейса [8, 9], в которой явно фигурирует тензор скоростей пластических деформаций:

S ik = 2 . U - u p ) ,                                 (2)

где v _ik = v _ik - v_u8 _ik /3, u pp - тензор скоростей пластических деформации, который связан с напряжениями уравнениями Мизеса U p = S_ik / А , Л- модуль пластичности, ц - модуль сдвига. Выражение (2) отражает тот факт, что за упругие напряжения отвечают только упругие деформации.

Модуль пластичности находится из выражения

1/ Л = 3 S U .

^{2   Y} 0²

Из уравнений Мизеса и (2) следует уравнение для тензора девиатора напряжений:

S ik + S ik /p^P = 2 U ,                               (3)

где p^p = Л/ 2 / ./ - время релаксации упругих напряжений за счет пластических течений (максвелловское время релаксации).

Данная система дополняется уравнениями состояния материала [10, 11] и граничными условиями, которые учитывают взаимодействие ударника с материалом. Для решения системы уравнений (1) применялся метод решения системы уравнений механики сплошной среды, описанный в [12].

Режим взаимодействия ударника с материалом задается следующим образом. Положим, что ударник меняет только направление скорости движения материала без изменения его модуля, что соответствует абсолютно упругому взаимодействию.

Пусть найденная из уравнений МСС (1) скорость материала вблизи поверхности ударника равна v ( v _r, v _z ) . При контакте с ударником направление вектора скорости изменяется U ( U r U _z ) , но U = и . Новое направление вектора скорости U находится из условия непроницаемости на поверхности ударника:

u'n = ( U' n ) = 0,                                              (4)

где u' = U - V - вектор относительной скорости, n (nr = sin a, nz = cos a) - нормаль к поверхно- сти ударника.

Таким образом, сохранение модуля скорости вещества при взаимодействии с ударником и условие непроницаемости (4) позволяют записать систему уравнений:

U r sin a + U _z cos a = V cos a ;

U ² + U = v ² .

Решение системы (5) позволяет вычислить U ( U r U _z ) , а также тангенциальную компоненту скорости uT = ( u^f т ) :

U r = V _n sin a + cos a^v² - V n ; v^f_z = V _n cos a - sin a^v² - V n2 ; u'_T = ^v² - V n + V sin a ,    (6)

где V_n = V cos a , f ( т _г = cos a , t _Z = - sin a ) - тангенциальный орт.

В случае, когда скорость материала мала, то есть v <  V_n , он увлекается ударником. В этом случае полагается v = V_n .

Выражения (6) представляют собой граничные условия на поверхности ударника.

За время Д t движущаяся с относительной скоростью u _T точка поверхности материала пройдет по поверхности ударника путь Д 1 = u _TД t и окажется в точке, радиус-вектор которой будет иметь с осью 0 z угол a + Дa , где Дa = Д 1 / R H .

Таким образом, в момент времени t + Д / новые координаты рассматриваемой точки поверхности материала будут равны r = R H sin ( a + Дa ) ; z = R H cos ( a + Дa ) , а направление относитель-

Ковалев Ю.М., Лебедев М.А., Маташ В.П., Определение упругих констант энергетических Помыкалов Е.В., Яловец А.П. материалов на основе экспериментальных данных… ной скорости будет определяться новым тангенциальным вектором т (тг = cos (а + Ла) ,Tz =-sin (a + Ла)). Компоненты скорости материала на поверхности ударни- ка определяются по формулам (6) с углом а + Ла .

При скольжении образца по поверхности подложки в результате работы силы трения их контактная граница разогревается.

По абсолютной величине сила трения, действующая на единицу контактной поверхности, имеет вид

Ff = kfSn , Sn = S,n, = ^ikniknk , где kf - коэффициент сухого трения, где Sn > 0 - сила реакции подложки на единицу площади. Сила трения направлена вдоль контактной поверхности против тангенциальной составляющей вектора скорости образца ит .

Работа силы трения приводит к нагреванию трущихся поверхностей. Тепловой поток, возникающий за счет работы силы сухого трения, имеет вид qf =( Fu )=

' k f s n. u , s n >  o; o, s n ^ o.

Генерируемое на контактной границе тепло распространяется в объемы подложки и образца. Поскольку в общем случае материалы подложки и образца разные, то будут различными и тепловые потоки.

Пусть материал подложки имеет массовую плотность р1 , удельную теплоемкость C, ко эффициент теплопроводности N1, а материал образца - соответственно р2 , C2 , Х2. Соответственно потоки тепла в подложку и образец обозначим через q1 и q2, причем qf = q1 + q2 . Будем искать потоки q и q .

Воспользуемся выражением для температуры поверхности тела под воздействием заданного теплового потока [13]:

T( t ) =

L q i( ; ‘L, _df_+T. n n ^j x-       dt ^{+   ;}

T2 ( t ) =

X г   q2(t')N2 Л 0 Z; (t - t')

■dt ' + T_o ,

где To - начальная температура среды, N1, /1 и N2, х2 — коэффициенты теплопроводности и температуропроводности сред. Представим q2 = ^qf, q1 = (1 - в) qf, где в - доля распространяющегося в образец теплового потока. Из условия равенства температур на контактной поверхности T (t ) = T2 (t) из выражений (9) следует в =

1 ₊   P 1 C N 1

\ ^р2^C 2 ^N 2

л - 1

В литературе формула (10) известна как формула Шарона. Она справедлива при описании нагрева поверхностей при сплошном фрикционном контакте [14].

Температуру контактной поверхности трущихся материалов с найденной величиной в (10)

можно найти из любого выражения из (9).

Движение ударника в данном случае является одномерным и определяется упругой силой, rc действующей на погруженную в материал поверхность ударника  Fz = 2п jsz (r) rdr,

S _z = a _zzn_z + ^ _zrn_r - поверхностная сила, a _lk - компоненты тензора напряжений, n ( n_r = sin ( a ) , n_z = cos ( a ) ) - нормаль к поверхности ударника, r c - координата границы контакта материала с ударником, а также силой трения. Поскольку вектор силы трения направлен по касательной к поверхности ударника, то наиболее просто учесть влияние силы трения на движение ударника можно путем вычитания из кинетической энергии ударника работы силы трения. Таким образом, уравнение движения ударника с учетом упругой силы имеет вид:

MV = F z (t ).

Полагая, что на некотором малом временном интервале движение ударника происходит с постоянным ускорением, нетрудно из (11) записать выражения для скорости ударника в момент t + M :

Работа силы трения (8), совершаемая за время Д t на всей контактной поверхности ударника, приводит к убыли кинетической энергии ударника. Исходя из сказанного, можно записать выражение для скорости ударника с учетом работы силы трения в виде:

V (t + Д ) =

V ( t ) +— k t\ - — M t f q/dr. ^{k 7} M J M ^J_o f

Пространственное положение ударника полностью описывается координатой центра сферической поверхности z_c . Изменение этой координаты находится из выражения

zc (t + Д ) = zc (t) + 0.5 (V (t + Д ) + V (t ))M.

Таким образом, кинетическая энергия ударника идет на изменение внутренней энергии материала и работу силы трения, что приводит в конечном итоге к остановке ударника. С этого момента запасенная упругая энергия в материале приводит к его разгрузке и часть этой энергии идет на движение ударника в обратном направлении. В этом сила трения будет увлекать ударник, то есть в выражении (12) последний член под корнем будет со знаком плюс.

Определение упругих констант энергетического материала

Большинство изделий, содержащих бризантные ЭМ, имеют различную структуру, и подобрать упругие константы, которые адекватно описывают поведение образца при механических нагрузках, проблематично. В данной работе для определения констант используются данные о распределении глубин отпечатка ударника на поверхности энергетического материала, полученные в ходе эксперимента [15] совместно с численным моделированием. Постановка эксперимента представлена ранее на рис.1. Экспериментальные данные содержат информацию о глубине внедрения ударника (пуансона), скорости ударника и реакции образца ЭМ. В таблице представлены данные серии экспериментов по ударному воздействию на октогенсодержащий ЭМ.

Данные серии экспериментов по ударному воздействию на октогенсоде			ржащий ЭМ
№ опыта	Максимальная глубина проникновения пуансона в образец, мм	Скорость проникновения пуансона в образец, м/с	Результат
1	3,3	13,26	взрыв отсутствует
2	4,83	27,5	взрыв
3	5,31	29,7	взрыв
4	5,40	26,9	взрыв
5	3,08	11,18	взрыв отсутствует

На рис. 2 представлены динамики погружения пуансона в ЭМ для экспериментов № 1 и 5, эксперименты были выбраны таким образом, что в них отсутствует взрыв, что позволяет определить упругие константы ЭМ.

Как видно из рис. 2 эксперимента № 5 на момент времени ~0,45 мс происходит повторное погружение пуансона. Данный эффект связан с тем, что ударник сообщает повторный импульс пуансону и происходит повторное погружение в ЭМ. Так как для эксперимента № 1 отличительной особенностью является отсутствие взрыва и повторных ударов, таким образом, на основании данного эксперимента проводилось определение упругих констант образца ЭМ с помощью численного моделирования.

Ковалев Ю.М., Лебедев М.А., Маташ В.П.,

Определение упругих констант энергетических

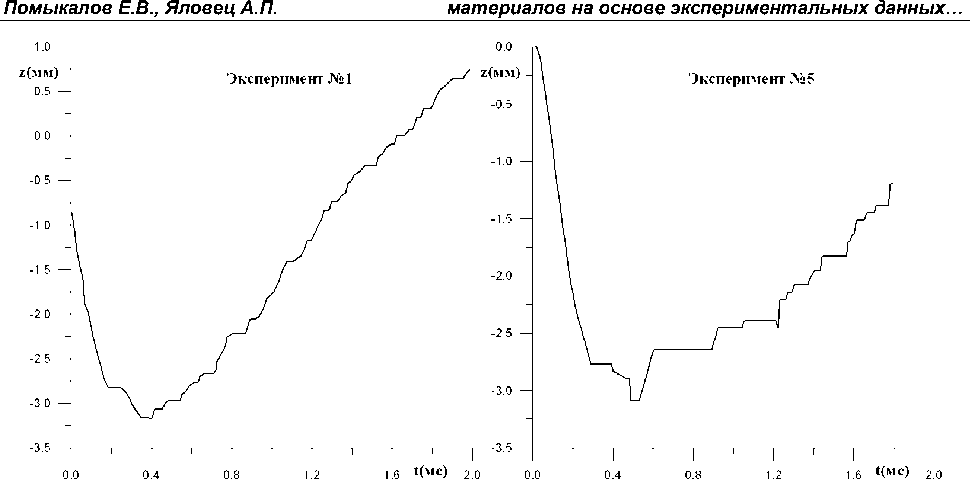
Рис. 2. Динамика погружения пуансона, полученная в ходе экспериментов

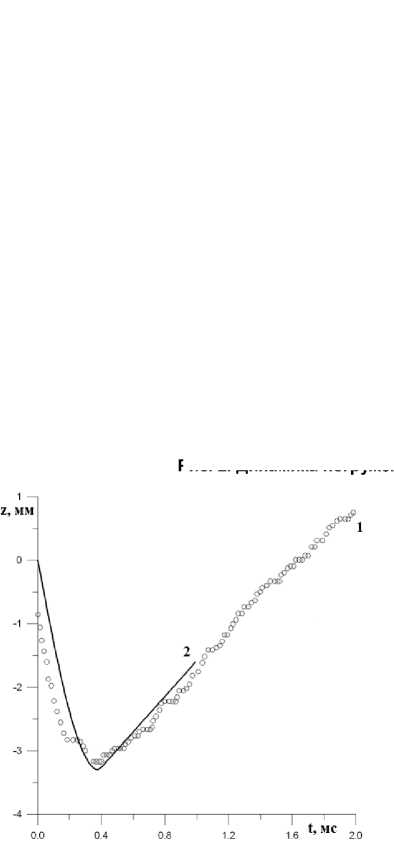
Рис. 3. Сравнение динамики погружения пуансона в эксперименте № 1 с результатами численного моделирования: 1 – эксперимент; 2 – расчет

На рис. 3 представлены графики зависимости глубины погружения от времени нагружения для скорости пуансона из эксперимента № 1. Моментом окончания расчета является время отрыва пуансона от образца ЭМ. Момент времени был выбран так, что отразившийся от поверхности ЭМ ударник обеспечил релаксацию упругих напряжений в ЭМ. В этом случае геометрия отпечатка оставалась в дальнейшем неизменной. В литературе коэффициент трения ЭМ варьируется от 0,2 до 0,4 [16]. Поэтому расчеты проводились при осредненном значении коэффициента трения k f = 0,3.

Анализ полученных профилей и экспериментальных данных показал, что «кратер», полученный в ходе численного моделирования с упругими константами Y = 0,0845 ГПа и µ = 18 ГПа, наиболее близок к геометрии поверхности ЭМ после взаимодействия с ударником. Также угол наклона прямой соответствующей остаточной скорости совпадает с экспериментом.

Таким образом, результаты расчетов глубины внедрения пуансона при скорости ударника 13,26 м/с не противоречит данным, полученным в эксперименте, что подтверждает адекватность найденных упругих констант образца ЭМ.

Выводы

По результатам, представленным в работе, можно сделать следующие выводы:

• 1.    Предложенная математическая модель, основанная на системе уравнений механики сплошных сред и включающая модель Прандтля–Рейса для описания пластических деформаций, продемонстрировала высокую точность в описании экспериментальных данных.

• 2.    На основе анализа экспериментальных данных по динамике погружения пуансона в окто-генсодержащий ЭМ были определены упругие константы материала: модуль Юнга Y = 0,0845 ГПа и модуль сдвига μ = 18 ГПа. Эти значения хорошо согласуются с экспериментальными результатами, что подтверждает адекватность предложенной модели.

• 3.    Предложенная в работе математическая модель может быть использована для анализа других типов ЭМ и оптимизации их состава с целью снижения чувствительности к внешним воздействиям.