Определение усилий мышц и реакций в суставах при движении нижней конечности в тренажере с отягощениями

Для исследования адаптационных процессов восстановления костных тканей нижней конечности, активно протекающих после операции или травмы, необходимо знать текущее напряженно-деформированное состояние восстанавливаемой кости и, следовательно, нагрузки на кость. Настоящее исследование направлено на определение усилий мышц и реакций в суставах бедра и голени, расположенных горизонтально в положении пациента лежа на спине в тренажерном устройстве с отягощениями. Выбор горизонтального положения конечности обусловлен тем, что при сгибании конечности из её горизонтального положения суммарные мышечные нагрузки на бедро достигают наибольших значений [1], активизирующих адаптационную деятельность клеток по перестройке костной ткани [ 2 ] . Анализ решения прямой задачи динамики нижней конечности в данном тренажерном устройстве показывает [1], что динамические составляющие нагрузок малы в течение всего периода восстановительного движения. Это позволяет в первом приближении определять усилия мышц, решая соответствующую задачу статики. Статическая неопределимость задачи преодолевается с помощью известного в строительной механике метода перемещений, распространенного на проблемы биомеханики Г.Н. Колесниковым [ 3 ] .

F 12 Kz     K y     в X                 K x     ' F 12 R x                              ' K x R y   F    F Y         1 F 3   5    F 4   F      Q x ' K y Z R z    F 2 G   F 6 F 7 K z '    Q z Qy

F 10   F 11    F 12''    Qz P F 13 F 9         Q y                      F тр F 14 F 7    Qx      G 2          G 3 N

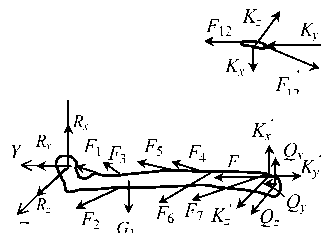
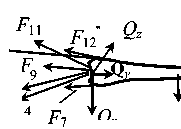
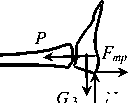
Рис. 1. Расчетная схема нижней конечности: а - бедро, б - голень, в - коленная чашечка, F k _k 114 - усилия мышц, G 1 2 3 - силы тяжести сегментов конечности, R , Q , K - реакции суставов и коленной чашечки, соответственно, F, P - силы натяжения нитей отягощениями, F_mp - сила трения, N - реакция опоры

Нижняя конечность представляется системой трех твердых тел - бедро, голень со стопой и коленная чашечка. Мышцы конечности моделируются упругими прямолинейными нитями, суставы - сферическими шарнирами, суставные хрящи - упругими сферическими оболочками. Жесткости мышц и хрящей считаются известными. Рассматриваются все мышцы, участвующие в актах сгибания и разгибания в коленном и тазобедренном суставах, всего 14 мышц. Точность найденных мышечных усилий оценивается путем сравнения значений их суммарных моментов и реакций в коленном и тазобедренном суставах со значениями этих величин, полученных решением прямой задачи динамики [ 1 ] .

Расчетная схема

Расчетная схема нижней конечности (рис. 1) состоит из трех абсолютно твердых тел: бедра, голени вместе со стопой и коленной чашечки. В рассматриваемой системе сил учитываются усилия следующих мышц: F 1 - m. Iliopsoas (подвздошно-поясничная мышца), F 2 - m. gluteus maximus (большая ягодичная мышца), F 3 - m. pectineus (гребенчатая мышца), F ₄ - m. adductor longus (длинная приводящая мышца), F 5 - m. adductor brevis (короткая приводящая мышца), F 6 - m. adductor magnus (большая приводящая мышца бедра), F 7 - m. adductor minimus (малая приводящая мышца бедра), F 8 - m. semimembranosus (полуперепончатая мышца), F 9 - m. gracilis (тонкая мышца), F ₁₀ - m. tensor fascia lata (напрягатель широкой фасции), F 11 - m. sartorius (портняжная мышца), F ₁₂ - m. rectus femoris (прямая мышца бедра), F ₁₃ - m. biceps femoris (двухглавая мышца бедра), F ₁₄ - m.semitendinosus (полусухожильная мышца). Усилие в связке lig. patellae обусловлено действием прямой мышцы бедра и обозначено на схеме (рис. 1) векторами F 2 и F .

Мышцы с усилиями F 17 начинаются на костях таза и крепятся к бедренной кости. Точки исхода мышц с усилиями F 8 _|4 также расположены на тазовых костях, однако, их точки прикрепления располагаются на большеберцовой и малоберцовой костях. Направления мышц в пространстве определяются по координатам их точек исхода

Таблица 1

Величины средних площадей поперечных сечений мышц и их длины [ 6 ] ___________

№	Названия мышц	A , см2	L , мм
1	подвздошно-поясничная	11,75	157,0
2	большая ягодичная	36,28	213
3	гребенчатая	5,65	122,3
4	длинная приводящая	10,97	263,0
5	короткая приводящая	8,50	157,0
6	большая приводящая	8,7	273,0
7	малая приводящая	9,55	324,0
8	полуперепончатая	8,56	381,0
9	тонкая	4,21	419,0
10	напрягатель широкой фасции	7,28	488,0
11	портняжная	3,06	592
12	прямая мышца бедра	10,06	525
13	двуглавая мышца бедра	11,08	387
14	полусухожильная	7,35	457

( origin points ) и точек прикрепления ( insertion points ) в лабораторной системе осей координат XYZ . Данные координаты вычисляются по локальным координатам этих точек (оси локальных систем координат связаны с костями, на которых расположены точки прикрепления мышц), приведенным в работе [ 4 ] . Жесткость мышц вычисляется по формуле

EA

• ⁵ = Т ’

  где E – модуль упругости; А – средняя площадь поперечного сечения мышцы; L – длина мышцы. Модуль упругости для всех мышц принимается одинаковым и равным 3000 Па [5]. Величины длин мышц и средних площадей их поперечных сечений взяты из работы [6] и приведены в табл. 1.

Средние модули упругости хрящей поверхностных слоев головки бедренной кости и большеберцовой кости составляют 0,931 МПа и 0,113 МПа [7], соответственно. Значения внешних сил, действующих на конечность, принимаются аналогичными принятым в статье [1]: G 1 =73,7 H, G 2 =28 H, G 3 =17,4 H, P =70 H, F =30 H, N =40 H, F тр =8 Н.

Таблица 2

Значения усилий активных мышц и давлений в суставах в горизонтальном положении конечности

Усилия мышц, давления и моменты в суставах	Величины сил (Н) и моментов (Нм)
	Статический анализ	Динамический анализ [ 1 ]
Подвздошно-поясничная мышца	265	230
Прямая мышца бедра	41	0
Двуглавая мышца бедра	0	110
Тонкая мышца	7	-
Полуперепончатая мышца	12	-
Портняжная мышца	30	-
Напрягатель широкой фасции	12	-
Давление таза на головку бедра	395	295
Давление большеберцовой кости на бедренную кость	149	245
Давление надколенника бедренную кость	39	-
Суммарный момент усилий мышц в тазобедренном суставе	6,8	7,5
Суммарный момент усилий мышц в коленном суставе	5,26	5,25

Решение и анализ результатов расчета

Для решения задачи используются 11 уравнений равновесия (по 4 для бедра и голени и 3 для коленной чашечки) и 23 определяющих соотношения упругости для мышц и хрящей (14 для мышц и 9 для хрящей). Предполагается, что нагружение мышц начинается из состояния полного их расслабления, поэтому начальные деформации мышц D 0 [ 3 ] , естественно, принимаются равными нулю. При анализе решения следует считать, что мышцы удовлетворяют условию односторонних связей

^Fk , к =Ш >  °. (2)

В результате расчета установлено, что условию (2) удовлетворяют 7 из 14 учитываемых мышц. В табл. 2 представлены значения усилий активных мышц, давлений в суставах и давления коленной чашечки на бедро в горизонтальном положении конечности. Для оценки полученного решения в третьем столбце таблицы приводятся значения этих же величин, полученные решением прямой задачи динамики [ 1 ] .

Из анализа полученных результатов следует, что квазистатический расчет избыточной системы с односторонними связями позволяет объективно установить все активные мышцы конечности, участвующие в данном акте движения. В то же время при решении первой задачи динамики активные мышцы выбираются субъективно. Данные табл. 2 показывают, что состояние равновесия конечности достигается действием семи мышц как сгибателей, так и разгибателей, в то время как ранее [1] предполагались активными только силы, сгибающие конечность (подвздошнопоясничная мышца и двуглавая мышца бедра). Однако усилия подвздошно-поясничной мышцы в первом и во втором случаях близки по значению, что говорит об оправданном предположении об активности только этой мышцы при сгибании конечности в рассматриваемых условиях.

Значения же усилий других мышц значительно отличаются. Прямая мышца бедра ( m. rectus femoris ), прикрепленная к тазовой кости и коленной чашечке, действует на бедро через надколенник силой K= 32 Н и стремится разогнуть голень усилием F ₁₂=41 Н в связке lig. patellae. Вопреки предположениям, ранее сделанным в работе [ 1 ] , двуглавая мышца бедра ( m. biceps femoris ) в данном положении конечности вообще не является активной. Голень сгибается усилиями четырех мышц: m. gracilis (приводящая тонкая мышца), m. semimembranosus (полуперепончатая мышца), m. sartorius (портняжная мышца) и m. tensor fascia lata (напрягатель широкой фасции). Усилия этих мышц и прямой мышцы бедра значительно увеличивают (на 33 %) давление таза на головку бедра. Давление между бедром и большеберцовой костью, наоборот, существенно уменьшается (на 39 %), что связано с пассивностью двуглавой мышцы бедра. Однако общее давление на дистальный отдел бедра несколько возрастает благодаря давлению коленной чашечки.

Количественная оценка обоснованности рассчитанных в данной работе усилий мышц может быть сделана путем сравнения значений их суммарных моментов со значениями, полученными из уравнений Лагранжа 2-го рода в работе [ 1 ] . Величина суммарного момента усилий мышц в тазобедренном суставе при учете их активного укорочения несколько меньше (на 9,3 %) величины, полученной в работе [ 1 ] . Это уменьшение объясняется действием силы давления коленной чашечки, момент которой противоположен моменту усилия подвздошно-поясничной мышцы. Суммарные моменты от усилий мышц в коленном суставе в обоих случаях практически одинаковы. Следовательно, можно утверждать, что полученное выше квазистатическое решение удовлетворяет с точностью до величины динамической составляющей уравнениям Лагранжа 2-го рода.

При анализе перемещений учитывается предельный характер рассматриваемого равновесия конечности, в котором мышцы нагружены изометрически и их дальнейшее активное сокращение вызовет движение конечности и, следовательно, уменьшение их длин. Поскольку полная длина мышцы не изменяется, активное её сокращение по величине равно пассивному удлинению. Следовательно, уравнение совместности перемещений в форме (2) [3] необходимо изменить, опустив D ₀ . В результате получим

C^TU = D , (3) где C^T - транспонированная матрица коэффициентов при силах в уравнениях равновесия системы, U - вектор перемещений. Кроме того, из постоянства длин активных мышц следует, что точки их прикрепления к костям перемещаются перпендикулярно линиям действия их усилий.

Заключение

Определены активные мышцы и величины их усилий в горизонтальном квазистатическом положении равновесия нижней конечности, совершающей реабилитационные движения при положении пациента лежа на спине в тренажерном устройстве с отягощениями. Полученные усилия мышц удовлетворяют с точностью до величин динамических составляющих уравнениям Лагранжа 2-го рода и, следовательно, являются обоснованными. Из анализа полученных результатов следует, что квазистатический расчет избыточной системы с односторонними связями, позволяет объективно установить все активные мышцы конечности, участвующие в данном акте движения. Тогда как при решении первой задачи динамики активные мышцы выбираются субъективно на основании общих анатомических данных действия мышц конечности, что может привести к качественно ошибочным результатам.