Определение вектора новой промышленной политики на основе неошумпетерианской теории

DETERMINATION OF THE VECTOROF NEW INDUSTRIAL POLICY ON THE BASISOF NEO-SCHUMPETERIAN THEORY

Alexander I. Tatarkin

Institute of Economics of the Ural Branch of the Russian Academy of Sciences

• 29,    Moskovskaya st., Ekaterinburg, 620014, Russia

Oleg S. Sukharev

Institute of Economics of the Russian Academy of Sciences

• 32,    Nakhimovsky prospect, Moscow, 117218, Russia

Perm State University

• 15,    Bukireva st., Perm, 614990, Russia

Ekaterina N. Strizhakova

Bryansk State Technical University

• 7,    50-letiya Oktyabrya Bulvar, Bryansk, 241035, Russia

Неошумпетерианская теория раз- вития: «созидательное разрушение» и «комбинаторное наращение»

Экономическое развитие по Й. Шумпетеру предстаёт в виде процесса осуществления новых комбинаций – создания новых благ, услуг, методов производства, рынков сбыта, источников сырья, монопольного положения, проведения реорганизации [1, c. 132]. Важным элементом, вытекающим из его теоретических построений, выступает условие, отражаемое во многих современных эволюционных моделях. Говоря современным языком, инновация реализуется за счёт отвлечения ресурсов у консерватора в пользу предпринимателя-новатора. Однако противоречивость изложения Й. Шумпетером своих взглядов обнаруживается в трактовке развития в работе «Теория экономического развития» и принципа «созидательного разрушения» в исследовании «Капитализм, социализм и демократия».

В первой работе говорится о развитии как новом использовании труда и земли, причём осуществление новых комбинаций происходит посредством изъятия труда и земли из прежних сфер применения. Новая комбинация забирает средства производства от старой комбинации – так происходит развитие [1, c. 134, 168]. Однако при неоднородном капитале и интерспецифическом ресурсе современной индустрии развитие так происходить уже не может, поскольку под новую комбинацию не подойдут старые средства производства. В этой же работе позже отмечается, что новые комбинации возникают самостоятельно, рядом со старыми комбинациями, а не занимают их место. Более того, они конкурируют со старыми комбинациями [1, c. 332].

Во второй работе «Капитализм, социализм и демократия» формулируется принцип «созидательного разрушения», который как раз описывает заимствование ресурса у старых новыми комбинациями, посредством чего наблюдается их ослабление («разрушение»). Новые комбинации могут вытеснять старые комбинации, но могут существовать параллельно. Вероятна ситуация, что на какой-то фазе развития домини- рует сначала старая комбинация, затем растёт значение новой комбинации, появившейся некоторое время назад, но не создавшей себе сразу доминантного положения. Возможен вариант такого развития, когда сразу начинает доминировать новая комбинация, но по истечении некоторого времени старая комбинация возвращает своё доминантное положение. Как правило, новая комбинация должна забрать необходимые ей средства производства из той или иной старой комбинации [1, c. 134].

Интересно отметить, что совокупный результат развития может быть таким, что темп роста при таком перераспределении факторов производства может понизиться, в отдельных случаях очень существенно. Однако нельзя отказывать новой комбинации в том, чтобы под неё создавался ресурс – новые средства производства, что само по себе уже означало бы первую фазу воспроизводства новой комбинации. Эта ситуация в большей мере отвечает режиму экономического развития, который наблюдается не в эпоху Й. Шумпетера, а в настоящее время. Сегодня средства производства и технологии стали очень специализированными: их применение ограничивается конкретным видом деятельности, и в другом производстве они могут быть применены с невысокой вероятностью и эффективностью. Это накладывает существенные ограничения на применение этих средств производства в развитии новых комбинаций, которые задают и новый уровень качества относительно применяемой технологии и средств производства (фондов, площадей, оборудования и т.д.). К тому же сильным фактором роста стали институты и их изменение, которое в настоящее время происходит с высокой скоростью [2]. Региональные системы детерминируются институтами саморазвития [3; 4]. Структурные ограничения становятся своеобразными институтами экономического роста. В этих условиях представление о развитии как о появлении комбинаций, отвлекающих ресурс от существующих возможностей, является недостаточным. Развитие может происходить за счёт различной комбинации факторов, причём создание нового ресурса, в том числе за счёт объединения технологических возможностей, составляют суть принципа «комбинаторного наращения». Фактически это режим развития без отвлечения ресурса от старых комбинаций. Этот режим можно продемонстрировать, анализируя инвестиции в традиционные и новые технологические возможности.

Записав выражения для инвестиций в старые и новые технологии, учтя параметр, характеризующий скорость отвлечения ресурса (α) и скорость создания нового ресурса (μ), пополняющих инвестиции в новые технологии, запишем: In = αIs + μIn. То есть инвестиции в новые технологии (комбинации) складываются из отвлечённого ресурса от старых технологий (долю обозначает величина α) плюс наращённый (созданный) ресурс, идущий на новые технологии (долю обозначает величина μ). Изменение этих параметров и даст скорость отвлечения и создания ресурса. Если скорость отвлечения ресурса α полностью символизирует шумпетеровский подход и, по сути, означает принцип «созидательного разрушения», то второй параметр μ является характеристикой «комбинаторного наращения» [2; 5]. Этот подход можно и нужно использовать не только для новой и старой технологии (новая и старая комбинация по Й. Шумпетеру), но и для разделения совокупных инвестиций на инвестиции в человека (человеческий капитал) и фонды (постоянные и переменные – основной и оборотный капитал), с получением соотношений согласно закону изменения скоростей создаваемого и отвлекаемого ресурса в каждое направление инвестирования.

Если ввести, что инвестиции в новые комбинации состоят из ресурса R 1 = α I s , R 2 = μ I n , то есть доли отвлекаемых инвестиций от старых комбинаций I s и вновь создаваемого ресурса R 2 как доли от инвестиций в новые комбинации – I n , то инвестиции (I n ) определяются как сумма R 1 и R 2 . Или I n = αI s + μI n (I = I n +I s ). Откуда

dI„    a dL   I d a I a   d a

- =         - +   -      + s 2    , dt 1 — у dt 1 — у dt (1 — у) dt

= da a = ~dt ’ v = da у dt ’

X =

^{1 —} a’

dI       dI

ЗГ = ^aX ,s + I - X V a + I - ^aX ^V у . dt       dt

I

n

a

1 — у.

^Is ^.

Если доля отвлекаемых ресурсов от старой комбинации и вновь создаваемого ресурса изменяется, тогда исходя из (1)

можно записать, что

Эмпирически получив законы изме-

нения параметров α, μ, а также получив закон изменения инвестиций в старые комбинации (технологии), несложно вывести изменение инвестиций в новые комбинации

при данном законе изменения скорости отвлечения ресурса (V α ) и создания (V μ ) нового ресурса и изменении соответственно долей этих ресурсов – α, μ.

Известно, что динамика валового внутреннего продукта зависит от инвестиций, однако вклад в эту динамику инвестиций в новые и старые комбинации по Й. Шумпетеру будет также различаться [2].

Далее покажем, каким образом можно использовать развитие теоретических положений неошумпетерианской теории к решению задач обоснования промышленной политики. Неошумпетерианская теория позволяет применить к исследованию изменений в промышленности синтез структурноинституционального и ресурсно-факторного подходов, которые составляют, по мнению авторов, полезный инструментарий верификации направлений стратегического развития экономической системы, в частности промышленности.

Анализ структуры «старые/ новые» технологии промышленности России

В рамках современной неошум-петерианской теории индустриального развития в силу возникновения новых комбинаций в зависимости от соотношения базовых и новых технологий происходит изменение структуры экономики и задаётся общий темп ее роста [5]. Существенное, если не определяющее, значение в области технологического развития экономической системы отводится заня-

тому персоналу, который является носителем «технологического знания» (и обеспечивает наращение данного вида знания в виде технической и др. документации). В связи с этим изменение структуры «старые /новые» технологии удобно рассмотреть, исследуя вопрос о переливе трудового ресурса между экономическими секторами, в данном случае между секторами промышленности.

Допустим, что в момент времени t1 общее число занятых в экономическом секторе составляет Lt1, число занятых с использованием «новых» технологий составляет Lnt1, с использованием «старых» – Lst1. Соответственно в момент времени t2 величины будут равны Lt2, Lnt2 и Lst2. Общее изменение численности в экономическом секторе составит ΔL=Lt2 – Lt1, причем данная величина будет складываться из двух составляющих. Первая часть – это агенты, которые по тем или иным причинам не занимаются больше трудовой деятельностью в промышленности (стали безработными или перешли на работу в совершенно другую сферу деятельности, например банковскую), а вторая часть – перешедшие на работу из рассматриваемого сектора в другой либо пришедшие в этот сектор. Эти два потока образуют так называемый «отток» и «приток» занятых в экономическом секторе. Кроме того, в момент времени t1 число занятых в производстве на новых и старых технологиях соответственно L1n, L1s в момент t2 будет L2n, L2s, так что общее число занятых для начального и следующего момента времени составит L1 = = L1n + L1s, L2 = L2n + L2s. Если приток занятых в экономический сектор равен l = ln +ls и распределяется в виде работающих на «новых» (ln) и «старых» (ls) технологиях, тогда за период времени [t1, t2] к моменту t2 число занятых в производстве на «новых» технологиях будет равно L2n = L1n + lsn +ln, то есть исходному числу занятых в этом же производстве L1n плюс те агенты, которые будут отвлечены от производства на старых технологиях (lsn), плюс те агенты, которые вновь приняты сразу на производство на новых технологиях (ln). Конечно, к моменту t2 возможен сценарий, когда агенты отвлекаются не из производства на старых техноло- гиях и переходят на виды производств на новые технологии (обучаясь и повышая квалификацию), а, наоборот, когда кадры из производства на новых технологиях переходят в производство на старых технологиях, тогда параметр lsn входит в выражение для L2n со знаком «минус». Выражение для занятых в производстве на старых технологиях примет вид L2s = L1s+ ls – lsn. В случае когда кадры переходят из производств на новых технологиях в производства на старых технологиях, параметр lsn в выражение для L2s войдёт со знаком «плюс». Таким образом, подводя итог приведенным рассуждениям, можно записать следующие уравнения:

• 1)    L 2 _n = L 1 _n + l _sn +l _n , L 2 _s = L 1 _s + l _s – l _sn ; (3)

• 2)    L 2 _n = L 1 _n – l _sn +l _n , L 2 _s = L 1 _s + l _s + l _sn .

Тогда параметры α и μ, характеризующие соответственно отвлечение ресурса от производств на старых технологиях и создание (привлечение) нового ресурса – под производства на новых технологиях, определятся для рассматриваемого интервала времени так: α = l sn / L 1s , µ = l n / L 2n . Скорости отвлечения и создания ресурса, характеризующие соответственно «созидательное разрушение» и «комбинаторное наращение», будут равны V α = dα/dt и V μ = dμ/dt соответственно (см. формулу (2)).

Аналогичные рассуждения справедливы и вполне применимы не только к фактору «труд», но и «капитал». В данной статье ограничимся расчётами и оценками только по фактору «труд». При этом заметим, что подобный анализ важен по всем факторам производства. В рамках использования аппарата производственных функций возможно дополнительное моделирование факторных связей. Особый интерес представляет исследование технологического замещения, то есть эффекта, когда новые технологии вытесняют старые («эффект замещения»), а также случая, когда они дополняют старые технологии («эффект дополнения»), сохраняя их в виде необходимого технологического звена производства, или, как вариант, включают старые технологии в качестве своего элемента («эффект включения»). Учитывая, что в российской экономике в период 2008–2014 гг. наблюдалось некоторое снижение общего технологического уровня [2; 5] при росте числа передовых технологий и сокращении числа уже используемых технологий, можно утверждать, что технологического замещения в прямом смысле не наблюдалось, хотя «эффект дополнения» и «эффект включения» имманентно присутствовали.

Примем величину затрат на технологические инновации в качестве затрат на новые технологии I n (t), а общую величину затрат в основной капитал – в качестве всех инвестиций I(t). Тогда разницу между величиной всех инвестиций в основной капитал и затратами на технологические инновации в виде затрат на старые технологии, обозначенные I s (t), на примере производства машин и оборудования, электрооборудования, электронного и оптического оборудования, транспортных средств и оборудования в России рассчитаем в табл. 1 ¹ .

Таблица 1

Величина инвестиций в производство машин и оборудования, электронного и оптического оборудования, электрооборудования, транспортных средств и оборудования в РФ, 2009–2014 гг.*

Год	Показатель
	s “ = sl-J® я s О	ШЙ Й S g a & « » § а Й я g § S а s inh й □ ч g ь	i i 4 а HHi » а й й й й § !Ш5 J е s ©
2009	183448,3	46672,3	136776
2010	201346,1	45411,4	155935
2011	204759,9	58445,8	146314
2012	276894,2	79634,3	197260
2013	349706,2	120050,5	229656
2014	392302,8	137305,9	254997

* Рассчитано авторами по источнику: Федеральная служба государственной статистики. URL: statistics/science_and_innovations/science/# (дата обращения: 01.02.2017).

Как видим, общая величина инвестиций в сектор растет. В свою очередь, увеличиваются как инвестиции в технологические инновации в абсолютном выражении, так и их доля в структуре инвестиций. За период 2009–2014 гг. величина инвестиций в «новые» технологии возросла в 2,9 раза, а в «старые» – в 1,8 раз без учета инфляции, что объясняется политикой поощрения инновационной деятельности предприятий.

В настоящем исследовании численность занятых в разработках принята в качестве численности занятых в «новых» технологиях L n (t). Соответственно разница между величиной всех занятых и занятых в разработках есть численность работающих на «старых» технологиях L s (t).

Далее проведём анализ изменений структуры «старые/новые» технологии по численности занятых в производстве на новых и старых технологиях.

Общая численность занятых в промышленности России за 2005–2014 гг., а также в регионах Центрального федерального округа ежегодно уменьшается (табл. 2). Численность занятых в новых и старых производствах также сокращается (табл. 3 и 4). При этом доля персонала, занятого исследованиями и разработками, несколько возрастает (табл. 5) ² .

Таблица 2

Численность занятых в промышленности, чел.

Год	Макрорегион
	Российская Федерация	Центральный федеральный округ
2005	14675200	3816200
2010	13255200	3428600
2011	13283000	3419100
2012	13196800	3384500
2013	13075400	3343300
2014	12848800	3305400

Таблица 3

Численность занятых в «новых» производствах, чел.

Год	Макрорегион
	Российская Федерация	Центральный федеральный округ
2005	813207	408330
2010	736540	381795
2011	735273	380363
2012	726318	373461
2013	727029	375087
2014	732274	381047

Таблица 4

Численность занятых в «старых» производствах, чел.

Год	Макрорегион
	Российская Федерация	Центральный федеральный округ
2005	13861993	3407870
2010	12518660	3046805
2011	12547727	3038737
2012	12470482	3011039
2013	12348371	2968213
2014	12116526	2924353

Таблица 5

Доля занятых в разработках в промышленности, %

Год	Макрорегион
	Российская Федерация	Центральный федеральный округ
2005	5,54	10,70
2010	5,56	11,14
2011	5,54	11,12
2012	5,50	11,03
2013	5,56	11,22
2014	5,70	11,53

Проведем дальнейшие оценки изменения числа занятых по секторам промышленности Российской Федерации3. Для упрощения расчётов выделим шесть базисных секторов российской промышленности согласно Общероссийскому классификатору видов экономической деятельности (ОКВЭД) (табл. 6).

Основываясь на статистических источниках по России 4 , дадим общую характеристику динамики численности занятых в производстве с использованием новых технологий в выделенных в табл. 6 секторах промышленности.

В первом секторе (добывающая промышленность) с 2003 по 2007 гг. произошёл двукратный рост занятых в производстве с использованием новых технологий, к 2011 г. (составил 10 тыс. человек) этот показатель вернулся к уровню 2003 г. и до 2014 г. возрос с 5 до 7 тысяч занятых.

По второму сектору число занятых составляло не более 1000 человек, причём в период 2010–2014 гг. это число сокращалось до 400 человек, затем вновь увеличивалось до 1000 человек и затем (2014 г.) опять снизилось до 600 человек.

В третьем секторе объём занятых не превышал 400 человек, причём общий тренд был понижательный на всём периоде вплоть до 100 человек.

Четвёртый сектор показал динамику неуклонного снижения числа занятых в производстве на новых технологиях примерно с 15 до 10 тыс. человек за период 2003–2014 гг.

Пятый сектор обеспечивает наибольшую занятость в общей структуре занятых в промышленности, работающей на новых технологиях – более 50 тыс. человек. Причём к 2009 г. снижение достигло почти 40 тыс. человек, к 2014 г. произошло восстановление числа занятых в этом секторе экономики.

Шестой сектор демонстрировал наименьшую занятость в кризисные 2008– 2009 гг., а также в 2010 г. – порядка 100 человек, с увеличением этого числа до 700 занятых в 2014 г.

Таблица 6

Секторы промышленной системы и соответствующие им виды экономической деятельности [6]*

Обозначение сектора промышленности	Код ОКВЭД	Расшифровка ОКВЭД
1	CA	Добыча топливно-энергетических полезных ископаемых
	CB	Добыча полезных ископаемых, кроме топливно-энергетических
	DF	Производство кокса, нефтепродуктов и ядерных материалов
2	DA	Производство пищевых продуктов, включая напитки, и табака
	DB	Текстильное и швейное производство
	DC	Производство кожи, изделий из кожи и производство обуви
3	DD	Обработка древесины и производство изделий из дерева
	DE	Целлюлозно-бумажное производство; издательская и полиграфическая деятельность
4	DG	Химическое производство
	DH	Производство резиновых и пластмассовых изделий
	DI	Производство прочих неметаллических минеральных продуктов
	DJ	Металлургическое производство и производство готовых металлических изделий
5	DK	Производство машин и оборудования
	DL	Производство электрооборудования, электронного и оптического оборудования
	DM	Производство транспортных средств и оборудования
6	E	Производство и распределение электроэнергии, газа и воды

* Далее в статье для обозначения секторов промышленности будут использоваться введенные в таблице обозначения.

Далее рассчитаем массу структурного сдвига по занятым в «новых» производствах (табл. 7).

Таблица 7

Масса структурного сдвига по занятым в «новых» производствах в 2004–2014 гг., %

Год	Сектор промышленности
	1	2	3	4	5	6
2004	0,67	0,27	–0,04	–1,32	0,08	0,34
2005	–0,26	–0,21	–0,09	1,71	–1,14	0,00
2006	2,38	–0,01	–0,10	–2,01	–0,47	0,20
2007	3,32	0,02	0,11	–1,23	–1,71	–0,52
2008	–3,25	0,26	–0,06	–0,56	3,50	0,11
2009	0,00	0,00	0,00	0,00	0,00	0,00
2010	–0,26	0,53	–0,03	–1,27	1,60	0,03
2011	–1,09	–0,94	–0,03	0,20	1,83	0,26
2012	0,67	1,00	0,00	–0,72	–2,09	0,30
2013	0,14	–0,82	0,41	–2,43	2,65	0,05
2014	0,96	0,14	–0,46	–1,26	0,89	–0,27

Суммарная масса структурного сдвига в период 2003–2014 гг. показывает следующие изменения в структуре занятости в промышленности. Максимально выросла доля занятых в новых производствах в секторе «5», масса структурного сдвига равна

• 5 ,14. Минимальная величина суммы массы структурного сдвига, составляющая –8,88%, приходится на сектор «4», что указывает на постепенное уменьшение доли занятых в «новых» производствах в данном секторе. Возрастает доля занятых в «новых» производствах также в секторах «1», «2» и «3». Помимо сектора «4» отрицательную величину структурного сдвига, равную –0,27, показывает сектор «3». Тем самым можно утверждать, что развитие новых технологий и новых видов производств по разным видам деятельности – секторам промышленности происходило явно неравномерно. Более того, одни секторы развивались, условно говоря, за счёт других секторов, включая перемещение кадров между ними [2].

Так, за счет уменьшения доли занятых в «новых» производствах в химической и деревообрабатывающей промышленности происходит значительный рост доли занятых в «новых» производствах во всех остальных секторах промышленности. В табл. 8 приведены данные по числу «старых» и новых технологий по секторам промышленности.

Таблица 8

Число технологий по секторам промышленности в 2010–2015 гг.*

Сектор промышленности	Число «новых» технологий, шт.						Число «старых» технологий, шт.
	^4 о гч	^4 14 о гч	гч 14 о гч	со ^4 гч	^4 гч	in ^4 гч	^4 гч	^4 ^4 гч	^4 гч	СП ^4 гч	^4 гч	^4 сч
1	5	10	14	15	25	18	7914	8474	9527	9050	8892	9222
2	10	16	32	20	23	19	14081	13633	14045	14513	15256	17099
3	0	16	9	15	14	22	11755	12404	12346	14029	14751	15603
4	45	91	91	119	123	122	26097	26399	27150	29135	30962	33207
5	155	164	162	213	221	237	68456	53411	55472	54879	56992	66829
6	6	23	32	38	33	28	16262	14649	14237	15959	16971	18443
Всего	221	320	340	420	439	446	144565	128970	132777	137565	143824	160403

* Рассчитано авторами по источнику: Федеральная служба государственной статистики. URL: (дата обращения: 01.02.2017).

Анализируя полученные данные, заключим, что в период 2010–2015 гг. происходил рост числа новых технологий и сокращение числа «старых». При этом с 2015 г. общее число традиционных технологий начинает возрастать. Интересно отметить, что это год рецессии – абсолютного спада ВВП на 3,7% и спада промышленного производства, при том что прирост новых технологий крайне незначительный. При этом прирост традиционных (используя наш термин «старых») технологий в 2015 г. оказался весьма существенным. Заметим, что рост экономической системы зависит не только от параметра α, но и от величины показателя µ. Поэтому потеря значительного числа «старых» технологий в промышленности может приводить только к несбалансированному росту общего объема производства по секторам экономики. Возобновление этих технологий, например в условиях рецессии, создаёт прочную основу для организации промышленного подъёма на следующих этапах развития системы при соответствующей стимулирующей экономической политике. Отмеченные выше структурные изменения в секторах промышленности выступают своеобразным правилом, определяющим дальнейший перелив ресурсов между ними.

Определение параметров α и μ для промышленного предприятия

В силу того что данные, необходимые для анализа изменения скоростей перелива ресурсов

Vα и Vμ (по параметрам – α и μ), в рамках общероссийского статистического учёта не собираются, покажем возможность применения предлагаемой структурной модели на конкретном промышленном предприятии. Это и составит демонстрацию следствий из развиваемой неошумпетерианской теории применительно к объекту промышленности.

В качестве такого предприятия выбрано АО «Карачевский завод “Электродеталь”». Предприятие является ведущим разработчиком и производителем прямоугольных электрических соединителей, используемых в энергетике, судостроении, космосе, на железной дороге, в радиоэлектронных системах, авиации и др. отраслях 5 . При разработке продукции применяются как традиционные (старые), так и новые технологии, что является главным условием для демонстрации модели.

Проанализируем перелив ресурсов по данному предприятию. В табл. 9 приведены исходные данные. Рассчитанные параметры α и μ (рис. 1–2) оценивались по занятому персоналу, который отвлекается от прежней работы и принимается на новую работу, что и символизирует принцип «созидательного разрушения», когда ресурс отвлекается от прежних возможностей использования и влекается либо создаётся новый ресурс в ви-«комбинаторного наращения», когда при-      де новых работников.

Таблица 9

Показатели деятельности АО «Карачевский завод “Электродеталь”»*

№	Наименование показателя	2011	2012	2013	2014	2015
1	Затраты на технологические инновации, тыс. руб.	3770,9	25619,9	20451,0	28453,8	218883,7
2	Инвестиции в основной капитал, тыс. руб.	15800	138552	87994	357244	496787
3	Численность работающих, чел.	1385	1406	1386	1449	1540
4	Численность занятых в подразделениях, осуществляющих технологические инновации, чел.	51	55	94	118	115
5	Численность перешедших в подразделения, осуществляющие технологические инновации, из других подразделений, чел.	1	2	2	1	1
6	Среднегодовая стоимость основных фондов, тыс. руб.	605680	701518	824401	859028	1214063
7	Среднегодовая стоимость основных фондов, используемых в производстве с применением технологических инноваций, тыс. руб.	30740	98285,814	82189,457	195776,434	278006,276
8	Объем выпущенной продукции, тыс. руб.	500777	803689	1040397	1477992	1896077
9	Объем выпущенной продукции с технологическими инновациями, тыс. руб.	27354	1868,25	95781	66989,3	319847,8
10	Число используемых производственных технологий, шт.	350–400	350–400	350–400	350–400	350–400
11	Число инновационных (новых) технологий, шт.		99	136	126	150
12	Объем отгруженных товаров собственного производства, выполненных собственными силами работ и услуг в действующих ценах, тыс. руб.	456698	746235	1067394	1375734	1750626
13	Средняя заработная плата, руб.	12174	14600	18260	23386	25115

* Данные предоставлены руководством АО «Карачевский завод “ Электродеталь ” ».

0,0018

0,0016

0,0014

0,0012

0,001

0,0008

0,0006

y = 0,0001x3 - 0,0012x2 + 0,0037x - 0,0019

0,99

0,98

0,97

0,96

y = -0,0037x3 + 0,0358x2 - 0,0965x + 1,0444 R² = 0,9851

0,0004

0,0002

J α

2012    2013    2014    2015

Полиномиальная (α)

0,95

0,94

2011    2012    2013    2014    2015

—^ µ         Полиномиальная (µ)

Рис. 1. Параметр α (по отвлечённым занятым) в 2011–2015 гг.

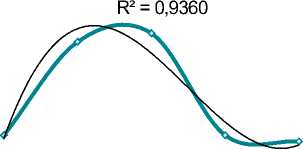
Рис. 2. Параметр µ (по привлечённым занятым) в 2011–2015 гг.

Наглядно видно, что на предприятии параметр α, характеризующий скорость перехода людей из «старых» производств в «новые», оказывается очень низким, а увеличение числа занятых в новых производствах происходит за счет прихода на предприятие людей, ранее там не работавших. Таким образом, можно охарактеризовать данную ситуацию как «комбинаторное наращение» 6 , при которой новые комбинации не возникают из старых, отвлекая ресурс, а создаются вновь за счёт нового для системы ресурса.

Построенные на рис. 1 и 2 зависимости принимают вид

α = 0,0001t3 – 0,0012t2 + 0,0037t – 0,0019 (R² = 0,936);

µ = –0,003t³ + 0,035t² – 0,096t + 1,044 (R² = 0,985) 7 ;

V α = dα / dt = 0,0003t² – 0,0024t + 0,0037;

V µ = dµ / dt = –0,009t² + 0,070t – 0,096.

На рис. 3 представим скорости перелива ресурса, характеризующие силу действия принципа «созидательного разрушения» или «комбинаторного наращения».

0,05

0,04

0,03

0,02

> 0,01

£ 0

-0,01

-0,02

-0,03

-0,04

«комбинаторное наращение» z * *

«созидательное / разрушение» J

2011   /2012    2013    2014    2015

/

/

/

t

^^^^^^^^M Vα             Vµ

Рис. 3. Скорости перелива ресурсов на промышленном предприятии

Как видно из рис. 3, до 2012 г. развитие предприятия «Карачевский завод “Электродеталь”» обеспечивалось на основе принципа «созидательного разрушения», то есть за счёт имеющихся ресурсов, затем произошло изменение режима развития, стал доминировать принцип «комбинаторного наращения». Причиной является как расширение списка задач развития данного предприятия, так и насыщение в использовании трудового фактора, включая и выбытие персонала до 2013 г., а также снижение уровня компетенций и др.

На наш взгляд, представляет интерес анализ потенциальных возможностей предприятия в случае изменения коэффициентов α и µ. Рассмотрим, как изменялась бы величина продукции, выпущенной предприятием, если бы величина перелива ресурсов по параметрам α и µ принимала другие значения.

Построенные регрессионные зависимости величины «новой» и «старой» продукции от величины занятых в «новых» и «старых» производствах имеют вид Qn = 2641 Ln – 12634;

Qs = 78,62 Ls² – 20933 Ls 8 .

Построив регрессии по эмпирическим значениям числа занятых в производстве «старой» и «новой» продукции от времени, получим

Ln = –2,071t² + 31,52t + 14,8, Ls = 18t² – 91,8t + 1424 9 .

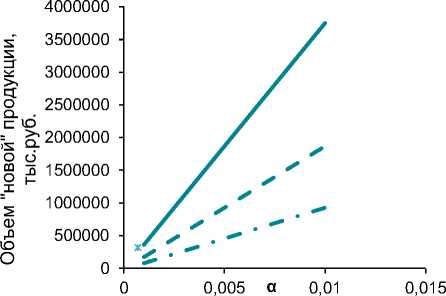
Зададим возможные значения α и µ и рассчитаем значения Ln, а затем и потенциально возможный при заданных условиях объем продукции. Поскольку параметр α является более поддающимся управлению на предприятии за счет переподготовки имеющихся сотрудников и перевода их из «старых» в «новые» производства (иногда даже без переподготовки), будем считать, что теоретически возможной является величина α, находящаяся в интервале от 0 до 0,01 (судя по эмпирическим значениям α за рассматриваемый период). Используем три варианта значений показателя µ – среднее за период 2011–2015 гг., максимальное и минимальное за тот же период. Нанесем точки, показывающие значения «новой»10 продукции при различных вариантах α и µ, а также реальное значение объема производства при фактических значениях α и µ в 2015 г. (рис. 4).

µ=0,96                   µ=0,99

µ=0,98                 Qn факт

Рис. 4. Потенциально (теоретически) возможный объем производства новой продукции при разных комбинациях α и µ

Таким образом, согласно рис. 4, чем большее значение принимает величина показателя µ, тем больше воздействует на рост объема новой продукции рост величины показателя α.

На практике (в отличие от теоретических оценок) достижение такого значения объема «новой» продукции не представляется возможным и необходимым. Для реального значения параметра μ рассматриваемого предприятия значение α фактически задаёт параметры возможного обучения, переобучения (так как характеризует перелив кадров от старых к новым технологиям). Следовательно, переобучение должны проходить примерно 50–100 человек в разные годы рассматриваемого интервала времени. Повышение величины α до 0,007, т.е. переобучение 10 человек для перевода из «старых» в «новые» производства, вызывает рост объема продукции примерно на 15% в период 2011–2015 гг. с постепенным уменьшением величины превышения. Переобучение 10 человек (α=0,007), 20 (α=0,015) или 30 человек (α=0,0225) приведёт в среднем к увеличению объёма производства на 17%, 20% и 28%. Перевод уже имеющихся сотрудников с производства «старой» про- дукции на «новую» оказывает существенное влияние на изменение общего объема производства. Поэтому у данного предприятия имеются резервы для нара- щивания нового производства на основе новой технологии (которой обязательно необходимо обучать людей). Заметим, что затраты на обучение включаются в стоимость продукции и учтены в параметрах регрессии посредством величин Ls, Ln.

Однако необходимо принимать управленческие решения, не только направленные на освоение новых видов продукции, внедрение в производство передовых технологий, но и на поддержание «старых» базовых технологий и производств, потеря которых грозит про- мышленности возникновением ситуации, при которой внедрение новых технологий станет невозможным ввиду отсутствия базовых технологий, особенно при условии, когда не действует эффект «технологического замещения».

Это может привести к тому, что для повышения технологичности пред- приятию придется привлекать ресурсы требуемого качества (квалификации) из других источников, в том числе из-за рубежа, что повысит как издержки производства, так и импортную зависимость отечественной промышленности, снизит уровень национальной безопасности страны. Поэтому решение задачи обоснованного перераспределения имеющегося ресурса с учетом привлечения ресурса из отечественных секторов различного назначения составляет стратегическую задачу промышленно-структурной политики России.

Выбор стратегических решений для развития промышленной системы (методическое обеспечение)

Представим структуру промышленной системы, состоящей в общем виде из двух основных частей – обрабатывающей и добывающей. При этом к обрабатывающим можно отнести выделенные ранее секторы «2», «3», «5», а к добывающим – «1», «4», «6».

Согласно теории реструктуризации и индустриального развития [5] изменение доли каждого сектора зависит от изменения капитала, труда, технологий и правительственных воздействий (вводимых институтов), и от функционирования других секторов экономики. Изменение каждого фактора, в свою очередь, зависит от набора институциональных параметров системы. Проведя регрессионный анализ и установив регрессионные зависимости по эмпирическим данным рассматриваемой промышленной системы, можно определить факторы и степень их воздействия на результирующий показатель (величину доли сектора в системе), проектировать управленческие воздействия в рамках осуществления промышленной политики, влияя на перелив ресурсов между секторами и на структуру экономики.

В силу того что не все показатели можно определить с помощью данных Федеральной службы государственной статистики, примем следующие показатели в качестве факторов: изменение величины труда и капитала за год (dL/dt и dK/dt); изменение технологического уровня (dT/dt); институты промышленного развития как величина финансирования в рамках государственных программ развития промышленности (dI/dt), который оценивался как относительное изменение расходов на Федеральные целевые программы и госпрограммы, воздействующие на сектор «5» с лагом в 3 года) 11 . Изменение объёма выпуска обозначим как dQ/dt.

Для построения регрессий использованы данные для сектора «5» за период 2006–2015 гг. (табл. 10).

Таблица 10

Исходные данные для построения уравнения регрессии по сектору «5»*

Год	Показатель
	dQ/dt	dL/dt	dK/dt	dT/dt	dI/dt
2006	0,210	–0,450	–0,710	–0,0207	0,0421
2007	1,040	–0,020	–0,400	0,0159	0,0571
2008	–0,260	0,300	–0,250	0,0242	0,3964
2009	–1,740	–1,030	–0,640	–0,099	1,5825
2010	1,130	–0,840	–0,160	0,0186	1,0400
2011	0,720	0,460	–0,500	0,0037	0,2464
2012	0,660	0,140	–0,070	–0,007	0,2022
2013	0,010	–0,140	–0,240	–0,013	0,0577
2014	–0,710	–0,150	–0,510	–0,003	0,1328
2015	–1,500	–0,240	–0,220	–0,0134	0,1755

* Таблица составлена по данным табл. 6.

Полученное уравнение регрессии имеет вид dQ/dt = –0,14 – 0,13 dL/dt –0,55 dK/dt + + 24,57 dT/dt +0,24 dI/dt.

Матрица парных коэффициентов корреляции, построенная для выявления мультиколлинеарности и возможного исключения факторов из анализа, приведена в табл. 11. Поскольку |r dL/dt, dI/dt |> 0,7, то существует возможность мультиколлинеарности факторов dL/dt и dI/dt и необходимость исключения одного из них из анализа.

Таблица 11

Матрица парных коэффициентов корреляции для функции со всеми факторами

Показатель	dQ/dt	dL/dt	dK/dt	dT/dt	dI/dt
dQ/dt	1	0,338	0,284	0,68	–0,32
dL/dt	0,338	1	0,264	0,611	–0,718
dK/dt	0,284	0,264	1	0,51	–0,135
dT/dt	0,68	0,611	0,51	1	–0,59
dI/dt	–0,32	–0,718	–0,14	–0,59	1

В случае исключения фактора dI/dt (отказ от госпрограмм) уравнение регрессии имеет вид dQ/dt = –0,0428 – 0,28 dL/dt – 0,44 dK/dt + + 23,36 dT/dt.

В случае исключения фактора dL/dt (не изменения фактора «труд») уравнение регрессии имеет вид dQ/dt = –0,15 – 0,57 dK/dt + 24,12 dT/dt + + 0,31 dI/dt.

Построим различные варианты регрессии совокупного выпуска в промышленности в исследуемый период (рис. 5).

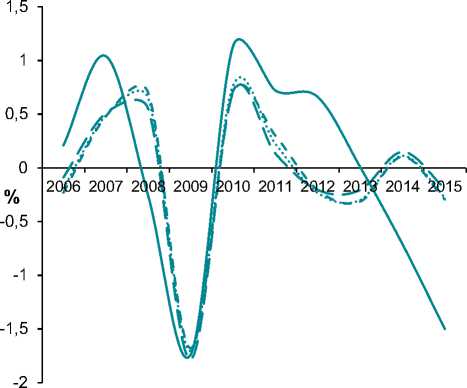
dQ/dt эмпирическое dQ/dt с 4 факторами dQ/dt в случае исключения фактора 4

dQ/dt в случае исключения фактора 1

Рис. 5. Эмпирические и регрессионные функции dQ/dt

Матрицы парных коэффициентов корреляции для функций с исключенными факторами dI/dt и dL/dt приведены в табл. 12 и 13 соответственно.

Таблица 12

Матрица парных коэффициентов корреляции для функции с исключенным фактором dI/dt

Показатель	dQ/dt	dL/dt	dK/dt	dT/dt
dQ/dt	1	0,338	0,284	0,68
dL/dt	0,338	1	0,264	0,611
dK/dt	0,284	0,264	1	0,51
dT/dt	0,68	0,611	0,51	1

Таблица 13

Матрица парных коэффициентов корреляции R для функции с исключенным фактором dL/dt

Показатель	dQ/dt	dK/dt	dT/dt	dI/dt
dQ/dt	1	0,284	0,68	–0,32
dK/dt	0,284	1	0,51	–0,135
dT/dt	0,68	0.51	1	–0,59
dI/dt	–0,32	–0.135	–0,59	1

В табл. 12 и 13 нет значений парных коэффициентов корреляции, превышающих по модулю 1, следовательно, факторы в этих двух функциях не являются мульти-коллинеарными.

Однако в случае если в уравнение регрессии входят все факторы, коэффициент множественной корреляции равен 0,695, а коэффициент детерминации составляет 0,483.

В случае исключения фактора dI/dt коэффициент множественной корреляции равен 0,691, коэффициент детерминации – 0,477.

В свою очередь, исключение фактора dL/dt даст коэффициент множественной корреляции 0,694 и коэффициент детерминации 0,481.

Таким образом, наиболее точно описывает поведение функции dQ/dt уравнение функции, включающей в себя 4 фактора.

Для определения степени влияния факторов на результативный признак dQ/dt были определены частные коэффициенты эластичности (табл. 14).

Таблица 14

Частные коэффициенты эластичности

Фактор	Модель со всеми факторами	Модель без фактора dL/dt	Модель без фактора dI/dt
dL/dt	–0,6		–1,24
dK/dt	–4,6	–4,78	–3,7
dT/dt	5,23	5,13	4,97
dI/dt	–2,12	–2,74	–

Поскольку в табл. 14 в модели со всеми факторами частные коэффициенты эластичности факторов последних трех факторов по модулю больше 1, следовательно, их влияние на результирующий показатель существенно. Показатель dL/dt имеет величину частного коэффициента эластичности, равного –0,6, поэтому его влияние незначительно. Иными словами, за счёт фактора «труд» в промышленности невозможно поднять производительность. В моделях без факторов dL/dt и dI/dt частные коэффициенты эластичности всех факторов по модулю больше 1, значит, факторные признаки существенно влияют на результирующий показатель.

Итак, как показал наш анализ, максимальное воздействие на изменение в секторе машиностроения имеет фактор dT/dt, затем – фактор dK/dt, на третьем месте – фактор dI/dt, минимальное воздействие ока- зывает фактор dL/dt. Соответственно указанным приоритетам необходимо проектировать управленческие решения. Иными словами, возможна некая иерархия в видах воздействия на динамику развития промышленности, что не может не учитываться при разработке промышленной политики, проектируемой на научно обоснованной основе. Конечно, фактор «труд» привязан к технологическому изменению развития машиностроения и промышленности в целом, поэтому его влияние оказывается по модели малым – речь идёт лишь об определении первичности воздействий. Действительно, в области труда и трудовых отношений быстрые и кардинальные изменения вряд ли возможны, что и подтверждают модельные построения для сектора промышленности (машиностроение). Теперь важно разобраться с набором общих действий в рамках экономической политики, влияющей на развитие промышленности. Эти действия также нужно разделить по управленческим воздействиям на капитал, труд, технологии и институты. Заметим, что другие направления экономической политики и институциональные коррекции так или иначе влияют на развитие промышленности, и увязка этих мер, совместное их действие, а также раздельное влияние на релевантные факторы требует дополнительного изучения и является в общем смысле нетривиальной задачей.

Для сектора «5», который обобщённо представлен здесь как «машиностроение», основные усилия экономической политики должны быть в первую очередь направлены на повышение его технологического уровня.

Следующие по уровню значимости мероприятия должны быть направлены на улучшение состояния используемого капитала (основные фонды). Реализация мероприятий, направленных на капитал (основные фонды) промышленного сектора, должна привести к изменению его рентабельности, величины удельного продукта по капиталу и уменьшению износа, что внесёт серьёзный вклад в повышение общей технологичности экономической системы.

Улучшение степени воздействия институтов на развитие машиностроения, а также соблюдение необходимой частоты институциональных изменений в данном секторе экономики 12 создаст стабильные условия для реализации последующих мер промышленной политики.

Влияние фактора «труд» может быть изменено посредством роста величины заработной платы вне связи с производительностью труда, так как производительность будет повышаться за счёт факторов «капитал» и «технологии», а также институтов развития.

Поэтому связь «заработная плата – производительность», которая не является жёсткой для России, не следует использовать на этапе активной политики структурных изменений и промышленной политики. Стратегической целью является не производительность факторов производства как таковая, а структура промышленного производства (технологическая, инвестиций, продукции, кадров, рынков), управление переливом ресурсов (кадров) и соразмерное технологическое переоснащение производств. В государственном секторе это потребует коррекции программ развития промышленности, в частном – создания специальных институтов, поощряющих такой формат развития. В рамках региональных экономических систем, особенно промышленных регионов, в качестве теоретического ядра формирования новой промышленной политики может использоваться концепция институтов саморазвития и согласованного развития подобных систем [2; 3; 4; 6].

Заключение

Р ассмотрев неошумпетериан-ский взгляд (теорию) на формирование промышленной политики, мы можем сделать несколько релевантных выводов.

• ¹²    С одной стороны, институциональные изменения должны позитивно сказываться на параметрах функционирования промышленной системы, но с другой – проведение слишком частых изменений не дает возможности агентам адекватно приспособиться к изменениям.

Во-первых, наравне с принципом «созидательного разрушения», символизирующим в общем «распределительную» логику развития, проявляется принцип «комбинаторного наращения», когда сочетание различных технологий даёт новые технологические решения, определяя для них и новый ресурс, причём само это сочетание не требует дополнительного объёма ресурса и даже не отвлекает значительного ресурса от традиционных технологических возможностей. Распределение ресурса в рамках этих двух эффектов хорошо демонстрируется на примере решения структурной задачи распределения инвестиций между новыми и старыми технологиями.

Во-вторых, исследование механизма «созидательного разрушения» и «комбинаторного наращения» возможно посредством анализа динамики числа занятых в производстве с использованием новых и старых технологий. При этом параметры скорости перелива определяют режим функционирования промышленного объекта. Развитие выбранного для демонстрации модели промышленного предприятия происходит не за счёт отвлечения трудового ресурса из области занятости в производстве на основе старых технологий, переориентации на новые технологии, а за счёт привлечения новых кадров для работы на производстве, оснащенном новыми технологиями. Вместе с тем можно перспективно оценить, насколько возможно привлекать этот новый ресурс и каким образом подготовка, обучение уже занятого персонала с переводом его в производство на новых технологиях скажется на объёме выпуска и финансово-экономических показателях функционирования предприятия.

В-третьих, проведенный регрессионный и факторный анализ на примере сектора машиностроения позволил установить, что прирост объема выпуска зависит от основных условий развития промышленности (капитал, труд, технологии, ин-ституты13) с определяющей значимостью технологий. Именно этот фактор оказывает наиболее сильное влияние на показатель совокупной производительности в промышленности. В связи с этим сдерживание роста заработной платы при недостаточном росте производительности не является обоснованным мероприятием экономической политики. Общий уровень технологичности промышленности будет влиять на этот параметр сильнее, так как недостаточность ресурса по старым технологиям может существенно затормозить развитие. Конечно, исследование этой проблемы должно быть продолжено и углублено, так как необходимо учитывать эффекты технологического «замещения», «дополнения» и «включения». Предложенное авторами статьи методическое обоснование стратегических решений, связанных с выбором необходимых для развития промышленного сектора факторов производства и выбором режима управления переливом ресурсов по занятому в секторе персоналу, связанному с освоением новых или сохранением традиционных технологий, является основанием для проведения последующих исследований.

В целом результаты исследования позволяют сделать вывод, что повышение уровня технологичности российской экономики возможно за счёт наращения результатов в области используемых (старых) и применения новых технологий [7]. Однако за рассматриваемый интервал времени число используемых передовых производственных технологий снизилось на четверть. В обрабатывающих отраслях промышленности наблюдается общая потеря передовых технологий при росте числа разработанных передовых технологий. Следовательно, центральной задачей является повышение общей технологичности экономической системы России с общим вектором на целесообразное распределение инвестиций между старыми и новыми технологическими возможностями. Это принципиально уточняет тот алгоритм формирования приоритетов национального развития, которому следуют российские органы власти в настоящее время.

Посвящаем эту публикацию памяти академика РАН, директора Уральского отделения ФГБУН «Института экономики Российской академии наук» Александра Ивановича Татаркина. Данный материал публикуется после ухода из жизни А.И. Татаркина, который участвовал в проведении исследования в составе указанного авторского коллектива. Мы скорбим по поводу безвременного ухода А.И. Татаркина и благодарим его за участие и помощь в проведении исследования. Результаты исследования планируется опубликовать в серии статей. Здесь публикуется первая часть подготовленного материала. Особую благодарность выражаем редколлегии «Вестника Пермского университета. Серия “ Экономика ” » и лично проф. Т.В. Миролюбовой за публикацию статьи.

Авторы статьи также выражают благодарность руководству АО «Карачевский завод “Электродеталь”» за предоставленные для анализа данные (табл. 9).