Определение величины механического износа абразивных зерен при шлифовании

Автор: Ардашев Дмитрий Валерьевич

Журнал: Вестник Южно-Уральского государственного университета. Серия: Машиностроение @vestnik-susu-engineering

Статья в выпуске: 4 т.14, 2014 года.

Бесплатный доступ

Среди различных механизмов износа абразивного инструмента при шлифовании преобладающим является механический, проявляющийся в виде удаления элементарных микрообъемов абразивного материала с рабочей поверхности зерен. Природа образования площадки затупления на зерне в результате данного вида износа до сих пор не раскрыта. В статье предлагается кинетический подход к механическому изнашиванию абразивных зерен при шлифовании на основе термофлуктуационной природы разрушения твердых тел. Полагается, что в результате многократного квазипериодического контакта с обрабатываемым материалом в материале абразивного зерна на межатомных связях возникают перенапряжения, которые служат толчком для преодоления атомами энергетического барьера и разрыва единичной связи. В результате, в абразивном материале происходит накопление разорванных межатомных связей, образуются несплошности и развивается процесс разрушения. При этом немаловажную роль играет температура в зоне обработки. Предложенная методика имитационного моделирования контактного взаимодействия абразивного зерна с материалом позволяет определить напряжения, действующие в зерне при шлифовании и величину долговечности абразивного материала. Установлена характерная зависимость напряжения и долговечности от размера площадки затупления, имеющейся на абразивном зерне. Переход от элементарных объемов абразивного материала, испытывающих напряжения, к макрообъемам позволяет определить величину абразивного материала, изношенного в результате механического взаимодействия с обрабатываемым материалом. Методика прогнозирования величины износа абразивного зерна при эксплуатации шлифовальных кругов различных характеристик в широком диапазоне технологических условий позволит создать совершенно иной подход к проектированию операций абразивной обработки - когда инструмент с определенным ресурсом работоспособности является исходным данным и задача технолога состоит в его эффективной эксплуатации.

Еще

Механический износ абразивного зерна, кинетическая теория прочности, термофлуктуационный механизм разрушения

Короткий адрес: https://sciup.org/147151675

IDR: 147151675

Текст научной статьи Определение величины механического износа абразивных зерен при шлифовании

Одним из факторов, в решающей степени определяющим эффективность операции шлифования, является степень и интенсивность износа абразивного инструмента. Известно несколько механизмов изнашивания абразивных зерен при шлифовании: механический, физико-химический, адгезионный и др. [1–6]. При обработке различных сталей и сплавов указанные механизмы проявляются с различной степенью интенсивности, однако при шлифовании любых материалов механический износ присутствует неизменно [7–15].

Известно, что шлифование – процесс, развивающийся во времени, поэтому представляется возможным трактовать механический износ абразивного зерна при шлифовании с позиций кинетической теории прочности твердых тел под нагрузкой [16]. В ее основе лежит термофлуктуационный механизм разрушения и «временная» зависимость прочности: один и тот же образец, разорванный за короткое время, обладает более высокими прочностными свойствами, чем образец, разорванный медленно.

C позиций кинетической теории прочности разрушение любого твердого тела под нагрузкой трактуется следующим образом. В покое атомы твердого тела совершают достаточно малые колебания на дне потенциальной ямы. Внешняя нагрузка, создавая напряжения в теле, снижает энергоактивационный барьер и возбужденный атом может разорвать межатомную связь с другим атомом. Данное явление происходит по всему телу, естественно, в местах наибольшего напряжения: разрывы межатомных связей накапливаются, в теле появляются несплошности, образуется и развивается локальное нарушение целостности и тело разрушается. Имеется формула долговечности τ для тела, находящегося в сложнонапряженном состоянии – под действием циклических нагрузок [16], что соответствует режиму работы абразивного зерна при шлифовании: число цик- лов нагружения, их длительность и период зависят от кинематических и геометрических харак- теристик схемы шлифования:

I ( i Y^G ) ⁰ ( ,2 kT ^J

^T = N ц t 0

yo exp

2kT где Nц – число циклов, воспринимаемое телом; t0 – время длительности одного цикла, с; I0 – функция Бесселя от мнимого аргумента; γ – коэффициент пропорциональности; σ – величина напряжения в нагружаемом теле, МПа; k – постоянная Больцмана; T – абсолютная температура деформируемого тела, К.

Модель (1) необходимо адаптировать к условиям процесса шлифования, для этого рассмотрим ее параметры.

Параметр N _ц – количество циклов нагружения абразивного зерна в единицу времени – число встреч режущей кромки зерна с обрабатываемым материалом в секунду. Данный параметр зависит от частоты вращения шлифовального круга n к и может быть определен по формуле

N = nk ц 60

Параметр t 0 – длительность контакта режущей кромки абразивного зерна с обрабатываемым материалом полностью зависит от технологических параметров операции шлифования – диаметра шлифовального круга, диаметра обрабатываемой заготовки, скорости круга, скорости заготовки и др. Величина данного параметра целиком и полностью зависит от условий работы абразивного зерна. Применяя известные формулы Е.Н. Маслова [17], можно рассчитать время t ₀ прохождения элементарным сектором шлифовального круга длины дуги контакта на детали L к в условиях круглого наружного шлифования с радиальной подачей:

(

L ¹ +

to = — = —

0 _V _к

60K J у

V к

D • d —д- vSрад

D + d

где V к – скорость шлифовального круга, м/с; D и d – диаметр круга и детали соответственно, мм; n д – количество оборотов детали, мин^–1; v S рад – величина радиальной подачи шлифовального круга, мм/мин.

Параметр γ – элементарный объем абразивного материала, в котором происходят разрывы межатомных связей, их накопление и совершение акта разрушения, см3. В общем случае γ есть элементарный объем материала, в котором происходят все разрушающие твердое тело процессы, иначе его можно назвать коэффициентом пропорциональности между средним напряжением, создаваемым силой, приложенной непосредственно к твердому телу, и напряжением, возникающим в единичной межатомной связи [16]. Величина параметра γ в идеальных телах приблизительно равна 10–23 см3. Для реальных материалов параметр γ имеет различную величину, зависящую как от строения материала, так и от способа его предварительной обработки и состояния. В связи с этим был введен коэффициент перенапряжения межатомных связей q, численно оценивающий различие параметра γ для идеальных твердых тел. Предложенные в [16] выкладки по- зволяют определить величину γ:

_ q • M _ q • M

Y~ Na •p “б•р^Ю23 , где Na – число Авогадро; ρ – плотность материала; М – молекулярная масса.

Параметр Т – абсолютная температура нагружаемого тела, К. В соответствии с имеющимися в научно-технической литературе данными температура отдельных абразивных зерен колеблется в пределах 400–1200 °С, при этом подчеркивается, что зерно нагревается до температуры около 1400 °С и сохраняет тепло в течение сравнительно длительного времени. Для настоящего исследо- вания температура нагружаемого тела – абразивного зерна – принималась в пределах 200–1000 °С, с шагом 200 °С.

Параметр σ – напряжение в теле абразивного зерна, возникающее вследствие действия силы шлифования, направленной вдоль вектора скорости. Одним из возможных решений этой задачи является создание твердотельной модели, проведение численного имитационного моделирования.

С учетом (2)–(4) для условий круглого наружного врезного шлифования формула долговечности абразивного зерна при циклической нагрузке принимает вид:

( q • M

D⋅d д vSрад

D + d

6 ⋅ρ⋅ 10 i,

2 kT

⋅

V к

exp

^ °

q ⋅ M

⋅σ

6 ⋅ ρ ⋅ 10 ²³

2 kT

Определение напряженно-деформированного состояния зерна является трудной задачей, так как в процессе резания зерно находится в сложном напряженном состоянии. Точный расчет такого состояния возможен только с использованием численных методов, в частности метода конечных элементов (МКЭ). При этом возможны два варианта. Первый заключается в создании конечноэлементной модели абразивного зерна с последующим приложением нагрузок, эквивалентных силе резания, действующей на зерно [18, 19]. Недостаток такого подхода заключается в том, что при этом невозможно учесть контактные явления (трение, износ, нагрев зерна и т. д.). Второй подход заключается в том, чтобы численно смоделировать сам процесс резания с учетом некоторых контактных явлений, возникающих при этом. При этом нет необходимости собирать экспериментальные данные о силе резания, действующей на зерно, так как решается контактная задача с отделением стружки. В данной работе был использован второй подход. Для определения величины напряжений в абразивном материале, соответствующей различным условиям шлифования, создана конечно-элементная модель, учитывающая характеристики абразивного и обрабатываемого материала, геометрические и температурные параметры зоны контакта, а также величину площадки затупления, имеющуюся на абразивном зерне. Проведена серия численных экспериментов в пакете твердотельного моделирования ANSYS, результаты которого приведены в табл. 1 и на рис. 1–4.

Таблица 1

Величина напряжения в абразивном зерне

Температура, °С	Зернистость	Площадка затупления l _зат, мм
		0,005	0,10	0,15	0,20	0,25	0,30	0,35	0,40
		Эквивалентные напряжения σ, МПа
200	F90	2097	913	1131	_–	_–	_–	_–	_–
	F60	1944	887	677	809	1053	_–	_–	_–
	F54	870	653	369	416	460	500	_–	_–
	F46	500	470	309	241	291	348	398	573
400	F90	1191	616	943	_–	_–	_–	_–	_–
	F60	871	532	507	669	752	_–	_–	_–
	F54	828	489	361	327	332	408	_–	_–
	F46	488	387	268	211	246	236	308	374
600	F90	1172	203	252	_–	_–	_–	_–	_–
	F60	631	154	175	92	93	107	_–	_–
	F54	509	395	203	168	172	201	142	_–
	F46	417	231	150	119	104	138	147	155
800	F90	404	89,3	76	_–	_–	_–	_–	_–
	F60	388	67	47	42	38	49	_–	_–
	F54	290	201	45	32	28	46	57	_–
	F46	246	177	88	27	23	46	59	67
1000	F90	177	49,7	72	_–	_–	_–	_–	_–
1000	F60	155	39	30	30	30	28	_–	_–

F54	110	52	36	24	20	39	35	_–
F46	109	41	24	19	29	34	55	63

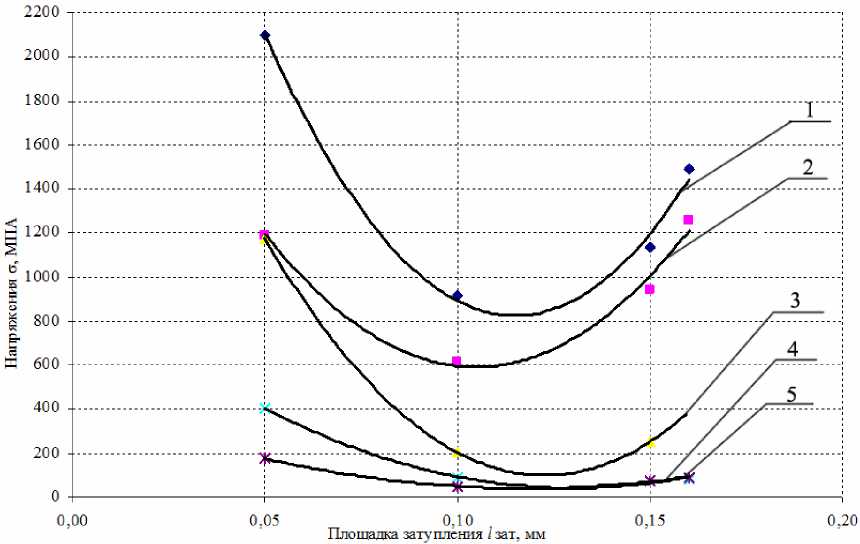
Рис. 1. Зависимость напряжений в абразивном зерне F90 от величины площадки затупления при температурах: 1 – 200 °С; 2 – 400 °С; 3 – 600 °С; 4 – 800 °С; 5 – 1000 °С

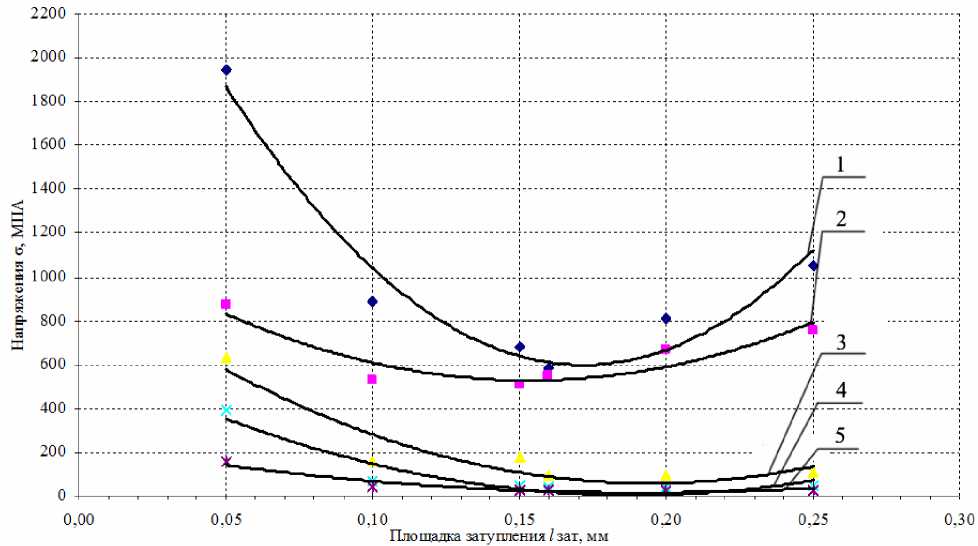
Рис. 2. Зависимость напряжений в абразивном зерне F60 от величины площадки затупления при температурах: 1 – 200 °С; 2 – 400 °С; 3 – 600 °С; 4 – 800 °С; 5 – 1000 °С

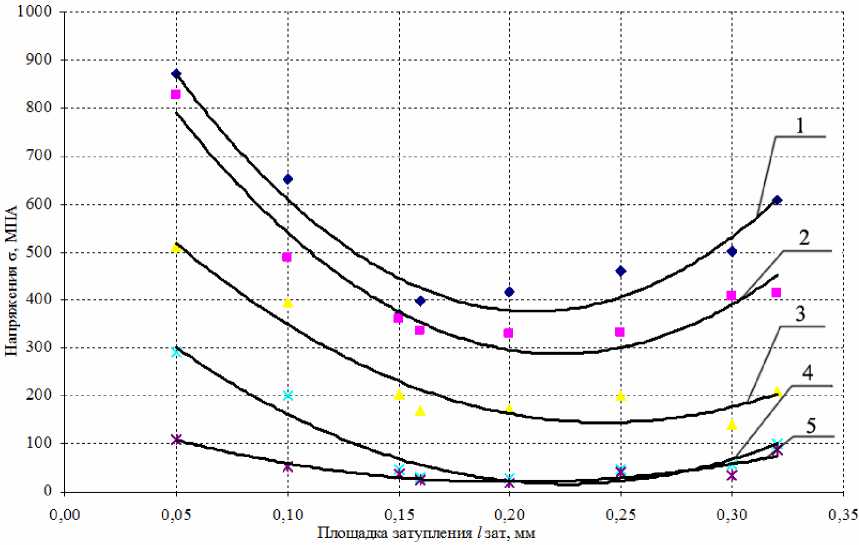
Рис. 3. Зависимость напряжений в абразивном зерне F54 от величины площадки затупления при температурах: 1 – 200 °С; 2 – 400 °С; 3 – 600 °С; 4 – 800 °С; 5 – 1000 °С

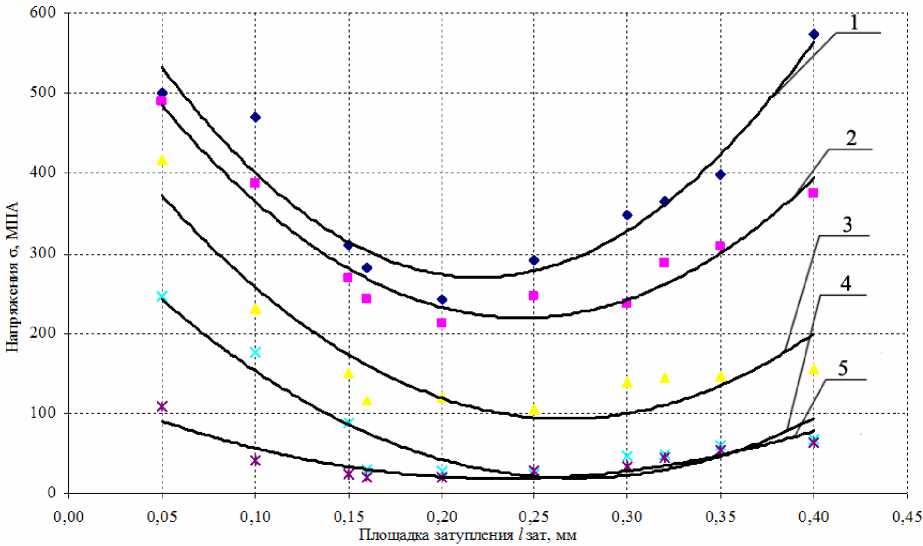
Рис. 4. Зависимость напряжений в абразивном зерне F46 от величины площадки затупления при температурах: 1 – 200 °С; 2 – 400 °С; 3 – 600 °С; 4 – 800 °С; 5 – 1000 °С

Анализируя рис. 1–4, можно заключить, что в начальный период работы зерна на нем образуется и начинает постоянно увеличиваться площадка затупления. Это приводит к снижению напряжений в абразивном материале, что соответствует периоду приработки и образованию на абразивном зерне «наилучшей», с точки зрения работоспособности абразивного зерна, величины площадки затупления, при которой напряжения в теле абразивного зерна минимальны. Дальнейший рост площадки затупления приводит к увеличению напряжения в абразивном зерне, тем более, когда величина площадки затупления сопоставима с размерами самого зерна. Это объясняется уменьшением количества связей в элементарном объеме зерна, воспринимаемых напряжений, а впоследствии существенным увеличением напряжения, действующего на одну связь.

Влияние зернистости абразивного зерна (его геометрических размеров) на величину напряжения в зерне также однозначно: с увеличением номера зернистости при одинаковых температурах и величинах площадки затупления зерна меньшего размера испытывают большие напряжения. Это объясняется опять же наличием в крупных зернах большего количества межатомных связей, воспринимающих внешнюю нагрузку.

Долговечность абразивного зерна, рассчитанная по формуле (5) для различных условий его работы, приведена в табл. 2 и на рис. 5–8.

На рис. 5–8 можно выделить три основных участка – начальный период, когда с обрабатываемой заготовкой контактирует острое зерно и на нем начинает образовываться площадка затупления, период стабильной работы, на котором площадка достигает своего оптимального значения, при котором долговечность абразивного зерна максимальна и период интенсивного износа зерна, при котором площадка увеличивается до размеров, сопоставимых с размерами самого зерна и происходит существенное уменьшение его долговечности.

Увеличение температуры в зоне контакта абразивного зерна с обрабатываем материалом приводит к увеличению величины долговечности абразивного зерна: это связано со снижением прочностных свойств обрабатываемого материала [20]. Абразивные зерна больших размеров (зернистостей) обладают большей долговечностью, нежели зерна меньших размеров, работающие в тех же технологических условиях. Так, увеличение размеров зерна в 1,5 и 2,5 раза увеличивает долговечность в 2,4 и 4 раза соответственно.

Таблица 2

Долговечность абразивного зерна в различных условиях

Температура, ° С	Зернистость	Площадка затупления l _зат, мм
		0,05	0,10	0,15	0,20	0,25	0,30	0,35	0,40
		Долговечность τ, c
200	F90	0,23	0,55	0,40	_–	_–	_–	_–	_–
	F60	0,24	0,62	0,69	0,45	0,36	_–	_–	_–
	F54	0,36	0,65	0,93	1,03	0,78	0,48	_–	_–
	F46	0,48	0,49	0,61	0,69	0,63	0,58	0,54	0,45
400	F90	0,37	0,67	0,55	_–	_–	_–	_–	_–
	F60	0,43	0,91	0,99	0,63	0,42	_–	_–	_–
	F54	0,44	0,93	1,24	1,65	1,30	0,92	_–	_–
	F46	0,58	0,65	0,79	0,90	0,83	0,84	0,73	0,66
600	F90	0,42	0,86	0,45	_–	_–	_–	_–	_–
	F60	0,58	1,00	1,17	0,84	0,46	_–	_–	_–
	F54	0,65	1,26	1,67	2,16	2,07	1,61	_–	_–
	F46	0,72	0,98	1,25	1,43	1,55	1,52	1,43	1,22
800	F90	0,81	1,62	1,18	_–	_–	_–	_–	_–
	F60	0,83	1,27	1,54	1,36	1,10	_–	_–	_–
	F54	0,97	1,50	1,92	2,25	2,03	1,64	_–	_–
	F46	1,06	1,60	2,46	3,20	3,37	3,06	2,42	1,70
1000	F90	1,42	2,57	0,78	_–	_–	_–	_–	_–
1000	F60	1,54	2,21	2,46	1,93	1,27	_–	_–	_–

F54	1,56	2,00	2,49	2,61	1,99	1,66	_–	_–
F46	1,90	3,11	3,66	3,86	3,66	3,31	2,74	2,09

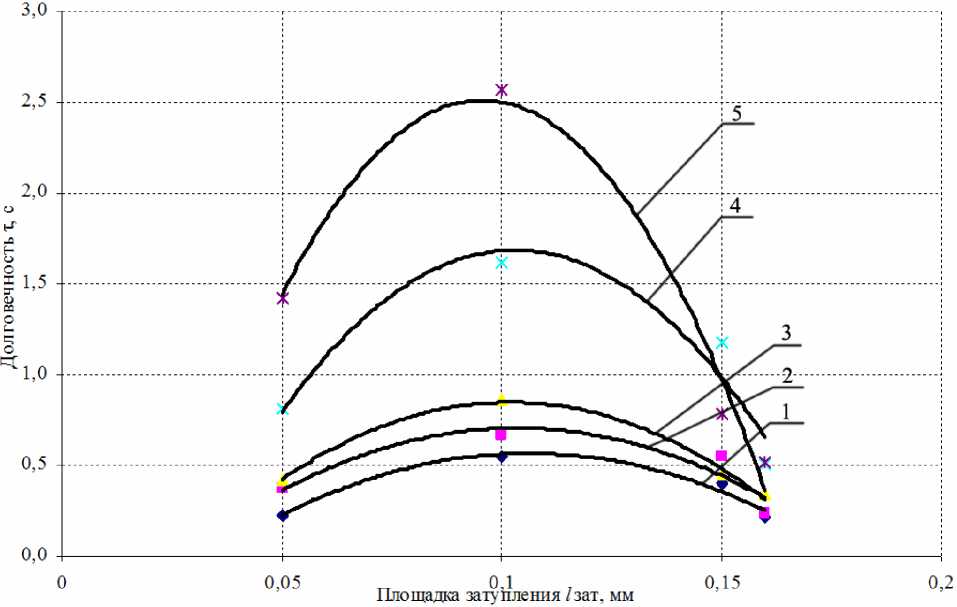
Рис. 5. Зависимость долговечности абразивного зерна F90 от величины площадки затупления при температурах: 1 – 200 °С; 2 – 400 °С; 3 – 600 °С; 4 – 800 °С; 5 – 1000 °С

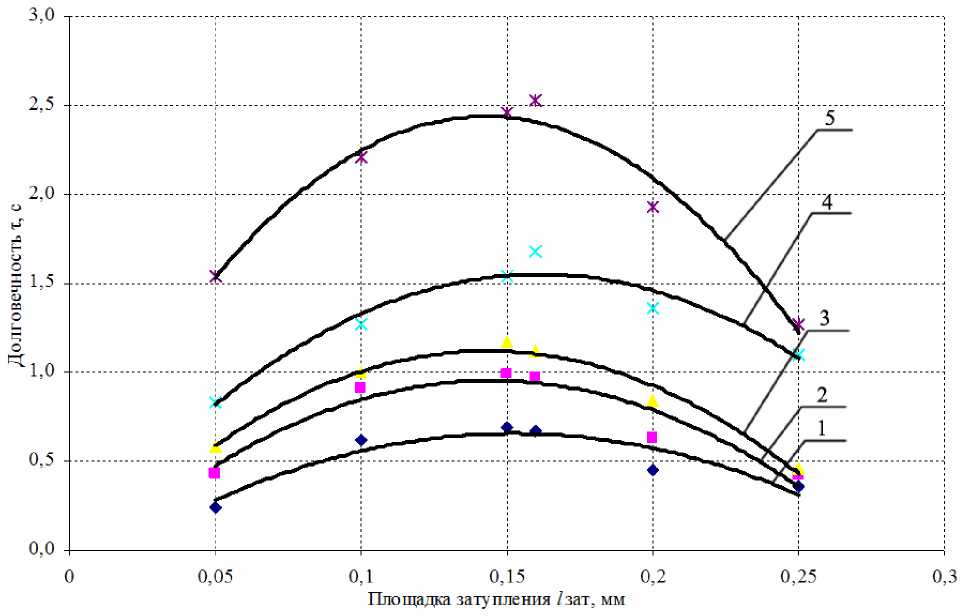
Рис. 6. Зависимость долговечности абразивного зерна F60 от величины площадки затупления при температурах: 1 – 200 °С; 2 – 400 °С; 3 – 600 °С; 4 – 800 °С; 5 – 1000 °С

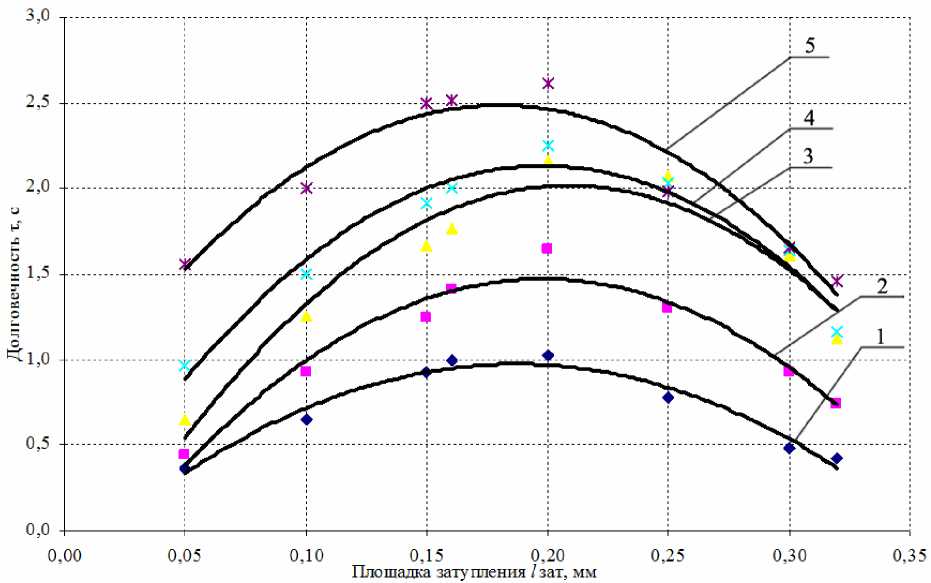
Рис. 7. Зависимость долговечности абразивного зерна F54 от величины площадки затупления при температурах: 1 – 200 °С; 2 – 400 °С; 3 – 600 °С; 4 – 800 °С; 5 – 1000 °С

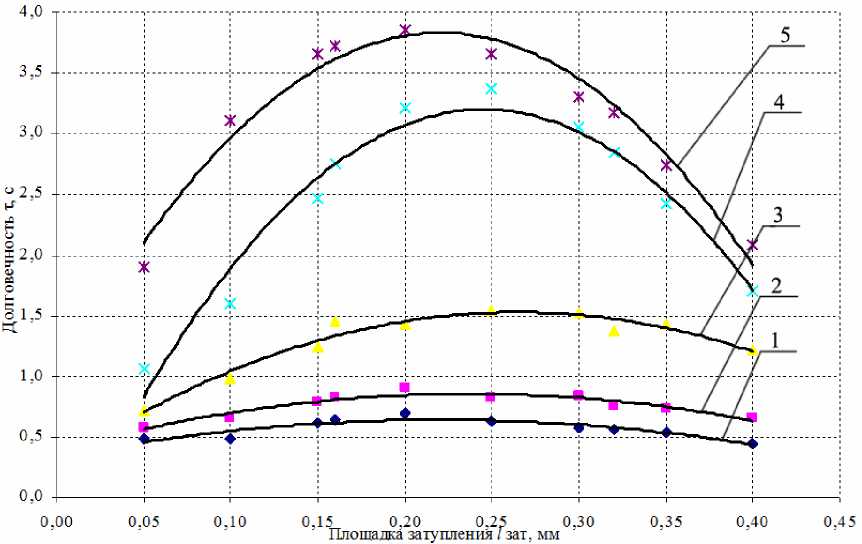
Рис. 8. Зависимость долговечности абразивного зерна F46 от величины площадки затупления при температурах: 1 – 200 °С; 2 – 400 °С; 3 – 600 °С; 4 – 800 °С; 5 – 1000 °С

Определение величины объема элементарной части абразивного зерна, испытывающего напряжения σ и удаляемой по истечении периода долговечности τ, может быть произведено средствами пакета Ansys, в котором выполнялось имитационное моделирование взаимодействия абразивного зерна с обрабатываемым материалом. Для этого посредством команд, связанных с параметризацией модели, сначала визуализируется номер элемента, испытывающий максимальные напряжения, затем командой Get scalar data, с предварительным указанием в качестве одного из параметров Elements volume, а также номера требуемого элемента, формируется файл, в котором записаны требуемые параметры модели, в том числе и величина объема требуемого элемента в мм3.

Найденные по описанной выше методике величины элементарных объемов w _а ^м _. _з ^ех материала, испытывающих напряжения в абразивном зерне, приведены в табл. 3.

Следует отметить, что параметры твердотельной модели абразивного зерна одинаковы для всех технологических условий работы – обрабатываемые материалы, температуры в зоне контакта, материал зерна. Значит, приведенные в таблице данные можно использовать для различных сочетаний «абразивное зерно-обрабатываемый материал».

Таблица 3

Элементарные объемы абразивного материала, испытывающие напряжения при контакте с обрабатываемым материалом

Зернистость	Площадка затупления l _зат, мм
	0,005	0,10	0,15	0,16	0,20	0,25	0,30	0,32	0,35	0,40
	Величина элементарного объема w _а ^м _.з ^ех , 10^–5, мм³
F90	0,100	0,289	0,321	0,597	_–	_–	_–	_–	_–	_–
F60	0,091	0,240	0,267	0,495	0,891	0,955	_–	_–	_–	_–
F54	0,062	0,139	0,235	0,386	0,695	0,745	0,817	0,974	_–	_–
F46	0,040	0,090	0,153	0,251	0,452	0,484	0,613	0,633	0,701	0,825

В итоге, учитывая плотность абразивного материала ρ, данные табл. 2 и 3, а также время работы круга Тк, можно рассчитать суммарный весовой износ абразивного зерна по формуле мех

W _а ^м _з ^ех = ρ ^w ^а ^. ^з ^T ^к . (6)

. _τ

Результаты расчетов для условий работы острого абразивного зерна ( l з = 0,005 мм) по истечении 30 с шлифования приведены в табл. 4.

Таблица 4

Масса изношенной части абразивного зерна

	Температура в зоне контакта, °С
Зернистость	200	400	600	800	1000
Зернистость	Масса изношенной части абразивного зерна, W _а ^м _.з ^ех , 10^–7, г
F90	5,54	4,19	3,03	1,58	0,91
F60	4,42	2,47	1,84	1,28	0,69
F54	2,01	1,64	1,12	0,75	0,47
F46	0,99	0,81	0,66	0,44	0,25

Приведенные в табл. 4 данные показывают влияние размеров абразивного зерна и температуры в зоне контакта с обрабатываемым материалом на величину износа зерна в результате его механического взаимодействия с обрабатываемым материалом. При увеличении номера зернистости величина механического износа абразивного зерна уменьшается, при этом с увеличением контактной температуры эта разница становится меньше. При температурах от 1000 °С и выше начинают превалировать процессы износа, имеющие иную природу, возможно, на первый план выходит физико-химическое изнашивание абразивного материала [21].

Данные, полученные в результате имитационного моделирования процессов контактного взаимодействия абразивного зерна с обрабатываемым материалом, а также расчетов износа абразивного зерна, в основу которых положена термофлуктуационная трактовка прочности абразивного материала, позволят в дальнейшем создать комплексную имитационную модель износа абразивного зерна, которая позволит прогнозировать величину изношенной части абразивного инструмента в любой момент времени его работы. Решение данной задачи позволит разработать инновационную методику режимно-инструментального оснащения групповой технологии шлифования на основе прогнозирования работоспособности абразивных инструментов [22].

Выводы:

1. Предложена методика определения величины износа абразивного зерна в результате механического взаимодействия с обрабатываемым материалом на основе имитационного моделирования кинетической прочности абразивного зерна при шлифовании.
2. Установлено однозначное влияние на величину этого износа температуры в зоне шлифования, степени затупления абразивного зерна, а также его размеров.
3. Присутствие в предложенной методике параметров обрабатываемого материала, характеристики инструмента, степени затупления абразивных зерен, времени работы инструмента создает предпосылки создания методики проектирования эффективных абразивных операций на основе прогнозирования работоспособности абразивных инструментов, с учетов различных механизмов их изнашивания.

Список литературы Определение величины механического износа абразивных зерен при шлифовании

Носенко, В.А. Технология шлифования металлов: моногр./В.А. Носенко, С.В. Носенко. -Старый Оскол: ТНТ, 2013. -616 с.
Носенко, В.А. Влияние контактных процессов на износ круга при шлифовании/В.А. Носенко//Инструмент и технологии. -2004. -№ 17-18. -С. 162-167.
Носова, И.В. Влияние физико-химических реакций в контакте абразивное зерно-металл на показатели шлифования/И.В. Носова, В.М. Шумячер//Технология машиностроения. -2013. -№ 4. -С. 14-17.
Лоладзе, Т.Н. Прочность и износостойкость режущего инструмента/Т.Н. Лоладзе. -М.: Машиностроение, 1982. -320 с.
Мишнаевский, Л.Л. Износ шлифовальных кругов/Л.Л. Мишнаевский. -Киев: Наукова думка, 1982. -188 с.
Hitchiner, M.P. Some remarks on the chemical Wear of diamond and cubic BN during turning and grinding/M.P. Hitchiner J. Wilks//Wear. -1987. -Vol. 114. -P. 327-338.
Reducing tool wear in abrasive cutting/R. Neugebauer, K.-U. Hess, S. Gleich, S. Pop//International Journal of Machine Tools & Manufacture. -2005. -Vol. 45. -P. 1120-1123
Conditioning and monitoring of grinding wheels/K. Wegener, H.-W. Hoffmeister, B. Karpuschewski et al.//CIRP Annals. Manufacturing Technology. -2011. -Vol. 60. -P. 757-777.
2D/3D ground surface topography modeling considering dressing and wear effects in grinding process/J.L. Jiang, P.Q. Ge, W.B. Bi et al.//International Journal of Machine Tools and Manufacture. -2013. -Vol. 74. -P. 29-40.
Kumar, S Prediction of wear and surface roughness in electro-discharge diamond grinding/S. Kumar, S.K. Choudhury//Journal of Materials Processing Technology. -2007. -Vol. 191. -P. 206-209.
LaChance, S. Development of an Automated System for Measuring Grinding Wheel Wear Flats/S. LaChance, A. Warkentin, R. Bauer//Journal of Manufacturing Systems. -2003. -Vol. 22. -P. 130-135.
Brinksmeier, E. Monitoring of Grinding Wheel Wear/E. Brinksmeier, F. Werner//CIRP Annals -Manufacturing Technology. -1992. -Vol. 41. -P. 373-376.
Tönshoff, H.K. Process Monitoring in Grinding/H.K. Tönshoff, T. Friemuth, J.C. Becker//CIRP Annals. Manufacturing Technology. -2002. -Vol. 51. -P. 551-571.
A study on Wear mechanism and Wear reduction strategies in grinding wheels used for ELID grinding/K. Fathima, A. Senthil Kumar, M. Rahman, H.S. Lim//Wear. -2003. -Vol. 254. -P. 1247-1255.
Xipeng, X. Mechanisms of abrasive Wear in the grinding of titanium (TC4) and nickel (K417) alloys/X. Xipeng, Y. Yiqing, H. Huang//Wear. -2003. -Vol. 255. -P. 1421-1426.
Регель, В.Р. Кинетическая теория прочности твердых тел/В.Р. Регель, А.И. Слуцкер, Э.Е. Томашевский. -М.: Наука, 1974. -560 с.
Маслов, Е.Н. Теория шлифования материалов/Е.Н. Маслов. -М.: Машиностроение, 1974. -320 с.
Шмидт, И.В. Напряженное состояние полимерно-композитной слоистой системы при механической обработке резанием/И.В. Шмидт//Наукоёмкие технологии в машиностроении. -2013. -№ 7. -С. 27-31.
Shmidt, I.V. Modeling of Stressed State during the Processing of Laminated Surfaces/I.V. Shmidt, A.A. Dykonov//Proceedings of The World Congress on Engineering and Computer Science 2014. International Association of Engineers (IAENG). -Р. 914-917.
Дьяконов, А.А. Научно-методическая база повышения эффективности процессов абразивной обработки на основе многофакторной оценки обрабатываемости материалов/А.А. Дьяконов//Наукоёмкие технологии в машиностроении. -2013. -№ 1. -С. 19-26.
Ардашев, Д.В. Физико-химический износ в процессах шлифования/Д.В. Ардашев//Трение и износ. -2014. -№ 4. -С. 437-443.
Ардашев, Д.В. Режимно-инструментальное оснащение проектирования групповой технологии операций шлифования/Д.В. Ардашев//Фундаментальные и прикладные проблемы техники и технологии. -2011. -№ 4/2(288) -С. 14-19.

Еще

Статья научная