Определение вероятности отказов агрегатов наддува двигателя КАМАЗ - 740.63.400

На сегодня основная доля агропромышленного автопарка состоит преимущественно из дизельных двигателей, оснащенных агрегатами наддува. Таким образом, в качестве объекта исследования выступает широко распространенный в агропромышленном секторе дизельный двигатель КАМАЗ-740.63.400, оснащаемый турбокомпрессорами марки ТКР-7 и их аналогами. Условия работы данных агрегатов наддува обусловлены высокой угловой скоростью вращения ротора турбокомпрессора, резкой сменой режимов работы турбокомпрессора из-за нестационарного режима работы двигателя, а также высокой теплонагруженностью деталей турбокомпрессора. Интенсивная эксплуатация данных комбинированных двигателей в дан- ных условиях значительно снижает надежность данного узла, что приводит к его преждевременной замене. Так, ресурс турбокомпрессора должен быть не менее ресурса двигателя, на котором он применяется [3]. Для двигателя КАМАЗ-740.64.400 он составляет 800 тыс. км пробега [5].

Актуальность данного научного исследования обусловлена задачей увеличения срока эксплуатации агрегатов наддува дизельных двигателей сельскохозяйственного назначения, при этом большое внимание уделяется диагностике неисправностей данных агрегатов.

Полученные результаты позволят определить вероятность отказа турбокомпрессора в зависимости от пробега, что позволит оптимально организовать необходимые мероприятия по диагностированию основных неисправностей агрегатов наддува.

Постановка задачи

В качестве объекта исследования выступают дизельные двигатели КамАЗ-740.63.400 в количестве n = 15 шт., для которых выявлены следующие наработки на отказ связанных с агрегатами наддува: 58500, 63000, 65300, 67200, 68000, 70300, 75500, 76500, 78800, 82300, 84700, 85600, 87300, 91300, 93700 км пробега [1]. Проанализируем данную выборку с помощью нормального закона распределения [2, 4].

Построим интервальный ряд распределения.

Число групп приближенно определяется по формуле Стэрджесса (1):

n = 1 + 3, 2lg ( n ).

Ширина интервала рассчитывается по формуле (2):

, X - X . max      min

.

n

Границы группы распределения представлены в таблице 1.

Таблица 1

Значения границ групп распределения

Номер группы	Нижняя граница	Верхняя граница
1	58500	65540
2	65540	72580
3	72580	79620
4	79620	86660
5	86660	93700

Конечные данные для расчета оформим в таблицу 2.

Таблица 2

Данные для расчета показателей

Группы	Середина интервала, x центр	Частота, fi	xifi	Накопленная частота, S	i x - x cp i • f	( x - x cp )2 • f ;	Относительная частота, fi / f
58500 - 65540	62020	3	186060	3	42240	594739200	0,2
65540 - 72580	69060	3	207180	6	21120	148684800	0,2
72580 - 79620	76100	3	228300	9	0	0	0,2
79620 -86660	83140	3	249420	12	21120	148684800	0,2
86660 -93700	90180	3	270540	15	42240	594739200	0,2
Итого		15	1141500		126720	1486848000	1

Оценка ряда распределения осуществляется по нижеследующим показателям. Средняя взвешенная (выборочная средняя)

• - Z xf

x =    ---.

Z f

В нашем случае выборочная средняя равняется показателю 76100.

Мода

M = x _n + h -------²---¹------,

°   ⁰    ( f 2 — f l ) + ( f 2 — f0

где x – начало модального интервала; h – величина интервала; f 2 – частота, соответствующая модальному интервалу; f 1 – предмодальная частота; f 3 – послемодальная частота.

Начальное значение интервала равно 58500 км пробега. По результатам расчета по формуле 4, наиболее часто встречающееся значение ряда – 65540 км.

Медиана

В качестве медианного интервала принимаем значения от 58500 - 65540, так как накопленная частота S данного интервала больше значения медианного номера.

Me = x ₀ + — ^ ^ f ⁰ f me

—

v

° me - 1

.

В результате расчета определили, что 50% значений выборки меньше показателя 76100 км.

Среднее значение изучаемого признака по способу моментов

• -    x \ f ,    ,

  
  

x = V^-h + A,

Z. f где А – условный нуль, равный варианту с максимальной частотой (середина интервала с максимальной частотой); h – шаг интервала.

x' =

xi — A

.

h

Согласно расчетам, принимаем показания А = 62020 км; шаг интервала h = 7040 км; 76100 км.

x =

Средний квадрат отклонений по способу моментов рассчитывается по формуле 7.

D = ^[  /^J Jt . h ² + ₍ x - a ) ² .

Z fi

Таблица 3

Исходные данные для расчета среднеквадратичного отклонения

x центр	x \.	x \f	[ x 'J2 f i
62020	0	0	0
69060	1	3	3
76100	2	6	12
83140	3	9	27
90180	4	12	48
Итого:	10	30	90

Среднее квадратическое отклонение находим из выражения 8.

a = D5 .                                 (8)

Усредненный показатель, на который отличается от среднего выборочного значения каждое значение ряда, составляет 9956 км.

Показатели вариации

Размах вариации – показатель, позволяющий оценить пределы, в которых изменяется величина признака изучаемой выборки.

^R = x max - x min ^.

Среднее линейное отклонение (9) вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности.

E | x ^{- x} i L E f

Среднее значение, на которое отличается каждое значение ряда от другого, составляет 8448 км.

Коэффициент вариации рассчитываем по формуле 10.

v = - 100% .                                (10)

x

Поскольку v =13%≤ 30%, то совокупность однородна, а вариация слаба. Полученным результатам можно доверять.

Проверка гипотез о виде распределения

Проверку гипотезы о нормальном распределении выполним с помощью критерия согласия Пирсона (11).

K = E fM ,                (11)

f • Pi где p, - вероятность попадания в i-й интервал случайной величины, распределенной по гипо тетическому закону.

Вычисление вероятностей p осуществляется по формуле и таблице функций Лапласа.

Ф

к 5    7

—

к 5  7

где s = 9956 км; x = 76100 км оценены по выборке.

Теоретическая (ожидаемая) частота равна f = f • Ри где f = 15.

Вероятность попадания в i -й интервал:

Pi =^{Ф ( Х} 2 ) ^{-Ф ( Х} 1 ) .

Определим границу критической области. Критическая область для статистики Пирсона всегда правосторонняя: [ К^ ; +^ ) .

Границу К^ = % ² ( k - r - 1; а ) определяем по таблицам распределения % ² и заданным значениям а , k, r = 2 .

В результате расчета наблюдаемое значение статистики Пирсона меньше значения критической области К^ = % ² ( 5 - 2 - 1;0,05 ) = 5,99146 >  К_набл = 2,67 , поэтому можно сделать вывод о том, что выборка имеет нормальное распределение.

Результаты расчета вероятности отказов

Таблица 4

x i ^ x i + 1	f i	X = ( Xi - x cp )/ 5	x 2 = ( x i + 1 - x cp )! 5	ф ( x i )	Ф ( x 2 )	Pi =Ф ( x 2 ) — Ф ( X i )	Ожидаемая частота, 15 P i	Слагаемые статистики Пирсона, Ki
58500 -65540	3	-1,7078	-1,0247	-0,4564	-0,3485	0,1079	1,6185	1,1792
65540 - 72580	3	-1,0247	-0,3416	-0,3485	-0,1368	0,2117	3,1755	0,0096
72580 - 79620	3	-0,3416	0,3416	-0,1368	0,1368	0,2736	4,104	0,2969
79620 -86660	3	0,3416	1,0247	0,1368	0,3485	0,2117	3,1755	0,0096
86660 -93700	3	1,0247	1,7078	0,3485	0,4564	0,1079	1,6185	1,1792
							Итого:	2,6745

Выводы

• 1.    Подтверждена гипотеза о нормальном распределении данной выборки с помощью критерия Пирсона.

• 2.    По результатам вероятностной оценки (рис.), наиболее критическая область плотности возникновения отказов, связанных с неисправностями агрегатов наддува, лежит в интервале от 72580 до 79620 км пробега. В интервале от 58500-79620 км пробега вероятность отказов турбокомпрессора составит 60%, что предполагает незапланированные затраты на ремонт и техническое обслуживание, что приводит к простою данного количества агрегатов.

• 3.    Оценка полученных данных позволяет сделать вывод об актуальности разработки и модернизации методик диагностирования неисправностей агрегатов наддува дизельных двигателей автомобилей КамАЗ.

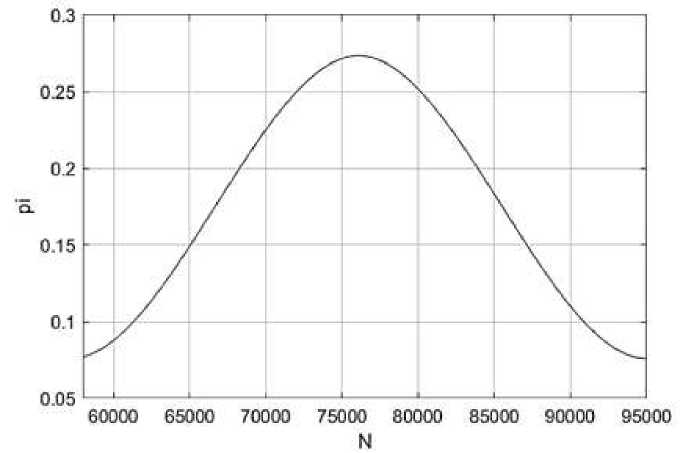
Рисунок – Кривая плотности распределения вероятности отказов агрегатов наддува двигателя КамАЗ-740.63.400