Определение вероятности устойчивости систем импульсного регулирования по методу Г. С. Черноруцкого
Автор: Смирнов Юрий Сергеевич
Статья в выпуске: 1 т.14, 2014 года.
Бесплатный доступ
Предложено развитие метода Г.С. Черноруцкого для определения вероятности устойчивости стохастических нелинейных систем импульсного регулирования (СИР). Рассмотрены два случая определения выполнения условий устойчивости мехатронных систем (МС), когда число параметров, имеющих «большие» вариации, не превышает двух. Произведена квадратичная суммарная оценка качества системы в плоскости ее случайных параметров. Приведены области устойчивости для ряда простейших СИР.
Стохастические, нелинейные мехатронные системы импульсного регулирования, определение вероятности устойчивости, квадратичная суммарная оценка
Короткий адрес: https://sciup.org/147154953
IDR: 147154953 | УДК: 681.5
Текст научной статьи Определение вероятности устойчивости систем импульсного регулирования по методу Г. С. Черноруцкого
В первом примере случайными являются коэффициент K ˆ передачи прямого контура и одна из постоянных времени Т ˆ типовых звеньев.
В соответствии с методикой, развитой в работе Г.С. Черноруцкого [1], вероятность устойчивости системы регулирования может быть определена по выражению
P { q i ,q 2 e0 y } = JJ f ( q i , q 2 ) dqxdq 2 , (1)
®y где q1, q2 - случайные параметры системы регулирования; f (q1, q2) - совместная плотность ве роятности случайных величин; 0y - область устойчивости.
Рассмотрим простейшую СИР, структурная схема которой приведена на рис. 1, а непрерыв- ная часть системы имеет передаточную функцию [2]:
А
K
Р ( Tp + 1 )
W (Р ) =
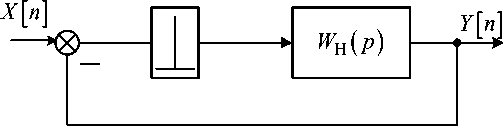
Рис. 1
Импульсная передаточная функция разомкнутой СИР определяется дискретным преобразованием Лапласа весовой функции непрерывной части [3]:
да
W (q ) = D {k [ n ]} = £ k [ n ]• e- qn, (3)
n = 0
или Z -преобразованием [4]:
да
W ( z ) = Z { k [ n ] } = £ k [ n ] . Z - n , (4)
n = 0
где k [ n ] - решетчатая функция, соответствующая весовой функции приведенной непрерывной части СИР. В дальнейшем будет пользоваться метод Z -преобразования. В соответствии с выражением (4) импульсная передаточная функция будет иметь вид
W ( z ) = K —
—
к
z — 1
z
—
z
e
.— Ty /T
где Т у – период импульсов управления.
Замкнутая СИР будет устойчива [3], если корни характеристического уравнения замкнутой системы по модулю меньше единицы:
| Z\ < 1. (6)
Для использования критериев устойчивости, разработанных для непрерывных систем, очевидно, необходимо отобразить внутренность единичного круга в плоскости Z на левую полуплоскость комплексной области, что может быть выполнено билинейным преобразованием вида [3]:
Z = 1^ . (7)
1 — to
Тогда для определения области устойчивости импульсной системы можно воспользоваться критерием Гурвица. Характеристическое уравнение замкнутой СИР для рассматриваемого случая будет иметь вид
1 + W (z ) = a 2 z2 + a1 z + a 0 = 0,(8)
где d = e~—y —, а коэффициенты принимают значения a 2 = 1; а1 =(1 + d) + K (1 — d); a о = d.(9)
Область устойчивости задается системой трех неравенств вида [4]:
a 2 + a 1 + a 0 > 0;
a2 — a1 + a0 > 0;(10)
a 2 — a 1 > 0.
Осуществив элементарные преобразования, будем иметь следующие неравенства: K > 0;
1 — e
— T y / T
> 0;
K < 2
1 + e
— T y / T
1 — e
— T y / t ,
дающие область устойчивости рассматриваемой импульсной системы. Определяем асимптоту границы устойчивости в виде
T , K =t — + b , T y
где lim 2
— y — >'
1 + e — «T
— y, — - ( 1 — e"— y' — )
b = lim
— y —T
1 + e
— T y —
1 — e
— T y —
— T T y —
Раскрыв неопределенность по правилу Лопиталя, будем иметь уравнение асимптоты: T
K = 4 F . (13)
T y
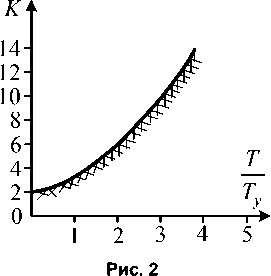
Область устойчивости для этого случая приведена на рис. 2.
Следует отметить, что выражение (12) достаточно быстро стремится к своей асимптоте, так например, если T/T y = 2 , отклонение А составляет ® 2 %, то при T—y = 3 - уже 0,8 %.
На рис. 3 показан график изменения этой ошибки в зависимости от значения T T y .
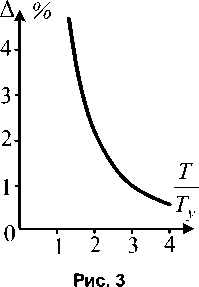
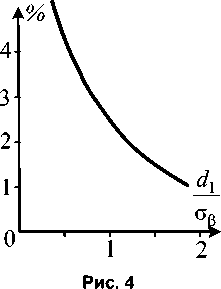
Положим, что параметры K ˆ и T ˆ деленными по нормальному закону:
_ ( K - m K ) 2
являются случайными независимыми величинами, распре-
f(K )=7207 e" "K ; f (T )=
1 - e
2 o T
( T - m T ) 2 2 a T
.
В этом случае вероятность выполнения условия устойчивости может быть вычислена по выражению (1), учитывая, что совместная плотность вероятности двух независимых случайных величин равна произведению плотностей:
P {K, T Ny }=J J /к (К )■ fT (T) -K ■ -T
0 ^y mT — 3aT
В тех случаях, когда — T ----— > 2 с достаточной для инженерной практики точностью, вы-
Ty числение вероятности выполнения условий устойчивости может быть выполнено по выражению
^ ^
P{К,Te0y ■ - + Ф -L
2 <ор J где d1 – расстояние от границы устойчивости, заданной своей асимптотой, до центра рассеивания случайных величин Kˆ и Tˆ :
О р = ^ о T cos2 в + о К sin2 в . (17)
Преобразуем выражение (16) исходя из очевидных геометрических соображений:
P { К, T G0 y } « 2 + Ф
mT
тк • 0,97 4
°Р
2 16 2 1
где oR =. Пт — + о^ —, в V T 17 К 17, mK
4 mT
Т y
mT — 3 a
В случаях, когда — T ----< 2, вычисления необходимо производить или при помощи вычис-
Ty лительной техники, либо с использованием сеток рассеивания.
Приближенно вероятность устойчивости может быть вычислена, исходя из следующих соображений. Определим минимальное расстояние между центром рассеивания случайных величин и границей устойчивости. которое, очевидно, будет равно длине отрезка нормали к границе устойчивости, проходящей через центр рассеивания. Определив угол в и вычислив О р , по выражению (16), определим приближенное значение вероятности устойчивой работы системы. Обычно требуемая вероятность выполнения условий устойчивости близка к единице. Очевидно, что с увеличением - 1 / О р в (16) ошибка определения вероятности устойчивости будет уменьшаться.
На рис. 4 приведена зависимость ошибки в определении вероятности выполнения условий устойчивости по выражению (16) в зависимости от d1 /ор . Отметим то обстоятельство, что вы- mT 37 числение по выражению (16) при —T---— < 2 дает заниженные результаты.
T y
Если случайными параметрами в системе являются постоянная времени T ˆ и период управления T y , то уравнение границы устойчивости может быть записано в виде
^ + 2
T — T - In------; K > 2. (19)
y K - 2
Если T и T ˆ y имеют нормальный закон распределения плотности вероятности и независимы, вероятность выполнения условий устойчивости может быть вычислена по выражению:
где
P { T y . T ^ } — 2 + Ф
d 1 —
mT
- In
K + 2
K - 2
Ф — arctg I In
d 1
° p
m
T y
cos ф ;
K + 2
K - 2
22 22
O p — JO T Sin ф + о T cos ф .
Рассмотрим второй пример, когда случайными являются приведенный к валу электродвигателя момент инерции J ˆ и вязкое демпфирование B ˆ .
В ряде реальных ЭМТП непрерывная часть СИР имеет вид
W ( P ) = . (21)
P (-Jp + ^?)
Каноническая форма записи передаточной функции будет иметь вид KB
(p) P (JP^ +1).
Таким образом, случайными величинами являются коэффициент усиления и постоянная времени. Однако распределение плотности вероятности K B ˆ и J ˆ B ˆ будет отличным от нормального, если J ˆ и B ˆ имеют нормальный закон распределения плотности вероятности.
Уравнение границы устойчивости в плоскости двух случайных параметров J ˆ и B ˆ имеют вид
ˆ T y B ˆ
.
J
, K + 2 B ln
K - 2 B
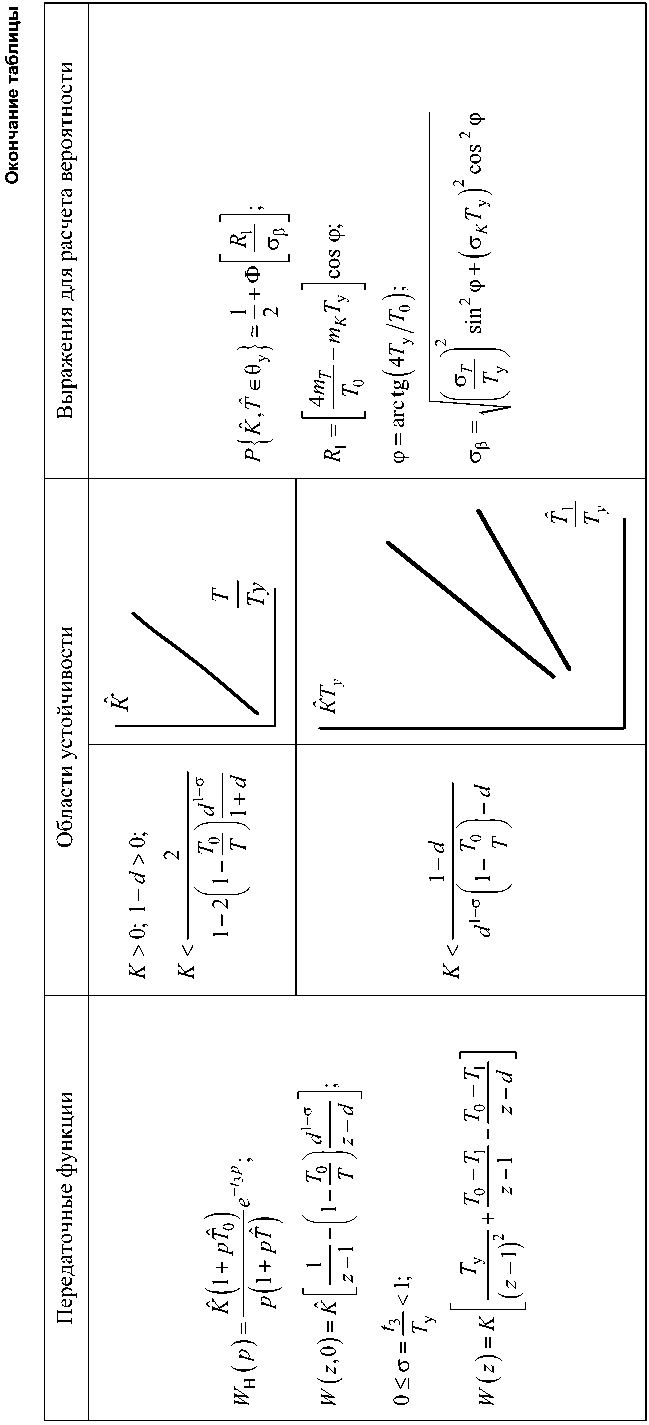
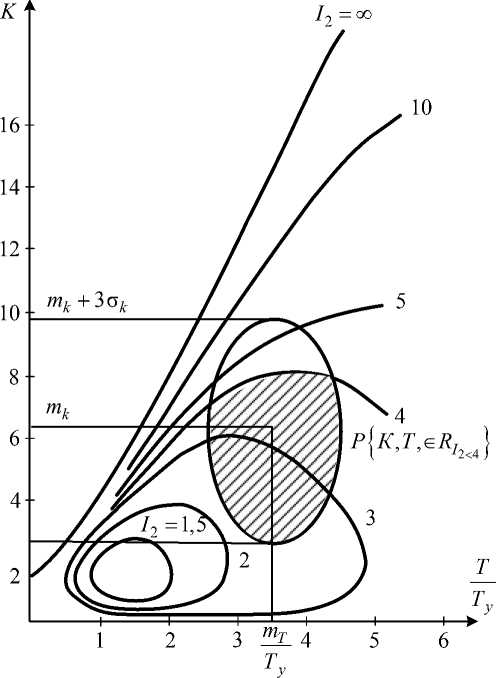
Если выполняется условие mj - 3 J o j mB - 3oB >2Ty, то выражение (23) может быть преобразовано к виду .J « KTy/4. Тогда вероятность устойчивости СИР можно определить по выражению P {J, B G0 y }— 2 + Ф k1-, oJ J где k1 – расстояние от центра рассеивания до границы области устойчивости. Рассмотрим СИР [2], имеющую передаточную функцию непрерывной части: Ke—tзp W (p )=;13< Ty. p (Tp+1) Импульсная передаточная функция разомкнутой системы, полученная при помощи модифи- цированного Z-преобразования [1 , имеет вид W (--.»)=K A z — 1 — e - Ty /T z — d , а коэффициенты характеристического уравнения равны: a0= к (d1—:— d) + d . g=0,05 a2 = 1; a1 = к(1 — di^) — 1 — d; 10 — 8 — 6-- g— 0,2 5 10 Рис. 5 Область устойчивости задается системой нера- 22 — 20 — 18 — 16 — 14- 12-- g=0,1 g= 0,3 g= 0,5 ---------- ct=0,7 , ct=0,8 T1 Т y венств: K > 0; к < —2 , ; 1—2 d1:: 1 — d > 0; к < d1—:— d . 1 + d Область устойчивости в плоскости двух случайных параметров показана рис. 5. Если наложены ограничения на значения параметров вида mT — 3:T > 2 +1/4тк , а параметры являются нормальными независимыми случайными величинами, то вероятность устойчивости приближенно определяется выражением P {к, t G0y }=2+Ф где d 1 = — e 1 — e - Ty И ,—Ty/mT (M — d1 _:к J e-Ty!mT " , Квадратичная суммарная оценка качества СИР Сам по себе факт выполнения условий устойчивости еще не гарантирует получения приемлемых качественных показателей системы регулирования. Как и для непрерывных систем, для оценки качества импульсных систем регулирования широко используются интегральные и суммарные оценки качества, степень устойчивости, степень колебательности [3, 4]. Нужно отметить, что применение квадратичной суммарной оценки качества приводит к довольно сложным выражениям и обычно расчет производится при помощи ЭВМ, либо графоаналитическими методами. Рассмотрим пример: , x kz(1 — d) W (z ) = —----(----) z2 — z (1 + d) + d . Передаточная функция замкнутой системы: Ф (zz ,0 )= W(z ,0)=__________kz(1 — d)______ 1 + W (z) z2— z (1 + d) + d + kz (1 - . При действии на вход системы единичного ступенчатого воздействия установившееся значение выходного состояния системы: lim y [ n ] = Ф (z, 0) = 1. n ^» L J V z==1 Изображение квадратичной суммарной оценки имеет вид Z {I2 (0)}= 7-1 kz (1 - d) z2 - z(1 + d) + d + kz (1 - d) z(z -d) (z -1)(z - d) + kz(1 - d) Вычисление квадратичной суммарной оценки производим в соответствии с [4]: b2= 1; a 2 = 1; b1 — - d; a1 — k (1 - d )-(1 + d); b = 0; a о = d; 7» = bb = 0; a2 _ bo b + b1b2 a bо b2 _ Y1 =---= - d; a2 _ b»2 + b2 + b22 a 0 bob2 + a(b0 b + bb2) a1 bob2, Y 2 —---2--+--3--- — 1 - d + kd ( 1 - d ) . a2 a2 Y0 aa Y1 a1 + a2 0 Y2 ai a0 — (a0 + a2 )(a0Y0 - a2Y2) + a1Y1 (a2 - a0)— 1 - d2 + 2kd a 0 a1 a 2 (a 0 - a 2)(a 0 - a1 + a 2)(a 0 + a1 + a 2) k (1 - d )[2 (1 + d)-k (1 - d)] a1 a0+ a2 0 a2 a1 a0 Как следует из приведенного примера, непосредственное вычисление квадратичных суммарных оценок даже для простейших систем приводит к довольно трудоемким операциям, и более целесообразным является использование дискретного аналога теоремы Парсеваля [4]. В этом случае I2 (0) = 517 ^ Y2 (z)' Y (^ )dz ’ 2n j |z|—1 z переходя к W-преобразованию, получим: w 12 —Z( У уст n—0 1 + w z—1—; 1 - w - Г П 2 1 f у[n]) — - J П IV - j dz — 2dw (1 - w )2 Y (w) Y (-w) • 1 + w 1 - w dw ; Y ( z )— Ь2 z 2 + b1 z ; a2z2+ a1 z + a0 Y (w)— C1 w + C0 C1 — b2- b1 — 1 + d; C0— b2+ b1 — 1 - d; d2— a2- a1 + a 0 — 2 (1 + d)- k (1 - d); d1 — 2 (a2- a0) — 2 (1 - d); d0— a2+ a1 + a0— k (1 - d). 1 j'fY(w) Y(-w) 1 jfc(w) c(-w) 12 — -L^.-()dw — 2 -L^-.-()dw n j J. 1 + w 1 - w 2n j v d + w d - w - j f - j f _ c1 d 0 + c 0 d2 _ 1 - d2+ 2 kd — 2 d 0 d 1 d 2 — k (1 - d )[2 (1 + d)-K (1 - d)]. Рис. 6 Нахождение системы на границе устойчивости будет соответствовать 12 = да, откуда легко получаются выражения для границ устойчивости: K > 0; 1 - d > 0; k< 21+d. 1 - d Используя выражение (16), можно в плоскости случайных параметров Kˆ и Tˆ построить, следуя методике [1], линии равных значений и оценить вероятность выполнения рассматриваемой квадратичной суммарной оценки, как показано на рис. 6. Как следует из приведенных примеров, границы устойчивости импульсных систем являются трансцендентными функциями своих параметров, и точное аналитическое выражение вероятности выполнения условий устойчивости для импульсных систем регулирования может быть выполнено при помощи ЭВМ. При предварительном анализе СИР многие из них могут быть сведены к системам второго или третьего порядка, поэтому наличие областей устойчивости для простейших импульсных систем дает возможность разработчику оценить влияние случайного разброса параметров на устойчи- вость системы регулирования. Для ряда систем приближенные выражения приведены в таблице.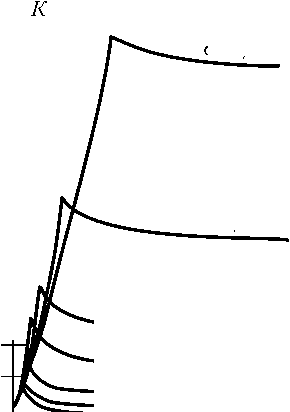

Список литературы Определение вероятности устойчивости систем импульсного регулирования по методу Г. С. Черноруцкого
- Черноруцкий, Г.С. Анализ устойчивости автоматических систем со случайными параметрами/Г.С. Черноруцкий//Известия АН СССР, ОТН «Техническая кибернетика». -1965. -№ 4. -С. 9-16.
- Смирнов, Ю.С. Развитие метода Г.С. Черноруцкого для вероятности устойчивости импульсной системы/Ю.С Смирнов//Труды НПК «Актуальные проблемы автоматизации и управления». -Челябинск: ЮУрГУ, 2013. -С. 76-81.
- Джури, Э. Импульсные системы автоматического регулирования/Э. Джури. -М.: ГИФМЛ, 1963. -335 с.
- Цыпкин, Я.З. Теория линейных импульсных систем/Я.З. Цыпкин. -М.: ГИФМЛ, 1963. -968 с.
- Макаров, В.В. Об одном подходе к расчету дискретных систем со случайным подбором параметров/В.В. Макаров, Ю.С. Смирнов/Тезисы докладов ВК «Стохастические системы управления». -Челябинск: УДНТП, 1976. -С. 45-47.


