Определение вероятностно-временных характеристик при исследовании свойств нагрузки в вычислительных сетях

DOI:

Studies of load properties in computer networks show that the flow of messages at the input of a subscriber station, hub or network controller serving a multipoint network with a «ring» or «tree» structure often differs from Poisson [1-4]. In this regard, the problem arises of studying the probabilistic-temporal characteristics of network elements, which in terms of queuing are characterized by limited memory and an arbitrary flow of requests at the input of the queuing system (QS) [5-7]. We will assume in the future that message lengths are distributed according to an exponential law. Thus, in accordance with Kendall’s symbolism, this work analyzes a queuing system of the G/M/1/N type.

The approach proposed here is a generalization of Kleinrock's result [6] for the G/M/1 system to the case of a system with memory and limited capacity [7].

MATERIALS AND METHODS

As is known, the direct method for calculating the stationary probabilities of the number of demands in the system at the moment of receipt of requests (which gives the distribution of the queue length) is reduced to solving a system of linear equations of the form r = rP,                                           (1)

where r = [Го,ГрГ2,...] .                                                    (2)

and Р - a matrix whose elements are the probabilities of transition to one step P . he problem of calculating stationary probabilities consists of two stages: determining the transition probabilities P and then calculating the stationary probabilities r ;r ;.....

Let us use the following result of Kleinrock [1]: the stationary probability r of the system G/M/1 being in a state E is determined by the equality of the form

Г к = k с ^k,                                          (3)

where K is a certain constant, the type of which is determined by the type of distribution of the input stream; quantity is the only solution to the equation о = А*(ц — цо)  0< ст <1,                        (4)

where A ^* is the Laplace-Stieltjes transform (LST), the density of distribution of time intervals between the moments of messages entering the service system, and ц is the service parameter.

Thus, for a system with infinite memory, calculating the stationary probabilities of the number of requirements in the system is reduced to determining the value of K and с . The parameter K is easily found from the normalization condition:

О00

Z rk = kZck =1;

k=0k and with a known LST for a specific distribution of the incoming flow, finding the queue length distribution is not difficult.

To generalize Kleinrock's results to the case of a system with arbitrary memory (in the particular case, limited memory), we use the properties of the geometric distribution of the queue length in the system, namely, the fact that limiting the buffer size does not change the type of queue length distribution.

Then it can be argued that

Г к = k c N ,                                              (6)

where K is a parameter for a system with limited memory, and the value is the same as for a G/M/1 system (since the shape of с depends only on the type of incoming stream). Just as in the case of the G/M/1 system, the parameter K is found from the normalization condition

N + 1         N + 1

Z rk = kZcN =1, cn = с- k=0        k=0

From here we can obtain the final expressions:

k =

1 - с

1 - с ^{N +}2

и r k =

(1- с )

1- с ^{N + 2}

* с ^k.

RESULTS AND DISCUSSION

This section presents results that illustrate the proposed method of analysis (for systems of type G/M/1/N), hereinafter called the parameter method [8-10], using the following examples below.

М/М/1/N system

The distribution function of intervals between the moments of receipt of requirements has the form:

A(t) = 1 - e^{- X t};

LS transformation, respectively:

A ' (s)= -A -;                              (9)

s + X

Substituting (9) into equation (4), we obtain the following equation

X ^ст = ------------7’

Ц - ^G + X the only solution which is the value G = у = P ; the other root G =1 is not taken into account since the condition 0< ст <1 is satisfied. Substituting the found value CT into expression (8), we obtain the well-known expression for the stationary probability rk in the

M/M/1/N system:

tJz ^p L„,„‘

^rK    1 — p N.J   ^P •

Е2/М/1/N system

We consider a system whose input is a second-order Erlang flow. Provided that the arrival rates at the first and second stages are equal, respectively, to the values ц and 2 ц, where ц is the service intensity, the LST of function A has the form:

A * (s)=----- ^{2 ц} ------,

• ¹    (s + ц )(s +2 ц )

from where [1] we obtain the cubic equation for G :

о ³ -5о ² +6 о -2=0,

solution, which is also further given in (14), namely

о = 2 - V2.

Substituting (13) into expression (8), we find the stationary probability r in the form:

= (У2 -1)(2-У2)к k     1-(2-V2)N+2  "

The probability of overflow is

₌ (У2 - 1)(2 - У2Г .

per   N * ¹     1 - (2 - -ДГ+

D/М/1/N system

The distribution function of intervals between receipts of requirements has the form [2]:

A(t)= ^

0д < 1;

Л

1,t > -. Л

The LST of the distribution function is correspondingly equal to

-(1- о )

A * (t) = e ^р ,

where р = ^Л/ - loading the system with requirements. Ц

Then, following (4), the following equation is valid:

-(1- о )

о = e р

.

This equation can be solved using an approximate method. It is known that ex =2 (x)k, k=0 k!

then we can assume with sufficient accuracy for engineering calculations that

^Ь+^ + С!^]

p        ’Z-P2

-1

,

limiting itself to the first three terms of the sum.

or

Then

Г                 о 1 -1

1 — ст   (1 — ст )

^G + ^ст^ +

L Р     ² Р   А

= 1

ст ² — ст (2 Р + 1) + 2 Р ² = 0

This equation has two roots:

2 р +1+J 4 р —4 р ² +1         2 р +1—д/ 4 р —4 p ² +1

ст 1 =-----------------------;     ст 2 =----------'   -------------

Since 0< ст <1 , then ст ₂ satisfies this condition.

Consequently, the stationary probabilities of the states of the system D/M/1/N will be determined as follows:

P k =

(1— ст ) ст ^k

N+2 1—ст or taking into account the obtained ст we have:

Pk =

(1—2 p + д/ 4 p —4 p ² +1 )(2 p +1—д/4 p —4 р ² +1)^k

,                  I -------------------------1 N+2

2^{k — N — 1}

2    N+2—2p +1—V4 p —4p +1)

g/M/1/N system

Using the method for finding probabilistic-time characteristics outlined above, we obtain probabilistic-time characteristics for a single-channel QS of type g/M/1/N.

For this system, the distribution function of intervals between the moments of receipt of requirements is subject to a geometric law.

Тint=lτ; l=1,2,3, …, where τ – quantum of time, and for l the dependence is valid:

P(l)=b(1-^¹"¹ = p.q ^-1 .                   (15)

The LST of the distribution function is determined by the formula:

-nC1-")

А'⁽P ^- M")= ^P'^e p_{fl aV}                           ⁽¹⁶⁾

1-qe-PC1-ff)

Then, following (4), the following equation is valid:

a =

—^Л(1 — ") р-е ^р

р

1-qe-p(1-ff)

^л(1-") е^р

;

-q

o(_e ?(¹-") -_q) = p.

This equation can be solved by an approximate method, since

∞

ZXk й’ k=0

then we can assume with sufficient accuracy for engineering calculations that

p ^{(1 —a)}   P^{2 (1 —a)} 2

• о 1 +---1-- ~—э--q = p;

P         2p ²

p(1 - o)  p2(1 - 0)2

a 1+-----+--—--^(1-p) =p

P          ²P ²

a  pa(1 — a)

• P^С1-a)(^1-P^-ЦpH) = o•

the solution σ=1 is not suitable, since the condition 0 < σ < 1 must be met, then pa2 — (2p + p)a + 2p2 = 0.

This equation has two roots:

2р+р-7(2р+р)²-8рр²        2р+р+^(2р+р)²-8рр²

Oi =-------^:----------------; a₇ =-------^:----------------.

¹              2p              ²              2p

Since 0 < σ < 1, then σ 1 satisfies this condition.

Consequently, the stationary probabilities of the system states g/M/1/N will be determined as follows:

(1-£)£^

^k     1-_CT N+>

(р-2р+7(2р+р)2-8рр2)(2р+р-7(2р+р)2-8рр2)

(2р)к-"-1-[(2р)"+2-(2р+р-7(2р+р)2-8рр2)"+2]

When p=0, the stationary probabilities of the g/M/1/N system coincide with the stationary probabilities obtained for the M/M/1/N system, and when p=1, for the D/M/1/N system.

Figure 1 shows P k graphs for QS g/M/1/N at ρ=0.7 and 0.9 and p=0, 0.5 and 1.

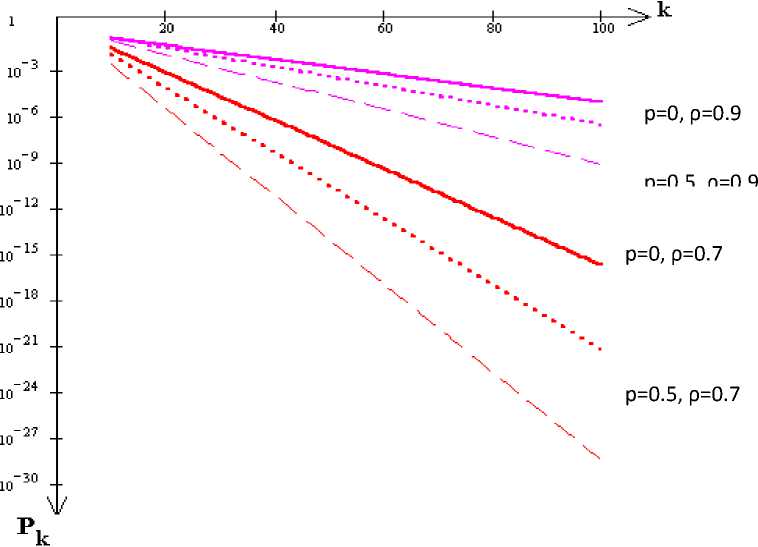
Figure 1. Dependence of stationary probabilities on k for N=100.

CONCLUSION

Thus, determining the probabilistic-time characteristics of a single-line queuing system with a geometric input flow and an exponential distribution of service time with a limited queue (g/M/1/N) allows one to study the properties of the load in computer networks. The application of the method is illustrated on such types of QS as M/M/1/N, E2/M/1/N, D/M/1/N and g/M/1/N. The presented graph illustrates the dependence of stationary probabilities for the QS g/M/1/N at ρ=0.7 and 0.9 and p=0, 0.5 and 1.