Определение вида "упругой" составляющей уравнений состояния молекулярных кристаллов

При построении математических моделей, описывающих быстропротекающие процессы в твердых взрывчатых веществах (ВВ), особую проблему представляют замыкающие соотношения уравнений математической физики - уравнения состояния. В настоящее время для определения параметров уравнений состояния при высоких давлениях и температурах широкое распространение получили двучленные уравнения состояния, в которых внутренняя энергия и давление представляются в виде суммы тепловой и холодной составляющих [1, 2]. Холодные составляющие внутренней энергии и давления не зависят от температуры и определяются только изменением расстояний между молекулами, в то время как тепловая составляющая описывает движение отдельных атомов и молекул в целом. Все твердые ВВ относятся к молекулярным кристаллам нитросоединений, молекулы которых имеют большое число степеней свободы. Межмолекулярное взаимодействие в молекулярных кристаллах органических соединений описывается силами Ван-дер-Ваальса. Построение уравнений состояния молекулярным кристаллов нитросоединений осложняется не только тем, что молекулы имеют большое число степеней свободы, но и тем, что в кристаллах могут образовываться водородные связи, которые уже не описываются только взаимодействием Ван-дер-Ваальса.

Анализ структур органических молекулярных кристаллов показал, что молекулы в органическом молекулярном кристалле образуют плотные упаковки, когда каждый атом молекулы стремится расположиться как можно ближе к атомам соседней молекулы [3]. Принцип плотной упаковки позволил А.И. Китайгородскому [3] сформулировать идею аддитивности энергии взаимодействия как для взаимодействия молекулы с молекулой, так и для взаимодействия атома с атомом в виде модели атом-атомных потенциалов: энергия взаимодействия молекул равна сумме энергий взаимодействий атомов, составляющих молекулы. Эти потенциалы универсальны и зависят только от сорта атома. Для схемы атом-атомных потенциалов могут быть приняты различные аналитические выражения типа (6-ехр-Букингэма) или (6-12-Леннард-Джонса), произвольные параметры которых должны определяться из экспериментальных значений теплоты сублимации простых органических молекулярных кристаллов. В соответствии с моделью атом-атомных потенциалов энергия решетки молекулярного кристалла представляется суммой электростатических и Ван-дер-Ваальсовых взаимодействий в виде

U = E^вв + E^ЭЛ

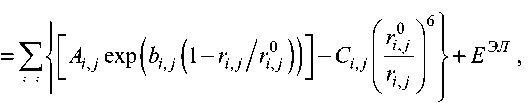
, j exp ( bi, j ( 1 ^- ri, j/r- j

Ci, j r ;

V i , j 7

+ E ЭЛ i, j

где A i j , b i j , rp j , C i j - параметры потенциала Букингема для атомов i и j ; r j - расстояние между атомов г и j ; U - энергия решетки молекулярного кристалла; Е - энергия невалентных Ван-дер-Ваальсовых взаимодействий; E^эл - электростатическая энергия. Энергия электростатического взаимодействия определяется наличием остаточных электрических зарядов на атомах, входящих в состав молекул.

Несмотря на широкое применение двучленных уравнений состояния, остается еще много вопросов, связанных как с формой, так и с содержанием тепловой и холодной составляющих уравнений состояния. Поэтому цели настоящего исследования можно сформулировать следующим образом:

• 1.    Определение вклада энергии электростатических взаимодействий в энергию решетки молекулярного кристалла нитросоединения;

• 2.    Выбор потенциала межмолекулярного взаимодействия, адекватно описывающего структуру взаимодействий в молекулярном кристалле нитросоединения;

• 3.    Обоснование выбора формы потенциала межмолекулярного взаимодействия, замыкающейся на известные экспериментальные данные.

Оценка вклада электростатических взаимодействий в энергию решетки молекулярного кристалла

Модель атом-атомных потенциалов успешно применялась А.И. Китайгородским с сотрудниками для исследования свойств органических молекулярных кристаллов. Было показано, что энергия электростатических взаимодействий пренебрежимо мала по сравнению с теплотой сублимации (энергией решетки) для таких веществ, как углеводороды даже в случае молекул с большими дипольными моментами и ее можно не включать в схему атом - атомных потенциалов при проведении расчетов энергии решетки [3].

Последнее утверждение не является очевидным особенно для молекулярных кристаллов нитросоединений. Во-первых, заряды на атомах молекул нитросоединений на порядок больше зарядов на атомах обычных органических соединений, во-вторых, кристаллы нитросоединений содержат сильные водородные связи. Поэтому вопрос выбора модели атом-атомных потенциалов может быть решен только с помощью прямых расчетов энергии решетки молекулярных кристаллов нитросоединений, включающей в себя энергию Ван-дер-Ваальса и энергию электростатических взаимодействий.

Аналогично работе [4] проведем оценку вклада энергии электростатических взаимодействий в энергию решетки ряда молекулярных кристаллов нитросоединений. В качестве объектов исследования были выбраны молекулярные кристаллы нитробензола, р-динитробензола, т-динитробензола, р-нитротолуола, гексогена, р-нитроанилина, 2,4,6-тринитроанилина, 1,3,5-триамино-2,4,6-тринитробензола. Данный набор молекулярных кристаллов нитросоединений был выбран не случайно: в литературе для них имеются экспериментальные данные по теплоте сублимации и данные ренгеноструктурного анализа [4]. Для увеличения достоверности вычисления энергии электростатического взаимодействия заряды на атомах молекул нитросоединений рассчитывались в конформациях (геометрии), выбранных на основе данных ренгеноструктурного анализа, то есть соответствующих конформации молекул в кристалле. Эффективные заряды на атомах, воспроизводящие электростатический потенциал в окрестности молекулы и входящие в состав молекул перечисленных выше нитросоединений, вычислены в приближении Хартри-Фока более современными квантово-химическими методами [5], нежели это было сделано ранее в работе [4]. При вычислении энергии электростатических взаимодействий были использованы разные модификации метода Эвальда [6, 7].

Потенциалы невалентных взаимодействий Е^в - ^в , определяющие взаимодействие Ван-дер-Ваальса, описывались универсальной кривой для каждого сорта атомов i и к в форме потенциала (6-ехр-Букингэма) [3, 4, 8].

Результаты расчетов энергии решетки молекулярных кристаллов нитросоединений и энергии электростатических взаимодействий приведены в таблице. Анализ приведенных результатов расчетов показывает, что вклад энергии электростатических взаимодействий в энергию решетки (те- плоту сублимации) молекулярных кристаллов нитросоединений является значительным, в отличие от чисто органических молекулярных кристаллов, и может достигать 20-25 % энергии решетки. Поэтому при расчетах термодинамических характеристик молекулярных кристаллов нитросоединений, необходимых для построения уравнений состояния, должна быть использована полная схема атом-атомных потенциалов [3], то есть обязательно должна включаться в расчет энергия электростатических взаимодействий.

Сравнение экспериментальных и вычисленных энергий решетки

Соединение	ТТЭКСЛ 11 субл ( Т = 298 К)	ттЭКСЛ 11 субл ( T = 0 К)	и выч 11 субл ( Т = 0 К)	E эл
	Ккал /моль
Нитробензол	13,98	15,14	15,30	2,7
т-динитробензол	19,40	20,57	20,60	6,5
р-динитробензол	21,20	22,37	22,50	5,9
р-нитротолуол	18,90	20,07	20,30	4,5
Гексоген	31,11	32,34	31,29	7,6
р - нитроанилин	24,10	25,20	25,30	6,9
Тринитроанилин	27,71	28,80	28,20	7,5
1,3,5- триамино- 2,4,6-тринитробензол	40,21	41,30	40,20	8,4

Определение формы упругой составляющей уравнений состояния молекулярных кристаллов

Вычисление упругих (невалентных межмолекулярных) составляющих внутренней энергии с учетом строения кристаллической решетки, проведенное в ряде работ [3, 4], показывает, что подобная детализация расчетов приводит к огромным затратам машинного времени, а аппроксимация энергии невалентных межмолекулярных взаимодействий U_y набором потенциалов в модели А.И. Китайгородского приводит к появлению большого количества констант, которые не всегда удается адекватно определить из имеющихся экспериментальных данных.

Следовательно, целесообразно подобрать некоторый эффективный потенциал упругого взаимодействия, который бы учитывал и особенности, полученные в результате детальных расчетов энергии упругих взаимодействий молекулярных кристаллов нитросоединений, и мог быть использован при решении задач математической физики.

Учитывая все выше сказанное, для энергии упругих взаимодействий U_y , в соответствии представлениями работы [5], должно быть принято следующее выражение:

Uy (x) = ^A- exp Гb (1 - x13)! - C-x“2 - —x4/3, (1) bpo L V 7J 2po Po где x = p0 /p - безразмерный объем; A, b, C , D - постоянные подлежащие определению. Второй и третий члены выражения (1) описывают энергию притяжения. Сравнивая вычисленную энергию решетки кристалла с его теплотой сублимации, видим их различие как раз в энергии притяжения. Это может объясняться недостаточным учетом энергии водородных связей, существующих в молекулярных кристаллах нитросоединений. Поэтому целесообразно модифицировать потенциал упругих взаимодействий (1). В силу того, что выражения, описывающие энергию притяжения в потенциале упругих взаимодействий (1), имеют минимум для x = 1, имеет смысл заменить сумму второго и третьего членов в выражении (1) одной функцией следующим образом:

U_y = — exp Г b (1 - x ^1/3 Я — —x~n . (2) ^y b p o ^PL ⁽ ) J n p o ^v

Потенциалы упругих взаимодействий (1) и (2) различаются тем, что показатель степени в выражении, описывающем энергию притяжения, не является фиксированным и подлежит определению из экспериментальных данных [9, 10]. Для определения констант, входящих в выражение (2), необходимо из эксперимента выбрать четыре параметра и замкнуть на них уравнения состояния при температуре T = 0.

Найдем связь между упругими составляющими внутренней энергии и давления. Известно, что термодинамические свойства вещества полностью определяются, если известен один из термодинамических потенциалов. Для молекулярных кристаллов удобно исходить из определения свободной энергии Гельмгольца F(V, T), которая наиболее простым образом связана с моделью строения вещества:

F = U_y + E о + kT l in 1 1 — exp ( — h ^a- I] , E о = ¹ l H to_a .                 (³⁾

a I V ^kT ))      ² а

Здесь U_y - энергия взаимодействия между атомами; V - удельный объем; T - температура тела; к - постоянная Планка; го_а - частоты нормальных колебаний; E ₀ - энергия нулевых колебаний. Если предположить, следуя работам [11, 12], возможность использования для низкочастотной составляющей свободной энергии подхода Дебая, а для высокочастотной - подхода Эйнштейна, то выражение (3) перепишется в виде

I    MT

F = Uy + E _o + 3 MRT —       ^ 2 in ( 1 - exp ( - £ ) ) d ^ + ( 3 N - M ) RT in 1 - exp I — ^E I ,   (4)

0         V 9 d J о                                       V V T ))

где R - универсальная газовая постоянная; M - число низкочастотных колебаний; N - число атомов в молекуле; 3N - M - число высокочастотных колебаний; 0D - характеристическая тем пература Дебая; 0E - характеристическая температура Эйнштейна. Зная выражение для энергии

Гельмгольца, легко определить вид уравнения состояния молекулярного кристалла и теплоемкости при постоянном объеме:

dUy dEо mrtYd (V)D ( Xd ) у, „X   d (h »D).,„

• P.... " dT +         V ■ Yd (V )=-■d(inV)’ -

• E = F + TS = Uy + E0 + MRTD (xD) + (3 N - M)---—E ;(6)

exp ( ^X e )^{- 1}

Cv = MR f 4D (Xd )--3xD—1 + (3N - M) Rx   ^p''),(7)

V            exp ^{( X} d ^{) - 1 1}                 ( exp ( x_E ) - 1 )2

где x_D = 0 _DIT , x_E = 0 _EIT , y _d (V ) - коэффициент Грюнайзена. В работах [11, 12] подробно описан алгоритм определения числа низкочастотных колебаний молекулярных кристаллов нитросоединений. Следуя определению коэффициента Грюнайзена [13], получим выражения для энергии нулевых колебаний E 0 и ее производной -^0-:

^E 0 = ^L ^{Н ю} а =

² а

3 N '- M'

-------^{к ю} _а

+ 3 M D ^ „^ = 3 N-M R ^ + 3 MR ^ ( V )

2 ₀                2 ^E 8 ^D

dE 0_ 3 MR Y d ( V )9p ( V )

^^^^^^^^^^^^^^^^^^^^^^^^^B               ^^^^^^^B ^^^^^^^B ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^B dV 8 V

где N' - число атомов, M' - число низкочастотных колебаний в объеме V . Подставляя выражение для производной от энергии нулевых колебаний по объему (9) в выражение для давления, получаем уравнение состояния в виде р = MTyD(V)d(xd) + р0 + py , р0 = 3 MRyD (v)@п^; py =-dU .        (W)

V                       8                     dV

В соответствии с соотношением (2) получим выражение упругого давления P_y , обусловленного энергией упругих взаимодействий U_y ( x ), в следующем виде

—2

(

P_y _ Ax ³ exp b 1 — x L I

1M

— Cx ^{— ( n + 1)}.

Для получения более понятных с точки зрения физики выражений упругих составляющих внутренней энергии (2) и давления (11) сделаем ряд преобразований. По определению, изотермическая сжимаемость P T связана с изотермической скоростью звука c_T следующим образом:

1 _cT_ Л д P ) — V

.

P _T  V     (д V J _T

Подставляя выражение (10) в правую часть равенства (12), в результате получим

Pt

— I

^V ^1 MRT Y D ^{( V} )^{[ 3 x} D ⁺ D

_— ^V J — MRT Y D ( ^V ) у Xd + D

+ MRT Y D ( ^V ) - Xd + 8

^{V +} P y I

) T

^{V 2} + MRT Y D '( ^V ) 3 xd + D

D X x_D )1 ^ xD/v + — 1 ^{( D} ) ] д v/     d v J.

T

_— ^v J— MRT Y D ( ^V ) - Xd + ^D

V +

V ² +

, в в 3

+ MRT Y D ( ^V ) _s Xd + D 8

( Xd )1 / V — MRT Y D ( V ) Г 3 -I                      L 8

xD

— CVD (xD ) + D

_ MRT [ Y > ( V ) + Y d ( V ) ]

— x + D 8 ^D

V — V ^Pr- — MRT y D ( V ) Cv_d ( Xd )/ V — д V                 ^D

—

■ ^mrt / d ( ^v ) - Xd + ^D ( xd ) ,

где y D (V ) - производная по V от коэффициента Грюнайзена,

^C V_D ⁽ x D ^)_ I ^{4 D (} x D )

^^^^^^^в

3y A

3 x_D

^{д x} D _

exp ( x_D ) — 1 J ’ д V

— V Y d ( V ) .

Следовательно, выражение для определения изотермической сжимаемости можно записать следующим образом

• 1 - _ MRT [ y d ( V ) + Y d ( V ) ] P t

• -    x_n + D 8 ^D

^^^^^^^в

• — MRTyD (V) Cvd (Xd )/

, в вГЗ          в в1

• ^V    — MRT / D ( ^V ) 8 xd + ^D ( xd ) — ^V-V ,

Проведем оценку членов, входящих в выражение для внутренней энергии (6), при стремлении температуры T к нулю. В этом случае речь идет о низкотемпературном пределе T ^ 0, xD ^^ , xE ^7 . Низкотемпературный предел для функции Дебая D (xD) можно получить, если представить интеграл, входящий в ее выражение, в виде xD e   d^   _7e   d^

0     exp ( e ) — 1 0    exp ( e ) — 1

^^^^^^^в

7 _e   d e  _ П 4

_x ^D   exp ( e ) — 1   15

^^^^^^^в

7 e  de xD   exp(e)—1.

При низких температурах T параметр xD велик, так что второй член в последнем равенстве можно оценить, отбросив 1 в знаменателе подинтегрального выражения 7            , с,7

j e ---_ f ^[ e ³ exp ( — e ) l d e _ exp ( — Xd ) ( x D + 3 x D + 6 Xd + б ) .

J    exp(e)—1    JL              ]                   v xDx

Подставляя последнее выражение в функцию Дебая, получим п4               /                      \

D ( X D ) = -3 x

— - exp ( - x_D ) ( x D + 3 x D + 6 x D + 6 )

n 0.

Проведя предельный переход в последнем члене внутренней энергии, получим

®Е exP (xE )-1

________n eE xe >■ exp ( Xe )

Для внутренней энергии E предельный переход к низким температурам можно представить следующим образом

3 N - M}RTx_F

E = U + E0 + MRTD (xD) + 3-----E = exp ( xe )-1

= U + Eo + MRT— xD L15

- exp ( - x D ) ( x D + 3 x D + 6 x D + 6

+

( 3 N - M ) R ^e

⁺------;—;--ⁿ U ^{(1) + E} o .

exp ( x_E )       x e >■

Энергия нулевых колебаний E ₀ определена выражением (8). Для определения изотермической сжимаемости при T n 0, переходим в выражении (13) к пределу следующих функций:

Tini MRpT[yd (V) + yd (V)]3xD = 3 eDMRp[yd (V) + yd (V)], lim MRpT[yd (V) + yd (V)]D(xD ) = 0, lim MRpTyd (V) Cvd (xD ) = 0, lim MRT yd '(V)3 xD = 3 MReDYD'(V),

T n0              88

lim MRT y d ‘ ( V ) D ( x D ) = 0.

Следовательно, при T n 0 изотермическая сжимаемость определяется следующим выражением

I1

v P t ) t n0

= 3eDMRpFyD (V) + yd (V)1 -3MReDYD'(V)-VP(15)

8 L                J 8d

Переходя в (15) от изотермической сжимаемости к изотермической скорости звука в соответствии с формулой (12), получим

• V=3 eDMRp [yd (v)+YD (V)] - 3 MReDYD'( v )-v |V,(16)

где c 0 - скорость звука при T = 0 .

Полагая далее, что скорость звука при T = 0 определяется только упругими свойствами кристаллов, получим два уравнения:

4 =

V 0

^^^^^^^e

у P

⁰ dV ,

Y D ' ( ^V 0 )^-    Y D ( ^V 0 )^- V Y D ( ^V 0 ) = 0.

• V ₀           V ₀

Подставляя в правую часть равенства (17) выражение для холодного давления (11), получим при x = 1

• - у ^ P L = -3 5 1 = - ² Ax -^5/3exp Г b (1 - x ^1/3 Я - ³ Abx ~^4/3exp F b (1 - x ^1/3 Я +

⁰ d v      d x     3 ^p L ⁽         ) j 3            ^p L ⁽         ) j

+ C ( n + 1 ) x ⁽ n ^{+ 2 )} =- ² A - ¹ Ab + C ( n + 1 ) .

В силу того, что для x = 1 упругая составляющая внутренней энергии имеет минимум, то величина упругой составляющей давления равна нулю при x = 1, и, как следует из выражения (11), коэффициенты A и C равны. Из равенств (17) и (18) можно определить выражение для коэффициента A через скорость звука c 0 для x = 1 и T = 0 :

A = 3 c 2 Р о / ( b - 3 n - 1 )

В этом случае выражения для упругой составляющей внутренней энергии и упругой составляющей давления принимают следующий вид:

3 c ²

U y = к /к 1 й ³ n exp ( b ( 1 ^- x ) ) ^- bx                          ⁽¹⁹⁾

bn ( b - 3 n - 1 ) L       ' '        '' J

P y =

^{3 c} 0 ^p 0

bn ( b - 3 n - 1 )

-2/3

exp ( b ( 1 - x ^1/3 ) )

x ^{- n + 1 )}

Выводы

• 1.    При проведении расчетов по определению энергии решетки молекулярных кристаллов нитросоединений необходимо применять полную схему атом-атомных потенциалов.

• 2.    В работе получены выражения для упругой составляющей внутренней энергии (19) и упругой составляющей давления (20), которые наиболее простым образом определяются из известных экспериментальных данных.

• 3.    Коэффициенты n и b в выражениях (19) и (20) определяются по экспериментальным ударным адиабатам молекулярных кристаллов.