Определение выражения изобарического коэффициента объемного расширения для некоторых молекулярных кристаллов нитросоединений

Построение уравнений состояния в широком диапазоне давлений является необходимым элементом для математического моделирования нестационарных газодинамических процессов импульсного воздействия на вещество [1–2]. Это связано с тем, что в основе математических моделей механики сплошных сред, термодинамики, электродинамики и т. д. лежат законы сохранения массы, импульса и энергии, которые не являются замкнутой системой и требуется определить зависимости между входящими в уравнения сохранения величинами [3–4].

Уравнения состояния определяют фундаментальную связь между термодинамическими параметрами вещества, не зависящую от способа достижения тех или иных значений этих параметров. Математические модели термодинамических свойств вещества постоянно совершенствуются. Для анализа и проверки адекватности предлагаемых математических моделей требуется наличие экспериментальных данных в широком диапазоне температур и давлений.

Применение строгих теоретических методов расчета термодинамических свойств материалов даже в ограниченных интервалах термодинамических параметров не всегда позволяет получать достоверные результаты. В этой ситуации особое значение приобретают методы построения полуэмпирических уравнений состояния [5]. В данном случае вид функциональных зависимостей термодинамического потенциала для полуэмпирического описания определяется из теоретических соображений, а результаты экспериментов используются для определения входящих в эти зависимости коэффициентов. Несмотря на то, что решению задачи построения уравнений состояния молекулярных кристаллов посвящено достаточно большое количество как экспериментальных, так и теоретических работ, теория построения уравнений состояния молекулярных кристаллов иитросоединений далека от своего завершения [1, 6, 7]. Это связано с тем, что с одной стороны теоретическое определение зависимостей, характеризующих поведение твердых взрывчатых веществ (ВВ), которые относятся к молекулярным кристаллам, осложняется большим числом внутренних степеней свободы молекул, входящих в состав молекулярного кристалла нитросоединений, а с другой стороны проведение экспериментальных работ ограничены требованиями безопасности.

Известно, что термодинамические свойства вещества полностью определяются, если известен один из термодинамических потенциалов. Для твердых тел удобно исходить из определения свободной энергии Гельмгольца F ( V , T ) , которая наиболее простым образом связана с моделью строения вещества [6–8]:

F = U + E о + kT £ ln(1 - exp( - h^ )), E о = ¹ £ h to_a . (1) a ^{kT 2} a

Здесь U – энергия взаимодействия между атомами; V – удельный объем; T – температура тела; h - постоянная Планка; k - постоянная Больцмана; to_a - частоты нормальных колебаний; E ₀ -энергия нулевых колебаний. Суммирование в формуле (1) производится как по частотам колебаний молекул, образующих кристалл, так и по частотам колебаний атомов, входящих в состав молекул.

Если известен вид функции свободной энергии Гельмгольца F ( V , T ) и определены все значения параметров, входящих в описание функции F ( V , T ) , то дифференцированием могут быть найдены выражения для определения всех измеряемых и вычисляемых термодинамических величин [9].

В настоящее время принято считать, что в уравнения состояния молекулярных кристаллов входят две составляющие: тепловая и «холодная» [1, 5, 10, 11]. Тепловая составляющая определяется колебательным движением молекул, входящих в состав кристалла, а холодная составляющая – изменением энергии взаимодействия, как внутри молекулы, так и между молекулами, входящих в состав кристалла, в зависимости от объема. Для получения достоверных результатов необходима независимая верификация тепловой и «холодной» составляющих уравнения состояния по известным экспериментальным данным. Для тепловой составляющей уравнения состояния это могут быть экспериментальные данные по зависимости теплоёмкости и объема элементарной ячейки молекулярного кристалла от температуры.

Целями настоящего исследования являются:

• 1.    Получение функциональной зависимости изобарического коэффициента объемного расширения молекулярного кристалла от температуры.

• 2.    Верификация полученной зависимости изобарического коэффициента объемного расширения от температуры по экспериментальным данным для 1,3,5 – 2,4,6 – тринитробензола (ТАТБ).

Уравнения состояния молекулярных кристаллов нитросоединений для описания зависимости изобарического коэффициента объемного расширения от температуры

Известно, что энергия взаимодействия между атомами молекулярного кристалла складывается из внутримолекулярной и межмолекулярной. Внутримолекулярная энергия определяется энергией валентных взаимодействий атомов внутри молекулы. Межмолекулярная энергия является энергией не валентных взаимодействий атомов между молекулами. Если

Ковалев Ю.М.               Определение выражения изобарического коэффициента объемного расширения для некоторых молекулярных кристаллов нитросоединений межмолекулярная (кристаллическая) энергия UC зависит от пространственного расположения молекул, т. е. от объема, то внутримолекулярная энергия UM зависит исключительно от величины валентных связей и валентных углов. Поэтому целесообразно разбиение энергии взаимодействия между атомами U в равенстве (1) на две составляющие: внутримолекулярную энергию UM и межмолекулярную энергию UC .

Все частоты нормальных колебаний в кристалле можно разделить на низкочастотные и высокочастотные. К низкочастотным колебаниям можно отнести шесть колебаний молекулы как целого (три колебания центра масс и три угла Эйлера) а также колебания внутри молекулы, зависящие от кристаллического поля, например торсионные колебания нитрогрупп. В дальнейшем низкочастотные колебания будем называть деформационными (акустическими) . Остальные колебания внутри молекул будем относить к высокочастотным (оптическим) колебаниям. Учитывая тот факт, что высокочастотные колебания внутри молекулы на порядок больше деформационных частот, можно ввести две характеристические температуры и разделить колебательную составляющую свободной энергии на низкочастотную (акустическую) и высокочастотную (оптическую). В силу того, что частоты деформационных колебаний определяются изменением энергии U_C , т. е. энергии невалентных взаимодействий между молекулами, то только эти частоты нормальных колебаний и будут зависеть от объема. Данное предположение было успешно применено в работе [12] для расчета температуры на фронте ударной волны для ряда органических нитросоединений и экспериментально подтверждено в работе [13] для нитрометана.

Предположив возможность использования для низкочастотной составляющей свободной энергии подхода Дебая, а для высокочастотной – подхода Эйнштейна [11, 14], перепишем выражение (1) в виде

9 d f T

F = U + U + E + 3MRT — J ^2ln (1 - exp (-£)) d^ + (3N - M) RTIn 1 - exp -— , (2) C M 0        ( 6d j 0                                      < V T J J где R - универсальная газовая постоянная, поделенная на молекулярную массу вещества ц; M - число низкочастотных (деформационных) колебаний; N - число атомов в молекуле; 3N - M -число высокочастотных колебаний; 6D - характеристическая температура Дебая; 0E - характеристическая температура Эйнштейна.

Интегрируя по частям выражение для низкочастотной составляющей свободной энергии F ( V , T ) , определенное равенством (2), и вводя функцию Дебая D ( x ) [15]

x d< exP (£)-1 ,

D ( x ) = -3 3- J £ x ₀

получаем

• f                    D(x_n 1Л

F = U + U + MR— ln ( 1 - exp ( - x ))-- + ( 3 N - M ) RT In ( 1 - exp ( - x_E ) ) ,

V                       3 j где xD =—; xE = T.

Используя выражение (3), легко получить выражения для давления P и энтропии S :

P = -f № Л =-« U c -« U M - dE 0 - MRTD ( x_D ) d fln f D ) 1 -

Vd V ) _T d V d V dV D ^Dd d ( In V ) V

- ( 3 N - M ) RTx E

d ( In d _E )          1         ;

d ( In V ) V ( exp ( x_E ) - 1 ) ;

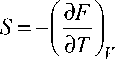
MR P ln(1 - exp( - x_D ))- D ( x D l 1 + MRT Г exp⁽, xD ). - D ’ ^ x D ^ 1 ^ x D l L ^{(        (} D ) ) 3 J        [ 1 - exp ( - x D )       3 J d T

+ ( 3 N - M ) R ln ( 1 - exp ( - x_E ) ) + ( 3 N - M ) RT

exp ( - X e ) d x_E

1 - exp ( x_E ) d T

-

MR In ( 1 - exp ( - x

-

D ( xD )

-

- MRD ( x_D ) + ( 3 N - M ) R In ( 1 - exp ( - x_E ) ) - ( 3 N - M )

RTxE

exp ( X e ) - 1

При выводе формулы (5) было использовано свойство функции Дебая

D(x) =---XVa -xD'(x), exp (x)-1 3

где штрих обозначает дифференцирование по характеристической температуре x .

Зная равенства (3) и (5), легко определить выражения для полной энергии E и теплоемкости при постоянном объеме C_V :

E = F + TS = U_C + U_M + E 0 + MRTD ( x_D ) + ( 3 N - M )--- , ^E_x ;

exp(Xe - 1)

C_v = MR 4 D ( x_D )

V

3 X d exp ( x D )^{- 1} _v

exp x

+ ( 3 N - M ) RxE ---- ^{P V E} )   = C vd + C vm .

( exp ( xE )- 1)

Здесь C_VD – составляющая теплоёмкости при постоянном объёме, зависящая от деформационных (акустических) колебаний молекулы и определяемая в приближении Дебая, а C_VM – составляющая теплоёмкости при постоянном объёме, зависящая от внутримолекулярных (оптических) колебаний. Часть теплоемкости C_VM называют внутримолекулярной.

Следуя определению коэффициента Грюнайзена

Y (V) = _d(ln6» )YD ( )     d (ln V) , выражение (4) можно записать в виде p =

d U c d U_M

d V d V   dV

dE о + MRT Y d ( V ) D ( X d )

V

Последний член в выражении (4) равен нулю, так как при разделении частот было сделано предположение о независимости высоких частот от объема.

Исходя из определения энергии нулевых колебаний и учитывая разделение частот, получаем dE выражения для функций E0 и dV0 :

^E 0    ^ h ® a

² a

3 N '- M '_ 3 M ‘ w D 2, , 3 N - M      3_WDa ,_TA

---2 hw_E +     J w ² hwdw = 2 R ^ E + 8 MR ° D ( v ) ;

dE ₀ dV

3 MR Y d ( V ) 9_D ( V )

V

,

где N' - число атомов, M' - число низкочастотных колебаний в объеме V .

Подставляя выражение для производной от энергии нулевых колебаний по объему (7) в равенство (6), получаем уравнение для определения давления в виде

MRTy ( V)^     ,

P =---- D 1- X d + D ( X d ) 1 + P e , P e =

V V 8              7

dU_C dV_M

dV dV

Как было показано в работах [16, 17] зависимость коэффициента Грюнайзена от плотности описывается выражением следующего вида:

V

Yd = C - V ’ где константа C определяется из условия yD (V0 ) = YD- Здесь YD значение коэффициента Грю- найзена при нормальных условиях V = V0, T = T0. Похожее выражение для коэффициента Грю- найзена было получено из других соображений в работах А.М. Молодца [18, 19]. В результате получим

Y d = y D

( V ]— ^{V 0} ) 1 ₊ y D

1 -

V

Формула (9) в случае слабого сжатия переходит в известное эмпирическое выражение

V v У

которое широко используется при обработке экспериментальных данных.

Для того чтобы воспользоваться выражением для коэффициента Грюнайзена y d (9), необходимо определить его значение y D , соответствующее начальному удельному объему V _o. С этой целью в работе [20] был получен аналог уравнения Грюнайзена для молекулярных

кристаллов в виде:

^{а С}т 2 = ^Y d ( ^V ) c vd

Следовательно, если из эксперимента известны значения изобарического коэффициента объемного расширения а , изотермической скорости звука с _т и определен способ нахождения

теплоемкости при постоянном объеме C _VD , из уравнения (10) можно найти значение

коэффициента Грюнайзена Y d при начальном значении удельного объема и температуры. Это

даст возможность использовать выражение (9) для определения зависимости коэффициента Грюнайзена молекулярных кристаллов от удельного объема, а выражение (10) для определения зависимости изобарического коэффициента объемного расширения а от температуры.

Известно [6, 8], что характеристическая температура Дебая для акустических колебаний

молекулы при нормальных условиях в случае молекулярных кристаллов нитросоединений может

быть определена, если существуют экспериментальные данные по значениям теплоемкости при постоянном объеме или данные по значениям продольной и поперечной скоростям упругих волн

молекулярных кристаллов нитросоединений. В силу того что экспериментальные данные по теплоемкости при постоянном объеме определены в некотором диапазоне значений [20], достоверно определить значение характеристической температуры Дебая не представляется

возможным [21].

В модели Дебая [4, 6] реальный спектр акустических колебаний атомов заменён простой

зависимостью. Максимальная частота колебаний для молекулярных кристаллов зависит от объёма и физических свойств вещества и определяется по формуле [4]

® D

= C s

( MN a P f³,

V 4 пи ) ,

где N_a – число Авагадро, C_S – средняя скорость звука, выражаемая через скорости продольных

C_L и поперечных C_t упругих волн в кристалле

³ С_S

г

2 )

—Г +—г с3 с³ V C L C t )

Максимальная частота to _D определяет характеристическую температуру Дебая

6 d = h ^ D . (13) k

В силу того, что уравнения состояния определяют шаровую часть тензора напряжений, то в равенстве (12) необходимо перейти от средней скорости звука C_S к адиабатической скорости звука С ₀ , учитывая следующие соотношения:

_{2    2} 4 G ₂ G

CL = C 0 +    , Ct = где G – модуль сдвига. Анализ экспериментальных данных [22] показал, что связь между средней скорости звука CS и адиабатической скоростью звука С0 может быть описана простой зависимостью:

C S = KC 0 , (14) где значение корреляционного коэффициента K для дальнейших расчетов было выбрано равным 0,75.

На примере ТАТБ рассмотрим способ определения количества деформационных колебаний M , максимальной частоты ω _D и характеристической температуры Дебая θ _D . Это связано с тем, что в настоящее время в справочной литературе, представляющей экспериментальные данные по молекулярным кристаллам нитросоединений, только для ТАТБ имеется полный набор экспериментальных данных [22–24], позволяющий определить зависимость коэффициента объемного от температуры. Значение адиабатической скорости звука ТАТБ, определенное по изотермической сжимаемости [24], равно 2350 м/сек, а значение средней скорости звука C S , определенное формулой (14), равно 1762,5 м/сек.

Для определения количества деформационных колебаний M молекулярного кристалла ТАТБ воспользуемся результатами расчетов, приведенных в работе [25]. Силовые постоянные для расчета спектров нормальных колебаний внутри молекулы были определены с помощью квантово-химических методов РМ-3 и DFT, подробно описанных в работах [26, 27]. Полученные в расчетах ИК – спектры для ТАТБ хорошо согласуются с известными экспериментальными данными [28].

Процесс расчета деформационных частот является итерационным. Для молекулярных кристаллов шесть колебаний: три колебания центра тяжести молекулы и три колебания углов Эйлера, определяющих поведение молекулы как целого, однозначно относятся к низкочастотным колебаниям. Следовательно, на первом этапе количество деформационных колебаний M = 6. Сравнивая вычисленные по формуле (11) значения максимальных частот Дебая со значениями внутримолекулярных частот ТАТБ [25], получим, что количество деформационных колебаний M = 12.

Проводя расчет характеристической температуры и частоты Дебая по формуле (14) для M = 12, получим для ТАТБ θ _D = 137,30 K; ω _D = 95,83 см^–1. Полученные значения характеристических температур и частот Дебая показывают, что внутримолекулярные колебания трех нитрогрупп и трех аминогрупп ТАТБ также необходимо включать в число деформационных колебаний, частоты остальных внутримолекулярных колебаний находятся значительно выше полученных значений максимальных частот Дебая.

Определение формы изобарического коэффициента объемного расширения молекулярных кристаллов

Для определения начального значения коэффициента Грюнайзена γ _D ⁰ воспользуемся равенством (10). Подставляя в него значения изотермической скорости звука c _T , изобарического коэффициента объемного расширения α и теплоемкости при постоянном объеме, соответствующей деформационным колебаниям C_VD , получим значение коэффициента Грюнайзена γ _D ⁰ , соответствующее начальному состоянию T = 293 К, V ₀ = 0,5162 см³/г. Для ТАТБ при количестве деформационных колебаний M = 12 коэффициент Грюнайзена γ _D ⁰ равен 1,44.

В силу того, что попытки аппроксимации экспериментальных данных без учета свойств реальных материалов, приводят к неутешительным результатам по определению зависимости изобарического коэффициента объемного расширения от температуры, в настоящей работе был предложен подход, позволивший исправить данную ситуацию.

Рассмотрим уравнение (10), где коэффициент Грюнайзена определяется линейной зависимостью от удельного объема, получим

Г V ^ ^аС т = ^y d ^(v ) c vd , T o = T o 77" .

V V 0 7

В силу того, что изобарический коэффициент объемного расширения определяется термодинамическим равенством

1 ( д V ) a = — — ,

V к д T J P то, подставляя данное выражение в равенство (15), получим следующее дифференциальное уравнение для определения зависимости плотности молекулярного кристалла от температуры

Го А

Y d Р о

P

С ² к C T

C vd (T ) = LURID ( x ).

Здесь были введены следующие обозначения

K a

\ 2

к C T J

x

, D ( x ) = -4 J ^⁴

x ₀

^exP ( £ )^- 1.

Аналитически проинтегрировать по температуре правую часть равенства (16) не представляется возможным. Поэтому в диапазоне температур 153–413 K, в рамках которого были проведены эксперименты [23], функцию теплоемкости Дебая D_C ( x ) [8] достаточно точно описывает высокотемпературное приближение:

D _r ( x ) = 1 - —x ² +— x ⁴.

^C 20    560

Данное выражение уже легко интегрируется по температуре и результатом интегрирования является функция вида

F c ( x ) = J D e ( x ) dT = T (1 + 20 x ²

1 4 x .

Интегрируя уравнение (20) по температуре от значения T ₀ = 293 К до текущего значения T при постоянной изотермической скорости звука, получим равенство, позволяющее определить значение плотности р для произвольной температуры

Р = Р о + K a MRF e ( x )| T 93 .                              (17)

Зная зависимость плотности молекулярного кристалла от температуры, количество молекул в элементарной ячейке Z , молекулярный вес вещества ц , из равенства (17) легко получается выражение для зависимости объема элементарной ячейки кристалла от температуры в виде

V e = Z ■ ц /(N a ■ р ).

В таблице проведены значения экспериментальных V_EX и рассчитанных V р объемов элементарных ячеек для ТАТБ при различных температурах.

Изменение объёма элементарной ячейки кристаллитов ТАТБ при температурном воздействии

T, K	VEX , А³	V C , А³	T, K	VEX , А³	V C , А³
153	435,48	438,38	293	444,39	444,39
173	436,85	439,22	313	444,92	445,50
193	437,27	440,29	333	447,37	446,37
213	438,83	431,15	353	449,28	447,26
233	440,45	442,00	373	451,28	448,15
253	442,26	442,87	393	452,17	449,05
273	443,82	443,74	413	454,37	449,96

Данные таблицы показывают, что рассчитанные и экспериментальные значения объемов элементарных ячеек кристаллов ТАТБ различаются на 2–3 % во всем диапазоне изменения температур. Следовательно, равенство (15) можно применять для аппроксимации коэффициента объемного расширения молекулярных кристаллов нитросоединений. Условие стремления изобарического коэффициента объемного расширения к нулю при стремлении температуры к нулю будет выполняться автоматически.