Определение зависимости усилия в уплотняющем элементе торцевого мембранного уплотнения от общей нагрузки

Разработанные в настоящее время методики расчета торцевых уплотнений валов в большинстве случаев описывают контактную пару, одним из элементов которой является специальное профилированное кольцо. Его начальное поджатие к уплотняющей поверхности обеспечивается упругим элементом (пружиной или сильфоном), который может быть, как подвижным, так и неподвижным. В работе [1] приводятся основные типы таких уплотнений, представленные на рис. 1. Расчет осевого усилия, передаваемого такими уплотнениями на контактную поверхность, не представляет большой сложности. Его слагаемыми являются начальная величина силы сжатия упругого элемента и разница сил гидравлического давления, воздействующих на противоположные стороны профилированного кольца.

В торцевом мембранном уплотнении, типичное исполнение которого представлено на рис. 2, осевое усилие поджатия также состоит из двух составляющих, одно из которых реализуется посредством усилия сжатой пружины, воздействующей на центральную втулку.

Более существенным по величине является второй компонент суммарного усилия, возникающий вследствие воздействия избыточного гидравлического давления на кольцевую площадь упругой тонкостенной мембраны. Очевидно, что из-за перераспределения нагрузок только часть данного усилия приходит на центральную втул-

ку, создавая в итоге вместе с пружиной контактное давление торцевого уплотнения. Остальная составляющая гидравлического давления приходит на периферийный участок мембраны по месту ее окружной заделки и не участвуют в создании контактного давления. Нахождение теоретической зависимости, определяющей усилие в уплотнительном элементе в зависимости от геометрических пропорций мембранного узла, в дальнейшем позволит выполнять различные виды расчетов данных уплотнений, в том числе по моментным характеристикам трения.

Цель исследования . Для различных соотношений характерных диаметров d (посадочный диаметр центральной втулки) и D (периферийный диаметр мембраны) необходимо найти относительную величину нагрузки, передаваемую мембраной на центральную втулку.

ПОСТАНОВКА ЗАДАЧИ, МЕТОДИКА ПРОВЕДЕНИЯ РАСЧЕТА

Принимаем, что результирующее усилие F от равномерно распределенного по кольцу гидрав- лического давления p сосредотачивается в виде погонной кольцевой нагрузки, прикладываемой по диаметру Dц, проходящему через центры масс каждого элементарного кольцевого секто- ра с углом при вершине δα. Положение центра масс для сектора определяется по формуле:

2Rn sin a R^= —

4 3a где RD– радиус, соответствующий диаметру D, мм. С учетом уравнения sin a lim---- a^O a

= 1

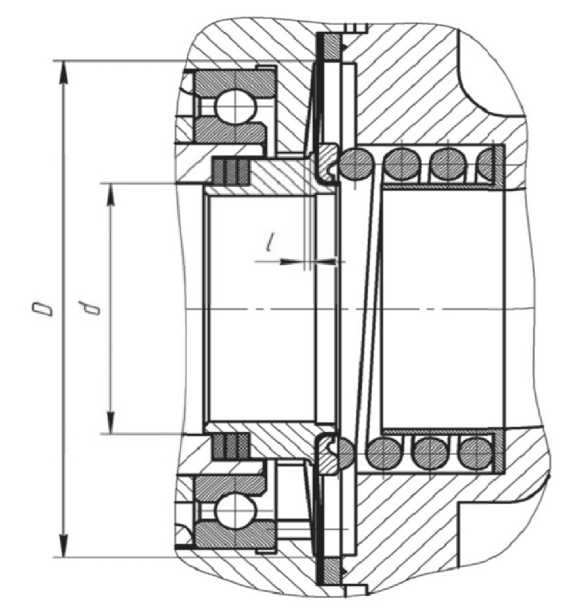
Рис. 2. Торцевое мембранное уплотнение

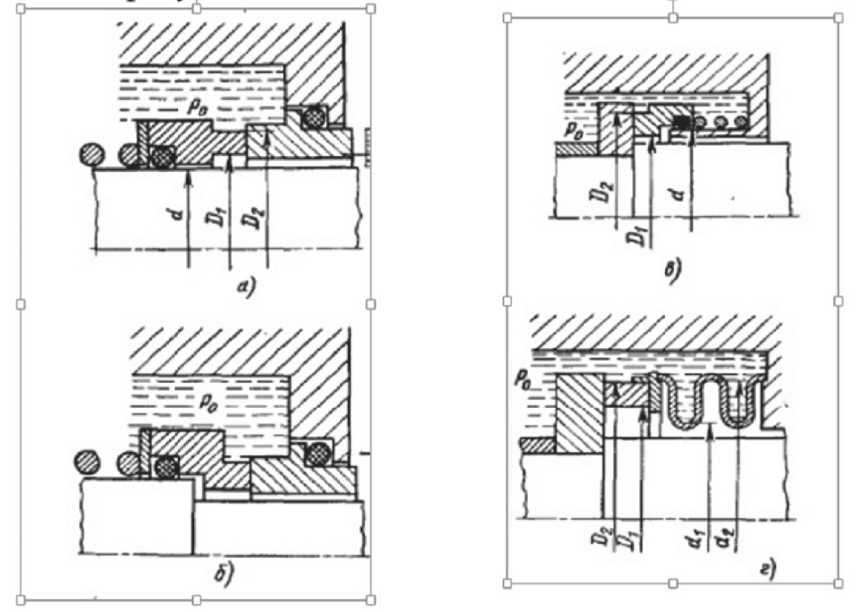
Рис. 1. Схема торцевых уплотнений с подвижными (а, б) и неподвижными (в, г) упругими элементами

для малых углов 5а положение центров масс элементарных секторов принимает окончательный вид:

Л ц =|л₀.

Вычислим положение центра масс участка кольца (кольцевого сектора), приведенного на рис. 3.

Площадь сектора, ограниченного углом 5а и радиусом R D , вычисляется по формуле:

S = uR^q — = uR q ■ к.

2л

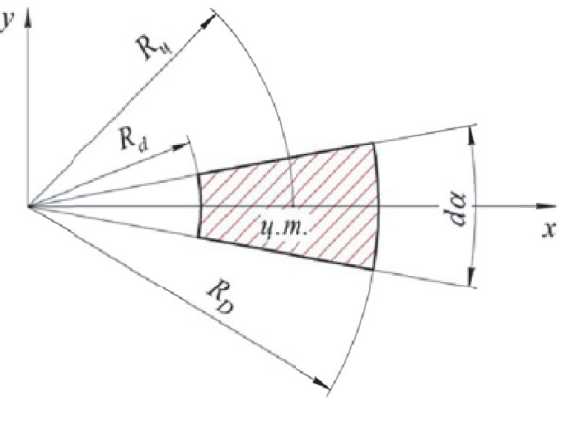
Рис. 3. Определение центра масс кольцевого участка

Площадь сектора, ограниченного углом 5а и радиусом R d :

S 1 = pR^Q |^ = uR^q ■ к.

2л

Площадь участка кольца:

SK = S — S1.

Соотношение между отдельными площадями и координатами их центров масс устанавливается уравнением:

S ■ х = SK ■ Rц + S1x1, где x - координата центра тяжести сектора, ограниченного RD, мм;

х 1 - координата центра тяжести сектора, ограниченного R d ,мм;

R _ц - координата центра тяжести участка кольца, мм.

Тогда координата центра тяжести элемен- тарного кольцевого сектора, ограниченного ра диусами RD, Rd и углом 5а составит:

НЦ

S - х — S±x± S-S±

)

НЦ

кНО-к-^Ко — nR2d-k-^Rd (kRO — кН^) " к

2/R g^— R |\

^{Н ц} з^ — r²J-

/

Суммированием погонной кольцевой нагрузки по диаметру Dц данного элементарного кольцевого сектора получаем результирующее усилие 5F, которое также приложено по диаметру Dц (Dц=2Rц). Ввиду эластичности мембраны пренебрегаем изгибающим моментом по ме- стам заделки.

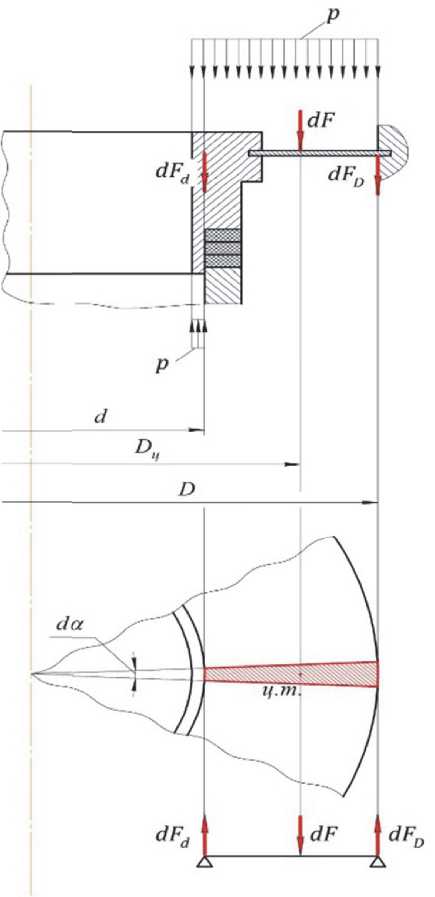
Рис. 4. Распределение нагрузок в мембране

Рассматривая каждый элементарный сектор как элементарную двухопорную балку, принимаем, что усилие 5 F распределяется на втулку и на периферийную заделку обратно пропорционально расстоянию от точки приложения усилия 5 F до наружного и внутреннего диаметра (до наружной и внутренней опоры) (см. рис. 4).

Исходя из имеющихся геометрических соотношений:

'    8f(₀ ^{- 2}з^—^

_о п- ² ^³ — ^

SFd = D 3\D2 — d2)§F        (D — d)    "

После преобразований получаем:

§ F_d _    D³ — 3d²D + 2d³

"gF “ 3(D³ — Dd(D + d) + d³)"

Очевидно, что для всей кольцевой площади мембраны выполняется такое же соотношение между суммарной нагрузкой и ее частью, приходящейся на центральную втулку:

5 F_d _    D³ — 3d²D + 2d³

“SF “ 3(D³ — Dd(D + d) + d³)"

Особенностью конструкции торцевого мембранного уплотнения является наличие конического бурта, расположенного за мембраной. Под воздействием давления мембрана прогибается и касается конического бурта по окружности D 1 (см. рис. 5).

В таком случае диаметр D 1 следует рассматривать вместо периферийного диаметра D , и

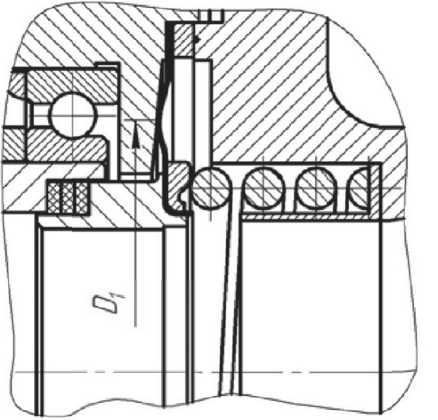
Рис. 5. Рабочее положение мембраны

Таблица 1. Значения параметра F _d / F при различных отношениях D ₁ и d

	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9
F	0,363	0,389	0,410	0,429	0,444	0,458	0,471	0,481	0,491

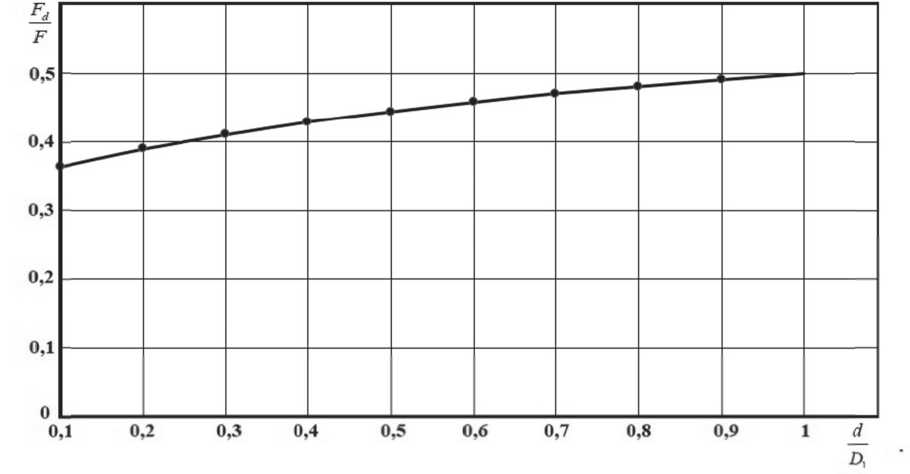
Рис. 6. Относительная величина нагрузки на центральную втулку при различных соотношениях D ₁ и d

соотношение (4) принимает окончательный вид:

F_d _    D f - 3d²D_T + 2d³

"F" ” 3(Df - DTd(DT + d) + d3)

В табл. 1 представлены данные по соотношению F _d / F при различных сочетаниях диаметров D ₁ и d . Соответствующий график зависимости относительной величины нагрузки, приходящейся на центральную втулку, от геометрических характеристик мембраны представлен на рис. 6.

Указанный график носит теоретический характер. Значения функции лежат в диапазоне 0,33…0,50. Очевидно, что при крайних значениях аргумента функции реальное исполнение мембраны невозможно. Так, при d/D1 = 0 в мембране отсутствует центральное отверстие (втулка) для протока рабочей среды. При d/D1 = 1,0 рабочий участок мембраны вырождается в окружность, что исключает восприятие ею какого-либо гидравлического нагружения. Однако, внутри приведенного диапазона аргумента (0…1,0) реальное конструктивное исполнение мембранного узла вполне осуществимо, что делает полученный график пригодным для прове- дения теоретических расчетов усилий, возникающих в торцевых уплотнениях.

ЗАКЛЮЧЕНИЕ

Получена теоретическая зависимость, показывающая перераспределение нагрузок в мембранном узле между центральной втулкой и периферийным кольцевым местом заделки (или промежуточной опорой). Найденная зависимость описывает любое реальное исполнение мембранного узла в виде тонкостенного кольца с центральной втулкой, в котором имеется геометрическое разнесение диаметров втулки и кольцевой линии соприкосновения мембраны с опорой. Полученные значения функции необходимо использовать при расчетах в качестве коэффициента, показывающего долю от общего гидравлического усилия, которая непосредственно формирует контактное давление в торцевом мембранном уплотнении.