Определение жесткости костной ткани при поступательных перемещениях и поворотах корня зуба

В практике ортодонтической стоматологии зачастую возникают проблемы, связанные с прогнозированием перемещений и поворотов зубов при необходимости устранения различных дефектов и аномалий. В связи с этим представляется актуальной разработка соответствующей модели корня зуба в нормальной и ослабленной костной ткани. Поскольку в системе корень зуба – периодонт – костная ткань периодонт не может обеспечить необходимые перемещения и повороты для устранения аномалии зубного ряда, при построении модели целесообразно отдельно учитывать упругость периодонта и упругие характеристики костной ткани. Также следует учесть, что при устранении дефектов зубных рядов основную роль берет на себя костная ткань. Поэтому можно предположить, что общее перемещение зуба можно представить в виде суммы перемещения, обусловленного упругими свойствами периодонта, и перемещения, определенного упругостью костной ткани. Расчеты перемещений корней зубов в периодонте выполнены в монографии [2]. В настоящей работе развивается это актуальное направление, связанное с разработкой модели перемещения корня зуба как абсолютно твердого тела в костной ткани, и выполнен расчет жесткости при поступательных перемещениях и малых поворотах корня зуба с учетом атрофии костной ткани. Под атрофией в данном случае подразумевается вертикальная резорбция (рассасывание) костной ткани альвеолы [2, 4]. Необходимость учета атрофии костной ткани обусловлена тем обстоятельством, что при горизонтальной и вертикальной резорбции выносливость зуба существенно снижается и исчерпывается способность выдерживать нагрузки, развиваемые ортодонтическими аппаратами [2, 4]. Следует отметить, что вопрос определения жесткости упругих биомеханических систем традиционно является актуальным. В частности, в монографии [4]

Юркевич Кирилл Сергеевич, аспирант кафедры теоретической и прикладной механики, Минск сформулированы определения жесткости и податливости упругих систем и биоконструкций. Тем не менее расчеты жесткости костной ткани в работе [4] не выполнены.

Уравнения равновесия корня

Будем считать корень зуба абсолютно твердым телом, геометрическая форма которого описывается уравнением эллиптического двуполостного гиперболоида

F ( x 1 , x 2 ,

x 3 ) = x ₃

^^^^^^^^

H

A

^^^^^^^B

xx

- л Л + , + p p p ( V ak b

- p = 0,

7

где H – высота корня зуба; p – параметр, характеризующий закругление вершины корня зуба; a_k = a 1 при x <  0 и a_k = a 2 при x >  0, a 1 , a 2 , b - полуоси эллипса в сечении корня зуба плоскостью, проходящей по поверхности десны ( x ₃ = H ). Геометрические размеры корня зуба обозначены на рис. 1.

Упругие перемещения u ₁ , u ₂ и u ₃ костной ткани, примыкающей к корню зуба, представим в виде, позволяющем учесть неограниченное уменьшение перемещений при удалении от поверхности корня зуба:

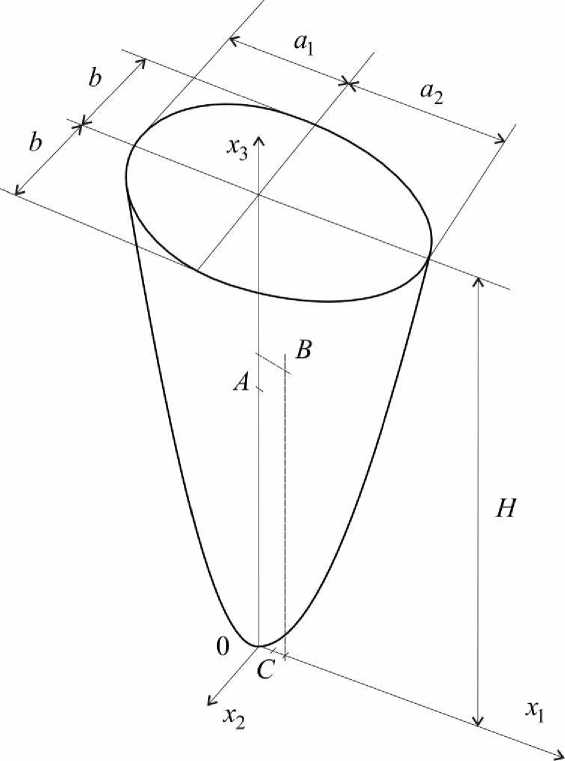
Рис. 1. Центры сопротивления корня зуба

U₁ =

H ( u 1 ) + Ф 2 ( x 3 — x 3 ’ ) — Ф 3 x 2 )

H — F ( x₁, x 2 , x₃ )

,

uL(0)+m — r(BЦ —     — r(B)И u2

"^H I U2 + т3 I xi   xi   ) t1 I x3   x3   J I

H — F ( x ₁, x ₂, x ₃ )

u

H ( u 3 ^ + Ф 1 x 2 — Ф 2 ( x i — x i

³           H — F ( x ₁, x ₂, x ₃ )

Здесь u k "' - поступательные перемещения корня вдоль осей координат; ф _к - углы поворота корня зуба относительно осей координат, к = 1,3 ; x i B ) , x i C ) , x 3 A ) и x 3 B ) -координаты центров сопротивления корня. На поверхности корня зуба F ( x ₁, x ₂, x ₃ ) = 0

перемещения u1 , u2 и u3 совпадают с перемещениями абсолютно твердого тела. Отметим, что центрами сопротивления являются точки A (0,0, x3A)), B (xiB), 0, x3B)) и C(x1 C) ,0,0), через которые проходят линии действия двух горизонтальных и одной вертикальной сил, под действием которых зуб получает только поступательные перемещения. Линия действия силы, проходящая через точку A , параллельна координатной оси x1 , проходящая через точку B , – параллельна оси x2 и проходящая через точку C , – параллельна оси x3 . Центры сопротивления и полуоси эллипсов схематично обозначены на рис. 1.

Выпишем условия равновесия (равенство нулю главного вектора и главного момента сил, действующих на зуб, а также напряжений, возникающих на поверхности F ( x i , x 2 , x 3 ) = 0) [1]:

jj (n-о) dF — P> = 0, jj Г x( П-o) dF — fm = 0, (3)

FF где m = (m1, m2, m3) — главный момент внешних сил; J1 = (P1, P2, P3) — главный вектор внешних сил; г — радиус-вектор, проведенный из соответствующего центра сопротивления; n = ( n1, n2, n3) — единичный вектор нормали к поверхности F (x1, x2, x3 ) = 0; о — тензор напряжений. Для изотропной среды компоненты тензора напряжений имеют вид [1]

(           2v5.. Л    ^ E о,= G diuj+djui+ — £dkuk , G = ( а ,               (4)

V              1—v к=1     у       2(i+v)

где G — модуль сдвига костной ткани, E — модуль упругости костной ткани, v — коэффициент Пуассона костной ткани, 8 j = 1, если i = j , 8 j = 0, если i ^ j , д i = д/д x i i , j = 1,3. Компоненты единичного вектора нормали определяются следующим образом:

n

k

d k F A

E (d F )² , k = 1,3.

i = 1

Жесткости при поступательных перемещениях

Подставим компоненты единичного вектора нормали (5) и тензора напряжений (4) в условия равновесия (3) и выделим коэффициенты при поступательных перемещениях u ^ и углах поворота ф _k , k = 1,3 . После несложных преобразований получим следующую систему уравнений равновесия относительно трех компонент вектора поступательных перемещений и трех компонент вектора углов поворота:

5 123 ⁺ x 3 ’ ^C 12 ) ^ф 1 ⁺

( 0 )„        ( 0 )            ( 0 )

^u 1 c l + u 2 ^C 12 + u 3 ^С 13 + 1 5 132

^+ф 2 ( ⁵ 13

( A )       ,

- x 3 ц + 5 311

C x ₁ ^{( )} c ₁₃

) ^{+ ф} 3 ( ^x 1 cC 2₂

s 211

⁵ 12 ) = ^P1 ,

u 1 ^{( 0 )} c ₁₂ + u 20 ) C 2 + u 30 ) c ₂₃ + Ф 1 ( x 3 B ) c 2

⁵ 23

⁵ 322 ) ⁺

⁺ ( ⁵ 321    ⁵ 123

_

^X 1 ^ ^C 23 ⁺ x 3 ^ ^C 12 ) ^ф 2 ^{+ ф} 3 ( ⁵ 122 ^{+ 5} 21

- X 1 ⁽ B ) C 2 ) = P 2 ,

^U 1 ^ ^C 13 ⁺ u 2 ^ ^C 23 ⁺ u 3 ^ ^C 3 ^{+ ф} 1 ( ⁵ 32

-

x 3 C 23 ⁺ 5 233 ) ⁺

^+ф 2 ( x 3 ^ ^C 13

-

( C )„ 5 ₁₃₃ + x ₁ C ₃

-

⁵ 31 ) ⁺ ( ⁵ 132

-

⁵ 231 ^{+ x} 1 ^ ^C 23 ) ^ф 3    ^P3^.

Здесь введены следующие обозначения:

C< = GH fi ^dF , 4 A

F

g i = — E( YS /k ⁺ 1 ) ^d k F ^-d F , m k = 1

C j = c„ = GH ( y- 1 ) jj

F

1 d F d F dF m d x i d X j A

, 5 , = GH jj X j g i dF , F ^A

5al = GH(Y-1)ffxkdF dFdF, 5   GH(Y- 1)1Ji aF SFdF, m dx. dx. A                     m оx. dx. A

F i j                    F ji

m

= ( H - F ( x 1 , x 2 , x 3 ) ) 2 , Y =

2 ( 1 -v )

1 - 2 v

i ^ j ^ k = 1,3.

Интегрирование соотношений (6) выполним с учетом атрофии костной ткани в обобщенной цилиндрической системе координат:

H I ^r + p - p )

x 1 = a_kr cos ( 0 ) , x ₂ = br sin ( 6 ) и x ₃ =----,      -------,

V1 + p2 - p где ak = a1 при п/2 < 0 < 3л/2, ak = a2 при -л/2 < 0 < л/2, 0 - полярный угол, r - безразмерный радиус. Выражения для полуосей эллипса ak и b на поверхности корня зуба, а также высоту H корня, находящегося в костной ткани, при атрофии представим в следующем виде:

ak

a 0 к

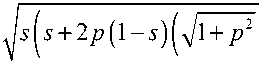
- p ) ) , к = 1, 2,

b = b o ^s ( s + 2 p ( 1 - s ) (7 1 + p ² - p ) ) , H = H о s ,

где a0k, b0 - полуоси эллипса, ограничивающего профиль сечения корня зуба в норме, H0 - высота корня зуба в норме, s - параметр, характеризующий высоту костной ткани, связанной с периодонтом (0 < s < 1). После несложных преобразований будем иметь u1 cci + ф2 (s13

^- x 3 A ) С 1 + s ₃₁₁ ^- x C ) с ₁₃ ) = P ,

U 20 ) С 2 + ф 1 ( x 3 B ) С ₂

-

s 23

-

s 322

) + Фз (

s 122

+ s ₂₁

-

x ⁽ B ) С 2 ) = P 2 ,

u 3 ^С 3 ^{+ ф} 2 ( x 3 ’ ^С 13

s 133

+ x 1 ⁽ C ) С 3

^s 31 ) = ^P3^.

Поскольку сила, приложенная в центре сопротивления в соответствующем направлении, вызывает только поступательное перемещение зуба, коэффициенты при углах поворотов ф _к , к = 1,3 в уравнениях (9) приравниваем к нулю. В результате будем иметь систему четырех уравнений для нахождения координат центров сопротивления x 3 A ) , .v , B ) и x 3 B ) , x 1 ⁽ C ) . Решая систему, находим

x 3 A ) =

^С 13 ^{( s} 133 ^{+ s} 31 )    ^С 3 ^{( s} 311 ^{+ s} 13 )

^С 1 ² 3 ^{- С} 1 ^С 3

( B ) _ ^s 122 ⁺ s 21     ( B ) _ s 322 ^{+ s} 23

x 1                    , X 3

c ₂                  c ₂

x j C ) =

^С 13 ^{( s} 311 ^{+ s} 13 )   ^С 1 ^{( s} 133 ^{+ s} 31 )

c ₁₃    c ₁ c ₃

Отсюда после интегрирования соответствующих коэффициентов (7) по поверхности (1) получим следующие выражения для координат центров сопротивления:

( B ) 8 a 1 a ₂ ( a 1 - a ₂ ) ( 3 b²r 1 + у H ² ( 1 - 3 p ² + 3 p ³ arctan (1/ p ) ) )

¹      9 n ( b²H² + a 1 a ₂ ( y H ² + 2 b²r 1 ) - H²p²r₂ ( b² +y a 1 a ₂ ) ) ,

x j C ) =

8 a 1 a ₂ ( a 1 - a ₂ ) ( 3 y b ² r 1 + H² ( 1 - 3 p ² + 3 p ³ arctan ( 1 p ) ) ) 9 n ( b ² H ² + a 1 a ₂ ( H ² + 2 y b ² r 1 ) - H ² p ² r ₂ ( b ² + a 1 a ₂ ) )

x 3 A ) = H ( H ² ( 2 - 3 p ² - 12 p ⁴ )( a 1 a ₂ + у b ² ) + 2 a 1 a ₂ b ² ( 1 + y+ p ² ( 2 - y ) ) +

+ p4 1 + p ² ( a1 a ₂ ( 3 H ² ( 1 - 4 p ²) - 2 b ² ( 2 - y ) ) + 3 y b²H ² ( 1 - 4 p ²)) + + 3 H²p³r ₂ ( p ( 3 + 4 p ²) + ( 1 + 4 p ²) 4 1 + p ²) ( a 1 a ₂ + Y b ² ) )/ 3 ( a 1 a ₂ ( 2 b ² + H ² r 1 ) + H ² r 1 r ₂ ( y b ² + p ² ( a 1 a ₂ + y b ² ) ) )

x 3 B ) = H ( H ² ( 2 - 3 p ² - 12 p ⁴ )( у a 1 a ₂ + b ² ) + 2 a 1 a ₂ b ² ( 1 + y+ p ² ( 2 - y ) ) + + p V 1 + p^г ( a 1 a ₂ ( 3 Y H ² ( 1 - 4 p ²) - 2 b ² ( 2 - y ) ) + 3 b²H^г ( 1 - 4 p^г ) ) +

+ 3 H²p³r ₂ ( p ( 3 + 4 p ² ) + ( 1 + 4 p ²) V1 + p² ) ( y a₁ ( 3 ( a ₁ a ₂ ( 2 b ² + y H ² Г ) + H ² r ₁ r ₂ ( b ² + p ² ( y a 1 a ₂

где f = ( 4 1 + p² - p ) , r 2 = ln (V p ² + 1 ) .

Система (9), в случае если силы прикладываются в центрах сопротивления вдоль соответствующих осей координат, принимает вид uk°’ck = Pk, k = 1,3.

Здесь коэффициент ck является жесткостью костной ткани при поступательном перемещении зуба вдоль координатной оси 0xk и численно равен силе, вызывающей перемещение корня, равное 1 м. Для нахождения жесткостей ck выполним интегрирование соответствующих выражений (7). В результате будем иметь c =

( a 1 + a ₂ ) G n ( 2 a 1 a ₂ b ² r 1 + H ² ( a 1 a ₂ +Y b ² ) - H ² p ² r ₂ ( a 1 a ₂ +Y b ² ) )

4 bHa ₁ a ₂ r ₁

( a 1 + a ₂ ) G n ( 2 a 1 a ₂ b ² r 1 + H ² ( y a 1 a ₂ + b ² ) - H ² p ² r ₂ ( y a 1 a ₂ + b ² ) )

c ₂ =------------------------------------------------------------------- ,          (14)

4 a ₁ a ₂ bHr ₁

__/ /          . i 2 \ т t2 .            7 2..        т t2 2    /             7 2

c 3

a 1 + a ₂ ) G n l ( a 1 a ₂ + b ) H + 2 a 1 a ₂ b Yf ₁ - H p r 2 ( a 1 a ₂ + b

4 a ₁ a ₂ bHr ₁

Заметим, что при 5 = 1 выражения (14) определяют жесткости в норме, при 5 = 0 жесткости равны нулю. Для промежуточных значений параметра s жесткости изменяются в соответствии с уравнением поверхности корня зуба (1).

Проведем расчет жесткостей на примере клыка ( a ₁₀ = 2, a ₂₀ = 5, b ₀ = 4, H ₀ = 15,7 мм, p = 0,5) и премоляра ( a ₁₀ = a ₂₀ = 5, b = 3,5, H ₀ = 14,3 мм, p = 0,4) [3]. Упругие свойства костной ткани характеризуются константами E = 16,1 ГПа, v = 0,25 [5]. На рис. 2. представлены зависимости жесткостей при поступательных перемещениях корней этих зубов от параметра s , характеризующего атрофию костной ткани.

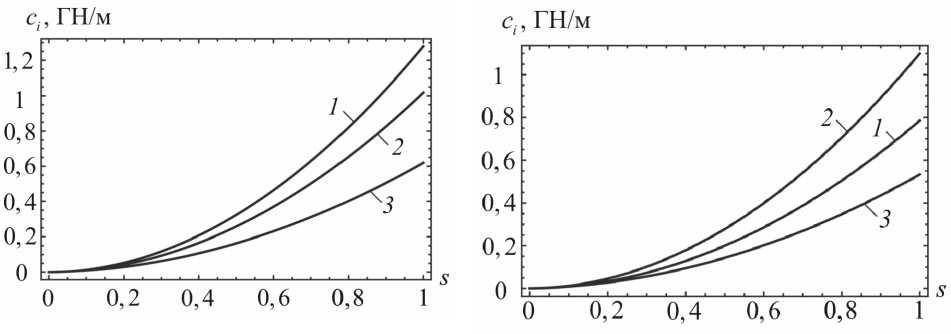
а

б

Рис. 2. Зависимости жесткостей костной ткани при поступательных перемещениях корней клыка ( а ) и премоляра ( б ) от параметра s , характеризующего атрофию костной ткани:

¹ - ^c 1 ; ² - ^c 2 ; ³ - ^c 3

В зависимости от величин полуосей a_k и b выполняются различные соотношения между жесткостями. В случае если а 1 + а ₂ >  2 b , имеем c ₂ >  c 1 , что наблюдается для жесткостей костной ткани при поступательных перемещениях премоляра. При 2 b >  а 1 + а ₂ получаем c₁ >  c ₂ (результаты вычислений для клыка). Жесткости c ₁ и c ₂ превышают жесткость c ₃ независимо от значений полуосей эллипса.

Жесткости при поворотах

Для нахождения жесткостей костной ткани ц i и ц ij , i ^ j = 1,3 при поворотах корня зуба выделим коэффициенты при углах поворота ф i в уравнениях второй группы уравнений равновесия:

c ф1и1 + s ф12 u 2 + s ф13 u 3 + Ц1ф1 + Ц12ф2 +Ц13ф3 = ml, s ф21и1 + c ф2 u 2 + s ф23 u 3 +Ц12ф1 +Ц2ф2 + Ц23ф3 = m 2, sф31и1 + sф32u2 + cф3u3 +Ц13ф1 + Ц23ф2 +Ц3ф3 = m3.

Коэффициенты системы (15) определяются следующим образом:

(B)                               (C)( cф1 = s123   s132   x3  c12 , cф2 = s231   x1  c23   s123 + x3

(B)( cф3 = x1 c23 + s132 s231, sф12 = x3 c2 s23 s322 , sф13 = s32 + s233 - x3 c23, sф23 = X1 c3 - s31 + x3 c13 - s133 ,

_          (A) ,            (C)_ ( s ф21 = s13 X3 c1 + s 311 X1 c13 , s ф31 = X1 c12 s 211 s12,

( B )

s ф 32 = s 21 ^X 1 c 2 ⁺ s 122 ,

И 1 = GH jj g 2 ( ^x 3

F к

x 3 ' ) ) + g ₃ x 2 + 2 ( 1 — y ) x ₂ ( x ₃

x 3 ' ) )

1 д F д F ) dF

m д x ₂ д x _{3 7}

А ’

F

x ₃

^x 3 A ) ) ⁺ g 3 ( ^x 1

x C ) ) ²

+

И =

+2 (1— Y)

1 д F д F

m д x 1 д x ₃

( ^x 1

в

^x 1 C ) )( ^x 3

к

в

x

. ( A )\ ] dF

3 )J А ’

G Jj g 2 ( x

0 F

^x 1 ⁽ ' ) ) ⁺ g 1 ^x 22 ^{+ 2} ( 1 ^— Y ) ^x 2 ( ^x 1

x^' ) )

1 д F д F ) dF

m д x 1 д x _{2 7}

А ’

Ц12 = Ц 21 =

gh\f1 x ( m

F

(1 — у) (x.

x ₃

+ ( 1 "^ ( ( ^x 3 к

x ₁

B

x ₁

x 1 C ) )

и

д F

д F

к2 ^

^ц 13    Ц 31

кк дx 2 J

+ Y 4-дx3 J

к

J

( ^x 3

B

x

.( ' )

+ ( x3

B

Здесь величины

x 3 ' ) )

д F д F

д x ₂ д x ₃

+ Y ( x1

x C ) )

x ₂

д F

к

^{д x} 1 J

+

x 1 ^{( C )} ) ( x 3

B

д F

) д x ₂^{2 (} ~

_x ( ' n^ F x ₃

G^HS I¹ ( ^JF m ^v

к

(Л \ д F ⁺ ( 1 ^— Y ) ^x 2X— ^{д x} 3 к

) ( X 1 x ! ' ’ )

д F

B

_x ( a ) )— ³ ' д x

dF

А ’

x ₁

^x 1 ' ) )( ^x 3

( X 1 ^

. ( ' ) )d F ' д x ₂

x

_:3 ' , I F

’ к дx3 J

B

x

д F

к

д F

к

^{д x} 1 j

+

к

^ц 23

B

+

кк дx1 J

+ Y

к дx2 J

Ц 32 = ^— GH^ f— * 2 ( m

(1— Y)( X1

^x 3 A ) )

x ₂

к

ц i и ц..

зуба, причем жесткость

F

к

д F

к дx2 J

x ₃

+ (1 Y) X2

д F д F

dF

J

B

x

д x 1 д x ₂

_:3 A > ) I F

7 к дx3 J

B

А ’

к

) aF [(* — X' k^F )дx3 к( 1 1 )дx 2

. ( C A^ F

+ (1 — Y)( x.

B

x

д F

дx1 7

+

д F д F

д x 1 д x ₂

+

Y x ₂

д F

к

dF

являются жесткостями костной

ц i численно равна моменту

к дx1 J

А

.

ткани при поворотах корня

сил, который необходимо

приложить к зубу, чтобы повернуть его на угол ф i = 1, а жесткости ц ij численно равны

моменту сил, который необходимо приложить к корню зуба относительно оси x_i ,

чтобы повернуть его относительно оси x j на угол ф j = 1.

µ _i , кН ·м                                       µ _i , кН·м

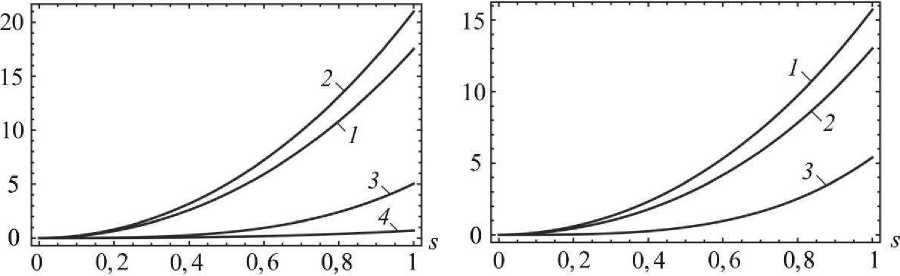
а                                       б

Рис. 3. Зависимости жесткостей костной ткани при поворотах корней клыка ( а ) и премоляра ( б ) от параметра s , характеризующего атрофию костной ткани: 1 - µ ₁ ;

2 - µ ₂ ; 3 - µ ₃ ; 4 - µ ₁₃

Подставляя координаты центров сопротивления (10) - (13) в соотношения (16) - (22) и интегрируя полученные выражения в обобщенных цилиндрических координатах, получаем равенство нулю всех коэффициентов (16), а также выражения для жесткостей костной ткани при поворотах зуба (в силу громоздкости результаты интегрирования не приводятся). На рис. 3 приведены зависимости жесткостей µ _i и µ ₁₃ , i = 1, 3 от параметра s , характеризующего атрофию костной ткани, для клыка и премоляра (жесткости µ ₁₂ и µ ₂₃ равны нулю).

Как следует из рис. 2 и 3, численно жесткости при поворотах существенно меньше жесткостей при поступательных перемещениях. В частности, максимальное значение жесткости костной ткани µ ₂ для клыка составляет ≈ 21 кН ⋅ м. Это указывает на более высокую подвижность зуба при поворотах, чем при поступательных перемещениях даже при незначительных нагрузках в виде моментов сил. При атрофии костной ткани более 50% ( s <  1/2) жесткости при поворотах существенно уменьшаются. При профиле сечения корня зуба с одной осью симметрии все жесткости костной ткани при поворотах различаются между собой (см. рис. 3, а ), тогда как при профиле корня с двумя осями симметрии жесткость µ ₁₃ оказывается равной нулю.

Заключение

Представленный в настоящей работе подход к определению жесткостей периодонта при поступательных перемещениях и поворотах корня зуба позволяет корректно учитывать влияние атрофии костной ткани на их значения. В частности, при полном отсутствии костной ткани соответствующие формулы приводят к нулевым значениям для жесткостей. Выражения для констант c_i , µ _i и µ _ij могут быть непосредственно использованы для расчета перемещений корня зуба и напряжений в костной ткани, возникающих при действии на зуб сосредоточенной силы и момента сил.

Работа выполнена в рамках инновационного проекта «Разработать методику автоматизированного проектирования и оптимизации конструкций зубочелюстных протезов и ортодонтических аппаратов при аномалиях и деформациях челюстнолицевой области, обусловленных расщелинами губы и неба, с применением универсальных CAD/CAE/CAM-систем» Государственного комитета по науке и технологиям Республики Беларусь.