Optimal control of solutions to the initial-final problem for the model of linear waves in a plasma

Let Q = (0, a) x (0, b) x (0, c) c R3. The article investigates the optimal control of solutions to the following problem:

d ² x ( s.t )

(X - A)xtttt (s, t) = (A - X )xtt (s, t) + a-----r-^- + u(s, t), s e Q, t e (0, т), tt                ds2

x ( s , t ) = 0,  ( s , t ) g dQ x (0, t ).

Model (1), (2) describes ion-acoustic waves in plasma in an external magnetic field [1]. The parameters in equation (1) relate such physical quantities as the ionic hydro frequency, the Langmuir frequency, and the Debye radius. The function x(s, t) represents the generalized potential of an electric field, the function u(s, t) represents an external effect.

Problem (1), (2) is investigated in the framework of the theory of relatively polynomially bounded pencils of operators [2]. Consider a high-order abstract Sobolev type equation

Ax ⁽ n ) = B_n - i x ⁽ n ^-1) + • • • + B ₀ x + y + Cu ,                              (3)

where the operators    A , B n _ ₁,..., B ₀ e L ( X ; Y ), C e L ( U ; Y ),  the functions u :[0, t ) c R + ^ U ,

y : [0, т ) c R ₊ ^ Y ( т <  да ), X , Y , U are Hilbert spaces.

Supplement equation (3) with initial-final conditions [3]

Pin (x(k)(0) -xk) = 0, Pfin ( x(k)T) - xT) = 0, к = 0, n -1,

where Pin(fin) are some projectors in space X. Thus, the optimal control problem is to find a pair (.x,й), where xˆ is a solution of (1), (2), and uˆ ∈Uad is the control for which the relation J(jx, ui) = min(x,u)exxvad J(x,u)

holds.

Here J ( x , u ) is some specially constructed penalty functional, and U_ad is a closed convex set in the space of controls U .

Many non-classical models of mathematical physics [4–9] are based on Sobolev type equations. For example, they occur in problems of hydromechanics, plasma physics, atmospheric physics, filtration theory, theory of electrical circuits, and others. In the work, to find the optimal control of solutions to linear Sobolev type equations of high-order, the ideas and methods obtained by G.A. Sviridyuk [10] and his students [11–13] in the study of first-order Sobolev type equations are used. Here the initial-final problem [14] is investigated. A distinctive feature of this problem is that one projection of the solution is specified at the initial moment of time, and the other at the final point. The initial-final problem for the first-order Sobolev type equations was considered by G.A. Sviridyuk and S.A. Zagrebina.

1.    Polynomially A-bounded operator pencils and projectors. Strong solutions

By B denote the pencil formed by operators B n _-1,..., B₀. The sets p^A ( B ) = { p G C :(pⁿA - -p^{n -1} B_{n - 1} -...- pB₁ - B ₀ )^-1 g L(Y ; X )} and ст^A ( B ) = С \ p^A ( B ) are called an A - resolvent set and an A - spectrum      of      pencil        B ,       respectively.      The      operator      function

R p A ( B ) = {pⁿA - p ^-1 B n _{- 1} -...- pB₁ - B ₀ )^-1 of a complex variable with domain p^A ( B ) is called an A - resolvent of pencil B .

Let the pencil be B polynomially A -bounded. Introduce an additional condition [15] p k R A ( B ) dp = 0,   k = 0, n - 2,                              (6)

γµ where γ is a contour that bounds the domain containing the relative spectrum of the pencil B . Then the operators

P = -^ f R A ( B)p^{n -1} Adp,  Q =    f p n ^-1 AR A ( B ) dp

2niY p                 2niY      p are projectors in spaces X and Y . Denote X0 = ker P, Y0 = ker Q, X1 = imP and Y1 = imQ . If the pencil of operators is polynomially A -bounded, ^ is a pole of order p g {0} U N of the A -resolvent of pencil B, then the pencil of operators B is called (A, p) -bounded.

Let the pencil B be polynomially A -bounded, (6) hold and the following conditions be satisfied:

c^A ( B ) = c 0 ( B ) и C A ( B ), c kA ( B ) * 0 , k = 0,1;

and there is a circuit y c C, 0      ,(7)

bounding the domain Г ₀ c C such, that

Г 0 П C A ( B ) = C A ( B ), Г 0 n C ( B ) = 0 .

f pmRA (B)dp = 0, m = 0, n - 2.(8)

J Y0

Operators

P fin =-L J pR p A ( B ) Ad pg L ( X )

2 ni ^J

Y 0

and P in = P - P fin g L ( X ) are projectors in space X [15].

Definition 1. The vector-function x g Hⁿ ( X )={ x g L ₂(0, t ; X ): x ^{( n} ) g L ₂(0, t ; X )} is called a strong solution of linear non homogeneous Sobolev type equation

Ax ^{( n} ) = B_{n - 1} x ^{( n -1)} +... + B ₀ x + y , (9) if it turns the equation to an identity almost everywhere on interval (0, t ) . A strong solution x = x(t ) of (9) is called a strong solution to (4), (9), if (4) holds.

Theorem 1. If the pencil B is ( A , p ) -bounded, p g {0}U N , conditions (6)-(8) are satisfied, then for arbitrary x 0 , x T g X , k = 0, n - 1 and y g H^{p + n} ( Y ) there exists a unique strong solution to (4) for equation (9).

Математика

2.    Optimal control for the model of linear waves in plazma

Consider problem (4) for equation (3), where the functions x, y, u lie in X, Y and U , respectively.

Introduce the control space _o p + n                                                                      ____

H   (U) = {u e L2 (0, t; U): u(p+n) e L2 (0, t; U), u(q) (0) = 0, q = 0, p}, p e {0} U N. It is a Hilbert space with inner product p+n

[ v , w ] = ^JJ ( v ^{( q} ) , w ^{( q} )} ddt .

q =0 о p ⁺ n

In the space H   (U) single out a closed convex subset Uad. A vector function u e Uad is called an optimal control of solutions to (3), (4), if (5) holds.

Let us prove the existence of optimal control u e U_ad , minimizing penalty functional

J ( x , u ) = р ££ ^Т || x ^{( q} ) - x ^{( q} ) ||² dt + v^'£ ^Т( N_qu ^{( q} ) , u ^{( q} )) dt .               (10)

q =0 ⁰                        q =0 ⁰                U

Here p,v >0, ц + v = 1, N_q e L ( U ) , q = 0, 1, ..., p + n , are self-adjoint positively defined operators, and x ( t ) is the target state of the system.

Theorem 2. If the pencil B is polynomially A -bounded, conditions (6)–(8) are satisfied, then for arbitrary x 0 , x j e X , k = 0, n - 1 and y e H^{p + n} ( Y ) there exists a unique optimal control of solutions to problem (3), (4).

Reducing problem (1), (2) to equation (3) put

X = {x e W2+2 (Q): x(5) = 0,5 e SQ},  Y = W^ (Q), d 2 where W2(Q)  are Sobolev spaces. Define the operators A = Я-A, B2 = A-Я, B0 = a—- , dx3

B ₃ = B 1 = O . Operators A , B ₃, B ₂, B 1 , B ₀ e L ( X ; Y ) for all l e {0}U N .

I      ^{n i5}\      ^П j⁵0      ^{n k}S^ |.

Denote by ф_11к = < sin— 1 sin---² sin---³ >  the eigenfunctions of the Dirichlet problem for the

^J ^ a       b        c

Laplace operator, where i , j , k e N , and the corresponding eigenvalues are denoted by

A jk

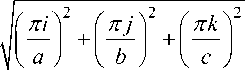
Since {^_ijk } c C ” ( Q ), then we get

Ц A - ^² B ₃

^- Ц ^{2 B} 2

TO

^- P^B 1 ^{- B} 0 = ^

i , j , k =1

^{( Я -} ^ tjk ^{) в} 4 ^{+ ( Я -} ^ ijk )M 2

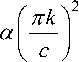
< V ijk , * >  V ijk ,

where <  * , * > is an inner product in L ²( Q ) .

Lemma 1. [15] Let one of the following conditions be satisfied:

• (i)    Я e ^ ( A );

• (ii)    ( Я б о ( А )) л ( Я ^ Я ').

Then the pencil B is polynomially ( A ,0) -bounded, and conditions (6) are fulfilled.

The A -spectrum of the pencil B consists of solutions p | _k , l = 1,4 of equation

^{( Я} ijk ^{- Я )} Ц ^{4 + ( Я} yk ^{- Я} '^{) в} 2 ^{- a} I “ i = °.

Construct the projector

I , if (i) holds ,

P = 1 1 -

Z ^Фук ^Vyk ^{,if (ii) holds} - j = 2

To construct the projector P fin choose a domain Г ₀ c C , containing, for example, a finite set a₀ A ( B ) of points ^ j of the A - spectrum of the pencil B and such that дГ ₀ П ^ OA ( B) = 0 - As it is easy to see, the domain Г ₀ can be chosen such that дГ ₀ = / ₀ is a contour. Thus, condition (7) is satisfied.

Consider the initial-final problem

Z _ < x G^{0) -} x o V jk > V ijk = ^0, j *^,M ijk ^g ^ ' ^{( B} )

Z       <  x t G⁰ ) ^- x ⁰ V jk >  V ijk = ⁰

^ ijk *^,M ljk ^g^^{a ( B} )

Z     _ <  x tt ⁽ ‘ ^,0) - x ⁰’ V yk >  V ijk = ⁰ ,

^ ijk ^-nu ^g " ^{a ( B} )

Z      _ <  x ttt ⁽ - ^{,0) -} x "^{0 ,}V ijk >  V yk = ^0,

• ^x ijk ^^,p ljk ^g ^ 1 ' ^{( B} )

Z         < x ⁽ ‘ ^{, T ) -} x ^{T ,}V ijk > V ijk = ^0,

• ² ijk *^2,M ljk ^g ^ 0 a ⁽ B )

Z         <  x_t C^{, T} ) - x ^T ,V ijk >  V yk = ^0,

• ² ijk *M jk ^g ^ 0 ^{A ( B} )

Z     _ <  x tt ⁽ ‘ , ^{T ) - x} 2 , V ijk >  V ijk = ⁰

• ² ijk *^2,P ljk ^g ^ 0 a ^{( B} )

Z      _ <  xttt ( - ^{, T} ) ^- x ^{T ,}V ijk >  V ijk = ^0,

• ² ijk *^2,M ijk ^g ^ 0 a ^{( B} )

for equation (1) with boundary conditions (2).

Theorem 3. For any ae R and 2 g R such that the conditions of Lemma 1 are fulfilled, and for any т g R + , x ° , x T g X , k = 0,3, there exists a unique solution to the optimal control problem for equation (1) with conditions (2), (12) that minimizes functional (10).