Optimal Design of a RISE Feedback Controller for a 3-DOF Robot Manipulator Using Particle Swarm Optimization

Published Online July 2014 in MECS

In the past few decades, control of robotic systems has been studied significantly, because of their wide spectrum applications in medicine, aerospace, automotive and other industries. Robot manipulators are of highly nonlinear dynamic systems, which suffer from various uncertainties such as nonlinear friction, payload variation, unknown disturbances, and etc. Several control methods have been presented to attain an accurate tracking control of robot manipulators, such as adaptive control [1,2], sliding mode control [3,4], robust control [5] and neural network techniques [6,7].

Adaptive controllers may cope with the uncertainties in the dynamic model, and present fine tracking performance. However, this technique is restricted to compensate uncertainties which are linear in parameters. Sliding mode control is one of the effective strategies to control uncertain nonlinear systems. Main advantage of this method is strong robustness against system uncertainties, parameter variations and nonlinear disturbances [8]. But this technique, has some drawbacks including creating chattering phenomenon due to the discontinuous nature of control law, and the requirement of knowing an exact knowledge of the system dynamics [9].

It is difficult to obtain an exact mathematical model of robotic systems, due to modeling uncertainties, parameters variations, and etc. In recent years, intelligent control approaches such as neural network (NN)-based control and fuzzy control in robotic systems control, have received considerable attention [10,11,12]. Neural networks are almost able to approximate nonlinear continuous functions. They are therefore powerful tools to compensate for uncertainties, without knowing a complete knowledge of the plant [13]. Lewis et al. proposed a multilayer neural network controller for a robot manipulator which guarantees trajectory tracking performance [14]. However due to the NN functional reconstruction error, this type of controllers only achieve uniformly ultimately bounded (UUB) stability results. In order to eliminate the approximation error of NN-based controllers and achieving asymptotic tracking, Wai presented a sliding-mode neural network controller for rigid link manipulators [15]. In spite of obtaining asymptotic results, existence of a sign function in the robust term results in the destructive chattering phenomenon.

Recently, a new feedback control strategy called robust integral of the sign of the error (RISE) is proposed in [16] which compensates for disturbances or uncertainties of dynamic system, by generating a continuous control signal [17,18]. In [19], Patre et al. utilized this method to develop a tracking controller in presence of additive disturbances and parametric uncertainties. The RISE method is a high gain feedback tool. Motivated by this issue , in [20, 21], a NN-based feed-forward term is combined with the RISE feedback term in order to reduce the gain values of RISE feedback and to yield asymptotic tracking results. Also Shicheng Wang et al. in [22], designed a RISE based NN controller for a spacecraft formation within the leader follower architecture.

Particle swarm optimization (PSO) is a relatively new evolutionary computation technique inspired by the social behavior of birds flocking and fish schooling. It was first introduced by Kennedy and Eberhart in 1995 [23]. In fact, PSO is a population-based search method that can be used to find the optimal solution in a multidimensional search space. Optimization of the gains of a state feedback controller for a flexible manipulator, by PSO algorithm is presented in [24]. Also in [25], using PSO algorithm, an optimal design for a 6-DOF parallel manipulator has presented. Unlike other optimization methods, PSO gains from advantages such as simplicity of implementation and fast convergence.

In this paper, using the new RISE feedback control strategy, an asymptotic tracking is obtained for an uncertain nonlinear 3-DOF rigid link robot system. PSO algorithm is applied to tune gains of the RISE controller by minimizing the root mean squared error of the robot. The obtained results represent satisfactory performance of the controller.

The remainder of this paper is organized as follows. First, in Section 2, nonlinear model of a 3-degree of freedom robot manipulator is presented. Then, the RISE feedback control scheme is introduced in section 3. In section 4, PSO optimization technique is described. Simulation results for the 3-DOF robot manipulator are provided in section 5, and eventually, conclusions are given in section 6.

• II.    Dynamics Of Three Link Robot

The dynamics of a general rigid link manipulator having n -degree of freedom in free space is as follows:

This dynamic equation is obtained by means of the Lagrangian approach. In (1) for the rigid 3-DOF robot manipulator q ( t ), ̇( t ) and ̈( t ) ∈ R³ are the position, velocity and acceleration of the joints, respectively. M ( q ) ∈ R^{3 ×3} is the positive definite inertia matrix whilst C ( q , ̇) ∈ R^{3 ×3} represents the Coriolis/centripetal matrix, and G ( q ) ∈ R³ expresses the gravity vector. ^ d ∈ R³ denotes the vector of disturbances and unmodeled dynamics, and т ∈ R³ denotes the input torque vector applied to the joints. Fig. 1 shows the 3-link robot manipulator.

Mi3

M23

M33

In this system the inertia matrix M ( q ) , the Coriolis/centripetal matrix C ( q , ̇) and the gravity vector G ( q ) are as follows [26]:

[Mil M12

M ( q , ̇)=[ ^21 ^22

Lm31 m32

with

Мц =2( сЦ + d₂ + d.3 )+2 й^Сз +2 <^5^C23 +

M12 =2(d₂ + d₃)+ й^Сз + <^5^C23 +2d₆C₃,

Mi3 =2d3 + <^5C23 + d6C3, and

[ ^21 C₂2

Cis

C23

C33

][ ̇̇ ; ], ̇ 3-1

where Q/,( i = 1,2,3, j = 1,2,3) are defined as follows:

Ga =- ̇2<^4S2 ^-<^5⁵23 ( ̇2+ ̇3)- d-e^s3 ̇3,

Cl 2 =- <^4^2 ( ̇1+ ̇2)-<^5523 ( ̇1+ ̇2+ ̇3)

• - й^Зз ̇3,

C13 =-( <^5^23 + й^Зз )( ̇ 1+ ̇2+ ̇3 ),

С21=( <^4^2 ⁺<^5^23) ̇i- й^Зз ̇3,

C22 =- <^653 ̇3,

C23 =- <^653 ( ̇1+ ̇2+ ̇3),

С31 =        ̇1+ <^653 ( ̇1+ ̇2),

C32 =     ( ̇1+ ̇2) , C33 =0, and

Si =₂ a_Y

c_Ym_Yg +(di C^+^1tt2 ^C12 ) m₂g +(di C-^

+ ^a2^C12 +  ^tt3^C123) m₃g ,

92 =(^1a2 ^C12 ) m₂g +

(^a2 ^C12 +  ^tt3^C123) m₃g ,

9з =( ^tt3 ^C123) m₃g .

where q =[Qi q2 q3 ] т and ̇=[ ̇^ ̇2 ̇3] T contain the joints displacement and velocities, respectively. ТП[ and at are the masses and lengths of the joints. Meanwhile Si , Ci , ^SU , Cij and Cijk ( i = 1,2,3, j = 1,2,3, к = 1,2,3) denote sin( qi ), cos( qi ), sin( qi + qj ), cos( qi + Q/), cos( Qi + Qj + Qk ) , respectively, whilst parameters d[ , i =1,…,6 are defined as follows:

^dl — 2 [Ц^ + ^m2 + m 3 ) “² + ^{Io 1} ],

^2 =l[(1m2 +m3V2 +Io2 ]’ йз =|[(1m3)a3 +Io3 ], d4 — (2^ m^ 2 + mt з) a ^a 2,

^ 5 ^— ^^m 3 ^a 1 ^a 3 ,

^ 6 ^— 2 ^m 3 ^a 2 ^a 3 .                               ⁽³⁾

where I_o / , i — 1,2,3 denotes the moment of inertia of i ^th joint [26].

It is assumed that q(t) and q(t) are measurable and M (q), C( q, q), G(q)   and   r_d( t)   are unknown.

Furthermore the following properties for the dynamic model of the robot are hold:

Property 1: The inertia matrix M(q) is symmetric, positive definite and holds true the following inequality:

m₁ ||уП²<  y^TM(q)y < m(q)Hy|² Vy e R ³     (4)

where m₁ e R is a known positive constant, m( q) e R is a known positive function and 1.1 represents the standard Euclidean norm.

Property 2: If q(t), q(t) e£_m , then C(q, q), G(q) are bounded. Further, if q(t),q( t) e £ _ю, then the first and second partial derivatives of the elements of M(q), C(q, q), G(q) with respect to q(t) exist and are bounded, and the first and second partial derivatives of the elements of C(q, q) with respect to q(t) exist and are bounded as well.

Property 3: The nonlinear disturbance term and its first two time derivatives are bounded i.e., Td(t),t_d(t),T_d(t) e £_ю.

• III.    Rise Feedback Controller

Recently a novel feedback control scheme called robust integral of the sign of the error (RISE) is proposed in [16]. This method compensates for the disturbances or uncertainties of dynamic system using a continuous control signal. Using this technique, an asymptotic tracking is achieved without chattering problem that usually occurs in sliding mode controllers.

It is assumed that the desired trajectory q_d(t) e Rⁿ, is designed such that q_d^(l)(t) e £_M,i — 1,2, ^,5. In order to design a controller for the robot manipulator, with the aim of guaranteeing tracking of a desired time-varying trajectory, q_d(t) e Rⁿ , by the system, in spite of uncertainties and bounded disturbances in the dynamic model, a position tracking error, denoted by 6₁(t) e Rⁿ, is defined as:

61 — qd - q

The filtered tracking errors denoted by 62(t) and r(t) e Rn are also defined as:

62 — 61 + «161

r — 62 + «262

where a1 e Rnxn is a positive constant matrix and a2 e R is a positive constant.

The continuous RISE feedback control law to attain the mentioned control objective is as follows [16]:

r(t) —(k_$ + 1)e₂(t)-(k_$ + 1)6 2 (0)

• + [ [⁽k_s + 1⁾«262⁽ff^{)                (8)}

J 0

+ ^ 1 Syn(6 2 («))]d«

Where k_s and ^₁ e R are positive constant control gains and sgn (.) is the standard sign function.

• IV.    Particle Swarm Optimization Technique

• A. PSO Algorithm

PSO is a population-based optimization method inspired by the observation of social behavior of bird flocking. This method consists of a swarm of particles, where each particle represents a potential solution. In a PSO system, each particle flies through the multidimensional search space to adjust its position according to its own flying experience as well as the flying experience of its neighboring particle. In other word, each particle is considered as a point in search space, in which we try to find an optimal location.

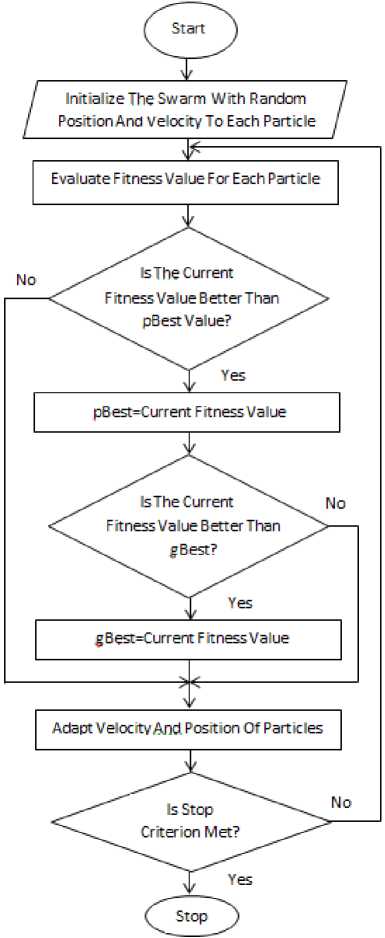
Each particle i has a position vector X / — (x_/1,x_/2, ^,x_/d) , and a velocity vector V / — (v / ₁, V / ₂, ^, V / _d) , where D represents dimension of search space. Similar to the other optimization techniques, PSO requires a fitness function to evaluate performance of each particle. Further, each particle contains a memory to store the best position in the search space ever seen by it. Velocity and position are initialized with random vectors of the corresponding dimension. Trajectory of each particle in the search space is adjusted by updating the velocity, according to the best position attained so far for it, denoted by pB6St , and also the best position gained by any particle in the swarm, denoted by gB6St, so far. The updating rule for the velocity and position of the i ^th particle on dimension d, is as follows:

V /d — wv /d + C 1 r 1d ⁽pB6St /d - % /d )

+ c2r2d(gB6Std-X/d)

max             _T7max

Vd     ,     v/d > Vd max          / т/max

• ^-V d     ,    ^v /d < ^-V d

^X /d ^{— X} /d ^{+ v} /d                                  ⁽⁹⁾

where w is inertia weight that suitable selection of it provides a balance between local and global search ability. c1 And c2 are positive constants that represent the cognitive and social acceleration factors, respectively. rld and Т^д are two uniformly distributed random numbers in the range [0,1] . pBestld denotes the position with the best fitness value, detected so far for the ith particle. gBest Represents the best position obtained by the population. Furthermore ^imax =(vmax , vmax,…,vmax ) represents an upper bound on the absolute amount of the velocity of the ith particle. Fig. 2 indicates the flowchart of the PSO algorithm.

MRSE =(к)

N ___________________

=1 ∑√ezi (i)+6Z2 (i)+eZ3 (i)

where e_Zi ( i ), 6/₂ ( i ), C_l3 ( i ), are the trajectory tracking error of i ^th sample for the first, second and third joint of the robot. N is the number of samples and к is the iteration number.

• V.    Simulation Results

In this section, a numerical simulation for tracking control of a 3-DOF rigid three link manipulator is performed to evaluate the validity of the proposed controller. The numerical values of the robot manipulator parameters are listed in Table 1.

Fig. 2. Flowcharts of particle swarm optimization algorithm [23]

Table 1. Simulation Parameters of Robot

	Mass ( mv , Kg )	Link (Of, m )	Moment of inertia ( 1=1 , Kgm2 )
Joint 1	1.2	0.5	43.33 × 10
Joint 2	1.5	0.4	25.08 × 10
Joint 3	3.0	0.3	32.67 × 10

The desired trajectory to be tracked by links is considered as Qd = *sin( t ) cos( t )sin( t +(Л⁄))+  .

Furthermore external disturbances of       =

0.2 sin(2t),Td2=0.1cos(2t),Td3 = 0.1sin(t)      are applied to the system. Initial position and velocity of the joints are set to zero. According to [27], χ which is called the constriction factor, is defined as follows:

^=„ n . /тг^ т ,

Ф -2+√ Ф² -4                 (11)

=   + Фг , Ф >4

In the PSO algorithm parameters χ , Фт and Фз are set to 0.7298,2.05 and 2.05, respectively. The parameters w , c^ and C2 are defined according to the following equations:

w= Z , Cl = Z Фг , c₂ = Z Фг                 (12)

Gains of the RISE controller are continuously adjusted via PSO algorithm, to minimize the given objective function. Values of tuning parameters of the PSO algorithm are shown in Table 2.

B. Fitness Function

In this section PSO algorithm is applied to the RISE feedback controller for a three rigid link robot manipulator. The objective is to obtain the values of RISE controller gains k_s , Pt and Ct 2 by minimization of the objective function. In this paper, the mean of root of squared error is considered as the cost function, which for i ^th particle is as follows:

Table 2. PSO Tuning Parameters

Parameter	Value
Population Size	20
No. of Iterations (k)	50
^max	3
W	0.7298
Cl	1.4962
C2	1.4962
Lower Bound( ^s , Pt , й?2 )	(0 0 0)
Upper Bound( ks , Pe , «2)	(30 30 30)

The values of the RISE feedback controller gains obtained using PSO algorithm are given in Table 3.

Table 3. Results of Gains Obtained

ks	Pt	«2	Best Cost
25.32	16.7	29.3	0.001139

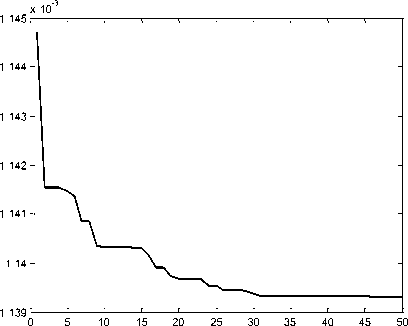
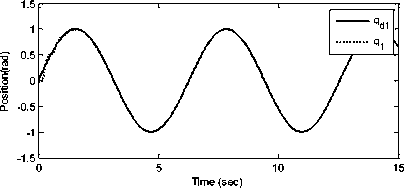
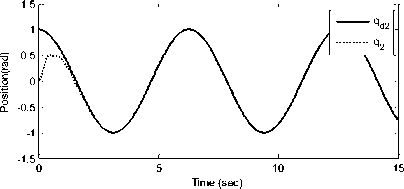
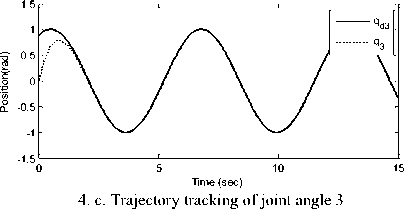
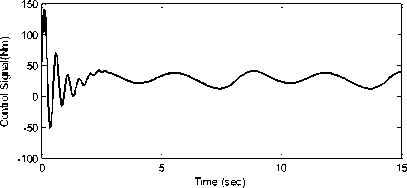
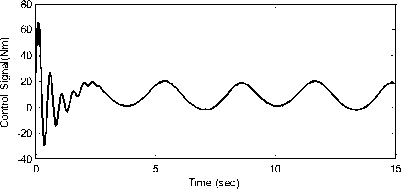
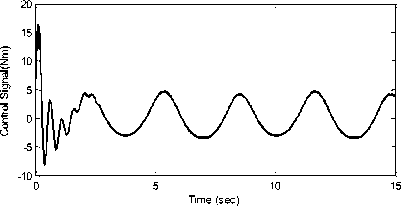
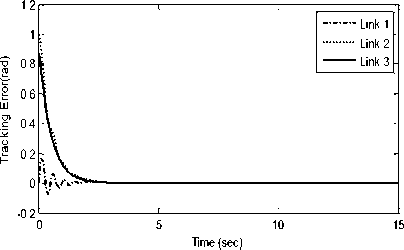
Simulation results are shown in Figs. 3 to 5.

Fig. 3. Fitness function values for 50 iterations

Fig. 3 shows the fitness function trend, which is reduced to find the gain values of the RISE controller.

4. a. Trajectory tracking of joint angle 1

4. b. Trajectory tracking of joint angle 2

4. d. Control effort for joint 1

4. e. Control input for joint 2

4. f. Control input for joint 3

Fig. 4. Tracking position and control input of joints 1, 2 and 3

The trajectory tracking simulation results of all three joints of the robot and their applied corresponding control inputs are shown in Fig. 4. As it can be seen from the figures, the control objective is successfully achieved. Furthermore, the proposed controller generates a continuous control effort, which prevents chattering phenomenon.

Fig. 5. Tracking error of joints 1, 2 and 3

Fig. 5 indicates the position tracking error for all three links of the robot, which confirms that asymptotic tracking is achieved even with the external disturbances.

• VI.    Conclusion

In this paper, a continuous control scheme called RISE feedback is utilized for tracking problem of a 3-DOF rigid three link manipulator. An intelligent tuning of the RISE controller parameters is conducted by using particle swarm optimization algorithm. The controller parameters are adjusted while PSO minimizes the mean of root of squared error. The proposed controller compensates for uncertainties and bounded external disturbances without any chattering in the control input. Simulation results have demonstrated significance of the proposed controller together with the capability to provide an asymptotic tracking performance.