Optimal measurement of dynamically distorted signals

Dynamic measurement theory has appeared and has been developing as a part of inverse problems theory [1]. To investigate short-time signals that tend to appear, say, when spacecraft’s position correction takes place, one of coauthors [2] has recommended measurement transducer (MT) mathematical model, which priory was used within automatic control theory [3].

ж = Ax + Du, у = Cx                          (1)

Here x = x(t) is a vector-function of MT states, x = ($i,$2, • • • ^_n\ и = u(t) and у = y(t^ are vector-functions of measuring signal and observation respectively, и = (ui,^,- ■ • >^m) and у = (yi, y2,..., y_e). Symbols A, D and C denote matrices of MT, and observation unit respectively of order n x n, n x m and I x n. Model (1) appeared to be adequate to mechanical inertia effect of MT, which by itself causes graduation of measured spiked signal u. For the record it becomes an obvious result both of real [4], and numerical experiments [5, 6].

Renewal process of the measurement и by the observation у is ill-posed problem. Thus, to come to solution of this problem there were suggested technically explained hypothesis, as for example, «sliding models» [7] and «МТ regularizability» [8]. Moreover the solution found here «embodied in metall». Meanwhile, [9] by itself offers to investigate finding of the measurement и by observation у by methods of optimal control theory, so that unknown observation minimizes the functional

• 1    „_T

= 52 / iiyW -Уо^н2^                       (2)

9=0

where yo = yo(t) is an observation received by the actual MT, the model of which is the system (1). The minimum of the functional J is sought on a set of admissible measurements, which is constructed itself with regard to existing information (as a rule, incomplete) about unknown observation. In [5, 6] there was recommended an algorithm of numerical solution to the problem (1), (2), which has shown good approximation to exact solution on check example (u = Asin2wt).

But the signal measured often gets distorted not only because of MT mechanical inertia, but also by the fact of mechanical resonances. In the real being MT would be embedded with filters, which could have «cut out» resonant frequency of measured signal. Sometimes these filters provoke resonance but at other frequencies; for this reason there is installed another filters to be able to eliminate resonance arose, etc. This article is about a new model of optimal measurement, in which MT is not only mechanically inertial but resonant as well. The essence of innovation is that the functional (2) has been intruded with one more term, that standed for resonance filters. Thus, as it often happens in virtual cases, the suggested model do not cause secondary resonance.

Except for Introduction this article contains two Parts and References, which are more about tastes and preferences of the authors but completed. In the first Part we describe theoretical investigation of the model, whereas in the second Part we offer numerical algorithm for finding of distorted measurement.

1.    Optimal measurement with regard to interia and resonaces

We consider model MT to be an ordinary differential equations system of the Leontief type (briefly the Leontief type system) [10]

Li = Mx + Du,                            (3)

у = Nx,                                     (4)

where x = (xi,X2, • • . ,x_n) and x = (xx,X2,... ,х_п) are vector-functions of MT states and velocities of MT states changes respectively, L and M denote matrices of order n, corresponding to correlation of states and velocities of states respectively. Moreover we assume that det L = 0, as in another case system (3) it is possible to represent in more simple form. Further, и = (ui,U2,.. ■,u_n) and у = (yi,y2) • • • -Ун) are vector-functions of measurements and observations respectively. We emphasize, that parameters of measurements and observations have more than one, as for example, in the theory of automatic control (1). Naturally, we can not measure parameters more than number of parameters of MT states, but number of measurements and observations parameters is possible to decrease setting equal to zero corresponding components of measurement и = (iq, u^, . • ., u_n) and observation у = (У1,У2, • • • /Уп) vector-functions respectively. Finally, D and N are matrices of order n, characterizing correlation of measurement parameters and connection between MT state and observation respectively. It is clear if some components of vector-function и are equal to zero, then corresponding lines of the matrix N must be completed by zeros. Obviously, model (3), (4) is more general then (1).

The Leontief type systems are finite-dimensioned cases of the Sobolev type equations. Therefore, we shall under investigation use ideas, methods and results of general theory [11, ch. 2], which are adapted to finite-dimensional situation. Following [10], matrix M is called L- regular, if there exists a number a € C such that det(aiL — M) ^ 0. If matrix M is L-regular, then there exists a number p E {0} U N which is equal to zero, if in the point oo L-resolvent (yL — M)^-1 of matrix M has removable singularity; and p is equal to pole order of matrixfunction (yL — M)^-1 in another case. Taking this into account, we will name L-regular matrix M (L,p)-regular, p E {0} U N.

Next, let matrix M be (L,p)-regular, p E {0}UN. For the system (4) we set up the Showalter - Sidorov problem

[R^M)]^p+1(x(Q)-x₀) = Q                         (5)

А.Л. Шестаков, Г.А. Свиридюк under any жо Е R”, а Е pL^M) = {д Е С : det (pL — АГ) / 0}. Here R^(M) = (aL — М)-1 L is right L-resolvent of matrix M. We do not explain preferences of this problem by comparison of the traditional Cauchy problem ж(0) = жо- By opinions a number of authors [12 - 14] the Showalter - Sidorov problem for the Sobolev type equations is more natural then the Cauchy problem, in which it coinsides in the case det L ^ 0. Besides that, preferences of problem (5) in calculations are noted in [5, 6]. Finally point out useful generalization [15] of the problem (5).

Let us fix т € R₊ and introduce into consideration state space X = {ж E L2 ((0, t) , Rⁿ) : x E L2 ((0, r), R”)}, measurement space Я = (u E L2 ((0,r),Rⁿ) : n(^p+1) E L2 ((0, t), Rⁿ)} and observation space 2) — A[X]. There is not always that 2) = X, but it is always that 2) is isomorphic to some subspace in X. Let us separate in Я a closed and convex subset Яд (a set of admissible measurements'), and set of the optimal measurement problem. We shall find a pair (у, и) E 2) x Яд a.e. on (0, t) satisfying to equations (3), (4) under condition (5), and

• 1    T

• a) = min J(v), J(v) = / ||у⁽⁹⁾(<) -Уо^Ц ^dt+ p+i 7

+ E HF_q^\t),u^(t))dt. 0

Here yoft) = fyoift), yc^lf),... , yonto) is an observation obtained on real experiment, i.e. taking down to real MT, model of which is systems (3), (4); || • || is Euclidien norm of the space Rⁿ; v^(t) = fv^\t), v^ft), • • • i^yn4t)) is possible measurement from Яд and its derivatives; F_q E £(Я) is self-adjoint and positive definite operators, q = 0, 1, ..., p + 1, (•, •) is Euclidien scalar product in Rⁿ. We shall name this optimal measurement problem the problem (3) - (6) for brevity.

The problem (3) - (6) in Hilbert spaces and in more general statement (in particular, there had been equired to find the state vector-function ж) was considered in [16] as «rigid optimal control problem». Therefore, we give next result without proof, it is taken from [16] and is adapted to our situation.

Теорема 1. Let matrix M be (L,p)-regular, p E {0} UN, т E R+, with detAf ^ 0. Then for any жо E R”, yo E 2) there exists a unique solution (y,u) E 2) x Яд to the problem (3) - (6), where у = Nx, and

x(t) = lim fc->oo

52 (АГ¹ ((kL^ (M))^p+1-I_n) ьум-¹ (in-(kL^ (M))^p+1) (Du)^4tH q=0

.                    x -1 X fc(p+l)

• 7-    ^— .....- j L ]       ж₀+

к(р +1)  /     /

t - s \ &(р+Т) У

A:(p+1) —1

ц^Г)М) [kLi(M)]p+\Du(s))ds

Let us say that condition detAf ^ 0 does not reduce the generality of the problem under discussion. You can see if matrix M is (L,p) - regular then we turn after replacement ж = e^xtv to equation Lv = (M — XL)v + Du which is at the same form as (3), but det(Af — XL) ^ 0. We note also, that solution (y, a) of the problem (3) - (6) existing by theorem 1 we shall name further the exact solution.

2.    Algorithm of numerical finding of dinamically distorted signals

We restrict ourself to particulare case under construction of our algorithm. In the first place we suppose that т = тг, in the second place we assume that the values of the measurement at the beginning and at the end of the interval [0,r] are equal to zero. Both assumptions simplify the techiques of an algorithm and easily eliminate under passage to general case. Thus, let the matrix M be (L,p)-regular, p E 0 U N, with detM ^ 0. By theorem 1 approximate solution (y^,^) to the problem (3) - (6) we will seek in the form xk^ = E (м^кЬ^М^-К) lYm-1 (^-(кЬ^М^1} фи^^Н g=0 4 x                      /   /         \                      /

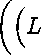
x-i \4p+i)