Optimal Overcurrent Relays Coordination in the Presence Multi TCSC on Power Systems Using BBO Algorithm

Published Online January 2015 in MECS

System protection is an important part in the power network systems. The most important part in designing the protection needs to consider such as the type of relays, the size of circuit breaker and fuse, the type and size of current transformer, the coordination of relays, and them component to maintain the stability of the system. Then to maintain the stability each relay in the power network must setting in proper technique in term of current and time operation. During the operation of modern interconnected power systems, abnormal conditions can frequently occur. Such conditions cause interruption of the supply, and may damage the equipments connected to the system, arising the importance of designing a reliable protective system. In order to achieve such reliability, a back-up protective scheme is provided to act as a second line of defense in case of any failure in the primary protection (the first line of defense). In other words, it should operate after a certain time delay known as CTI, giving the chance for the primary protection to operate.

The fore mentioned situation leads to the formulation of the well-known protective relay setting coordination, that consists of the selection of a suitable setting of each relay such that their fundamental protective function is met under the desirable qualities of protective relaying, namely sensitivity, selectivity, reliability, and speed [1]. Overcurrent relaying, which is simple and economic, is commonly used for providing primary protection (principal) and as secondary (backup) protection in transmission systems [2]. To reduce the power outages, mal-operation of the backup relays should be avoided, and therefore, protection coordination in power networks is a major concern of protection engineer. A relay must get sufficient chance to protect the zone under its primary protection. Only if the primary protection does not clear the fault, the back-up protection should initiate tripping. Each protection relay in the power system needs to be coordinated with the relays protecting the adjacent equipment [3], the overall protection coordination is thus very complicated. Overcurrent relay have two types of settings: pickup current setting and time multiplier setting.

Recently, it is noticeable that the power demand has been increasing substantially worldwide. On the other hand, the expansion of power generation and transmission facilities and equipment has been severely limited due to limited resources and environmental restrictions. As a consequence, some transmission lines are heavily loaded and the system stability becomes a power transfer-limiting factor. FACTS controllers offer many benefits to the network and have been mainly used for solving various power system steady state control problems [4, 5], the impact of the TCSC compensator on distance protection in the presence faults has been reported in [6, 7]. The measured impedance by distance relay for inter phase faults, as well as variation of the measured impedance in inter phase faults, when using TCSC on an adjacent transmission line, are reported in [8], comparing TCSC placements on mid-point and ends of second circuit of double circuit line from distance relay has been reported in [9].

In recent years, many research efforts have been made to achieve optimum protection coordination (optimum solution for relay settings) without TCSC using different optimization techniques, including Random Search (RS) technique is reported in [10], Evolutionary Algorithms (EA) is presented in [11] while Differential Evolution Algorithm (DEA) in [12], Modified Differential Evolution Algorithm (MDEA) in [13], and Self-Adaptive Differential Evolutionary (SADE) algorithm in [14], application Particle Swarm Optimization (PSO) in [15], and Modified Particle Swarm Optimizer in [16, 17], and Evolutionary Particle Swarm Optimization (EPSO) Algorithm in [18], Box-Muller Harmony Search (BMHS) in [19], Zero-one Integer Programming (ZOIP) Approach in [20], Seeker Algorithm (SA) is presented in [21], and Teaching Learning-Based Optimization (TLBO) in [22].

This research paper presents the solution of the coordination problem of IDMT directional overcurrent relays on meshed power system using BBO approach. The problem is formulated as a non linear constrained mono-objective optimization problem. Our goal behind this optimization is to find an optimal setting of Time Dial Setting ( TDS ) and Pickup current ( I P ) of each relay that minimizes the operating time ( T ) of overall relays. The new idea presented in this paper, is taking into account the variation of the effective impedance of the line caused by the action of series compensation devices of the line. Two simulation scenarios with and without multi TCSCs are considered in this paper.

• II.    Apparent Reactance Controlled by TCSC

The TCSC are usually utilized to regulate the voltage at their connection point. The model of these devices and their general model are presented in this section. The compensator TCSC mounted on figure 1.a is a type of series FACTS compensators. It consists of a capacitance ( C ) connected in parallel with an inductance ( L ) controlled by a valve mounted in anti-parallel thyristors conventional ( T 1 and T 2 ) and controlled by an angle of extinction ( α ) is varied between 90° and 180° [23].

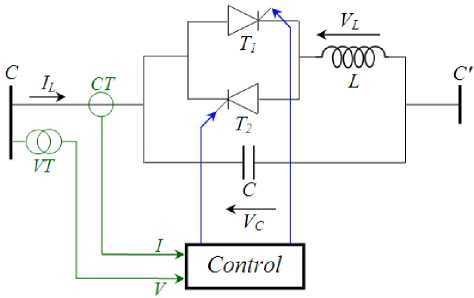
(a)

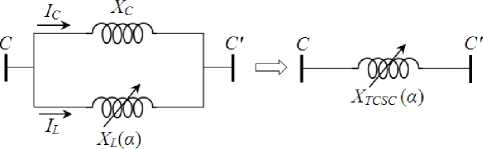
(b)

Fig. 1. Transmission line on presence TCSC system [23]. a). Mounting, b). Apparent reactance.

This compensator injected in the transmission line a variable reactance ( X TCSC ) indicated by figure 1.b. Its value is function of the reactance of the line X L where the device is located. The apparent reactance X TCSC is defined by the following equation [24, 25]:

XTr(Да) = Xr //X, (a) =

TCSC         C     L

X c . X l ( a )

X c + X l ( a )

The expression of X_TCSC is directly related to the angle α , which was varied, following the above equation:

Where,

L max

= L. a

X

L max

n n - 2a - sin(2a)

C

C . to

A part of the “(2),” final the “(1),” becomes:

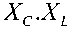
У TCSC

( a ) =

П n - 2a - sin(2a)

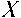
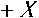
CL

n n - 2.a - sin(2a)

The curve of X TCSC as a function of α is divided into three different regions: inductive, capacitive, and resonance, is summarized in the following figure.

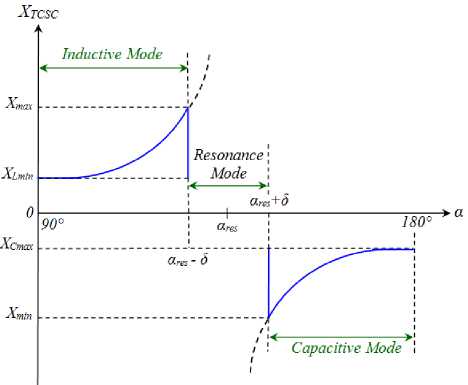
Fig. 2. Characteristic curve X TCSC = f ( α ).

Relay constraints include limits of relay operating time and settings. Coordination constraints are related to the coordination of primary and backup relays.

The operating time of a relay is a function of the pickup current setting and the fault current seen by the relay. Based on the type of relay, the operating time is determined via standard characteristic curves or analytic formula. The bounds on operating time are expressed by:

min

Ti

max ii

Where, T ^min and T ^max are the minimum and maximum operating times of the i^th overcurrent relay.

During the optimization procedure, the coordination time between the primary and the backup relays must be verified. In this paper, the chronometric coordination between the primary and the backup relays is used as follows equation:

The coordination of directional overcurrent relays in a multi-loop system is formulated as an optimization problem. The coordination problem, including objective function and constraints, should satisfy three requirements.

T , - T    > CTI backup     primary

A ． Objective Function

The aim of this function ( f ) is to minimize the total operating time of all overcurrent protection relays in the system with respect to the coordination time constraint between the backup and primary relays.

Where, T backup and T primary are the operating time of the backup relay and the primary relay respectively, CTI is the minimum coordination time interval.

The time dial setting ( TDS ) adjusts the time delay before the relay operates when the fault current reaches a value equal to, or greater than, the pickup current ( I_P ) setting [10-15].

TDS ^min

< TDS, <  TDS max

min            max

IPi — I Pi < IPi

N

f = Min T

I i = 1

Where, T i represents the operating time of the i^th relay, N represents the number of relays in the power system. For each protective relay the operating time T is defined as follows [12-15]:

Where, TDS ^min and TDS ^max are the minimum and the maximum limits of TDS for the i^th relay. I ^min and I ^max are the minimum and the maximum limits of I P for the i^th relay.

T = TDS X

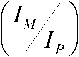
a

в

+ у

Where, T is relay operating time ( sec ), TDS is time dial setting ( sec ), I M is the fault current measured by relay ( A ), I P is pickup current ( A ). The constant α , β , and γ depend on the characteristic curve for IDMT directional overcurrent relay. The current I_M is defined by:

IM

IF KCT

Where, I F is the fault current, and K CT is ratio of the current transformer.

B ． Constraints

The coordination problem has two types of constraints, including the constraints of the relay characteristic and coordination constraints.

BBO is a population based, stochastic optimization technique developed by Pr. Dan Simon in 2008, which is based on the concept of biogeography that deals with nature’s way of distribution of species. Distribution of a species from one place to another is influenced by factors such as rainfall, diversity of vegetation, diversity of topographic features, land area, temperature etc. Areas, where these factors are highly favorable tend to have a larger number of species, compared with a less favorable area. Movement of species from one area to another area facilitates sharing of their features with each other. Owing to this movement, the quality of some species may improve due to exchange of good features with better species. In context of biogeography, a habitat is defined as an Island (area) that is geographically isolated from other Islands. Geographical areas that are well suited as residences for biological species are said to have a high habitat suitability index ( HSI ) [26, 27].

The variables that characterize habitability are called suitability index variables ( SIVs ). SIVs can be considered as the independent variables of the habitat and HSI calculation is carried out using these variables. This addition of good features to low HSI solutions may raise the quality of those solutions. Mathematically the concept of emigration and immigration is represented by a probabilistic model. If P s ( t ) denotes the probability that a habitat contains exactly S species at time t , at time t + A t the probability is:

Ps (t + A t ) = Ps (t )(1 - As A t - Ms A t) +Ps-A-1A t + Ps+A+1A t

Where, λ s and μ s are the immigration and emigration rates when there are S species in the habitat. If time A t is small enough so that the probability of more than one immigration or emigration can be ignored then taking the limit of “(7),” as A t ^ 0 gives the following equation:

'-( A s + M s ) P s + P s ₊ 1 M s + 1 ; S = 0

P s =^

- ( A s + M s ) P s + P s + 1 M s + 1 + P s - 1 M s -p 1 <  S <  S max ⁽¹⁴⁾

"( A s + M s ) P s + P s - 1 M s - 1 ; S = S max

The equation for μ k and λ k for k number of species is derived as per following way:

E . k

M k =

n

Where, E and I are the maximum emigration rate and maximum immigration rate respectively. n is the total number of species in the habitat. When E = I :

A k + M k = E

BBO mainly works based on Migration and Mutation [26-28]:

• A.    Migration

With probability P mod , known as Habitat Modification Probability each solution can be modified based on other solutions. If a given solution S i is selected to be modified, then its immigration rate λ i is used to probabilistically decide whether or not to modify any SIV in that solution.

After selecting any SIV of that solution for modification, emigration rates μ j of other solutions S j ( S j is j - th solution set other than S i , i.e. j ≠ i ) are used to select which solutions among the population set will migrate randomly to chosen SIVs to the selected solution S i . Details about the algorithm of migration are available in [26, 28].

• B.    Mutation

In BBO species count probabilities P_s are used to determine mutation rates.

The probabilities of each species count can be calculated using the differential equation “(14),”. Each habitat member has an associated probability, which indicates the likelihood that it exists as a solution for a given problem. If this probability is very low then that solution is likely to mutate to some other solution. Similarly if the probability of some solution is higher that solution has very little chance to mutate. Mutation rate of each set of solution can be calculated in terms of species count probability using the following equation:

m ( S ) = m_max

1 - P s

max 7

• V. Case Study and Simulation Results

The impact of TCSC on IDMT directional relays coordination is performed on the following two scenarios: without and with multi TCSC (inductive and capacitive operation mode) installed at IEEE 14 bus transmission network [27]. As we mentioned above, the relays coordination problem is formulated as constrained monoobjective problem and solved using the BBO considering 82 decision variables (42 variables represent the I P and 42 variables represent the TDS ).

Figure 3, represents the case study of a network fed by 02 generators and with 14 buses, 20 transmission lines. The transmission network consists of 42 directional overcurrent relays.

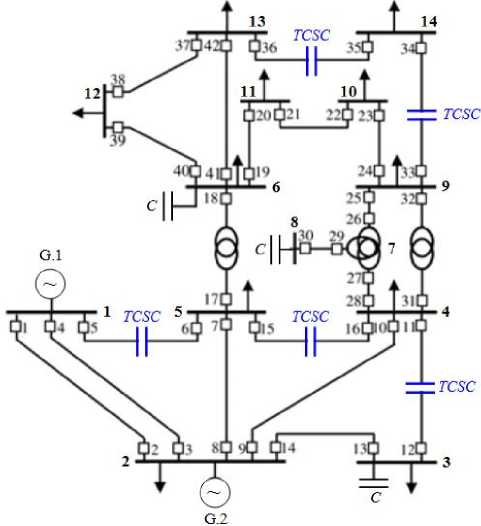
Fig. 3. IEEE 14-bus power system with multi TCSC.

The power system study is compensated with five TCSCs located at middle of the electrical transmission lines (1-5, 3-4, 4-5, 9-14, and 13-14), where compensation degree value K_TCSC = 45 % on capacitive mode and K_TCSC = -25 % on inductive mode for all installed TCSCs.

• A.    Impact of TCSC on CTI

Optimal Overcurrent Relays Coordination in the Presence Multi TCSC on Power Systems            17

Using BBO Algorithm

Table 1 presents, the CTI values of the overcurrent relays without and with multi TCSC on two operation mode (inductive and capacitive).

Table 1. Impact of multi TCSC on CTI value

Primary relay	Backup relay	Without TCSC	With TCSC
			Inductive	Capacitive
5	6	0.3400	-0.3162	-0.2507
11	12	0.3600	-0.8257	-0.7261
15	16	0.3200	-0.5507	-0.2504
33	34	0.3893	-0.7728	-0.4734
35	36	0.3321	-0.4044	-0.2365

From this table, it is clear that all relays are coordinated in the case without TCSC (superior reference value 0,3 sec), but among of them are not coordinated in the presence TCSC (CTI value written in bold). Thus, we can conclude that TCSC causes a loss of coordination between the relays protection line. In this situation, we must compute the new settings of the relays to ensure the coordination.

• B.    Optimal New Setting and Coordination

The optimization constraints for case all study in absence or presence TCSC are:

• >    CTI = 0.3 sec,

• >    50 <  I p < 1700 (A),

• >    0.02 <  TDS < 0.30 (sec),

• >    0.05 <  T i < 1.50 (sec),

• >    Type of curve: very inverse.

The BBO parameters are: P mod = 1.00, n = 0.005, I = 1.00, E = 1.00, m max = 1.00 and Iter max = 300.

The convergence characteristics of the BBO without and with multi TCSCs are depicted in Figure 4. From this figure, we can see that the optimization algorithm is convergence within 270 iterations.

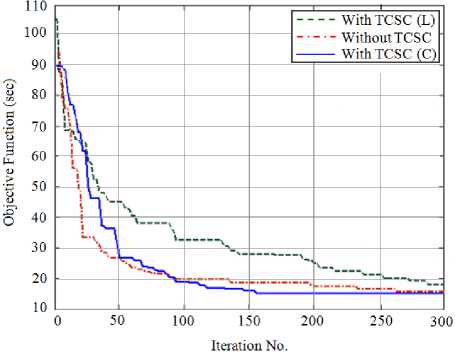
Fig. 4. Convergence characteristics of BBO for all cases.

From this figure, the value of objective function is 15.2147 sec without TCSC, 18.5638 sec with TCSC on inductive operation mode ( L ), and 13,.825 sec with TCSC on capacitive operation mode ( C ).

The optimal settings ( I P and TDS ) for all cases are represented in Tables 2 and 3.

Table 2. Optimal relays settings without multi TCSC

Relay No.	I P (A)	TDS (sec)	Relay No.	I P (A)	TDS (sec)
1	917	0.032	22	550	0.189
2	385	0.044	23	183	0.205
3	385	0.044	24	733	0.236
4	917	0.032	25	440	0.133
5	573	0.075	26	1375	0.150
6	257	0.037	27	257	0.020
7	257	0.055	28	367	0.159
8	344	0.127	29	183	0.046
9	367	0.119	30	825	0.090
10	147	0.103	31	138	0.177
11	367	0.075	32	73	0.048
12	110	0.238	33	733	0.134
13	257	0.067	34	183	0.237
13	573	0.085	35	293	0.137
15	458	0.135	36	550	0.175
16	257	0.175	37	138	0.165
17	413	0.134	38	293	0.143
18	220	0.022	39	110	0.062
19	733	0.202	40	802	0.127
20	293	0.183	41	917	0.170
21	367	0.210	42	293	0.110

Table 3. Optimal relays settings with multi TCSC a). Inductive mode, b). Capacitive mode.

(a)

Relay No.	I P (A)	TDS (sec)	Relay No.	I P (A)	TDS (sec)
1	1119	0.039	22	671	0.230
2	470	0.053	23	224	0.251
3	470	0.053	24	895	0.288
4	1119	0.039	25	537	0.162
5	699	0.092	26	1678	0.183
6	313	0.045	27	313	0.024
7	313	0.067	28	447	0.194
8	419	0.155	29	224	0.056
9	447	0.145	30	1007	0.110
10	179	0.126	31	168	0.217
11	447	0.092	32	89	0.058
12	134	0.290	33	895	0.164
13	313	0.082	34	224	0.289
13	699	0.104	35	358	0.167
15	559	0.165	36	671	0.214
16	313	0.214	37	168	0.202
17	503	0.163	38	358	0.174
18	268	0.027	39	134	0.076
19	895	0.247	40	979	0.154
20	358	0.223	41	1119	0.207
21	447	0.256	42	358	0.134

(b)

Relay No.	I P (A)	TDS (sec)	Relay No.	I P (A)	TDS (sec)
1	843	0.030	22	506	0.174
2	354	0.040	23	169	0.189
3	354	0.040	24	674	0.217
4	843	0.030	25	404	0.122
5	527	0.069	26	1264	0.137
6	236	0.034	27	236	0.018
7	236	0.051	28	337	0.146
8	316	0.117	29	169	0.042
9	337	0.109	30	758	0.083
10	135	0.095	31	126	0.163
11	337	0.069	32	67	0.044
12	101	0.218	33	674	0.124
13	236	0.061	34	169	0.218
13	527	0.078	35	270	0.126
15	421	0.124	36	506	0.161
16	236	0.161	37	126	0.152
17	379	0.123	38	270	0.131
18	202	0.020	39	101	0.057
19	674	0.186	40	737	0.116
20	270	0.168	41	843	0.156
21	337	0.193	42	270	0.101

The new optimal value for coordination between primary and backup relays in the presence multi TCSC is presented in Table 4. After this table that all directional overcurrent relays are well coordinated (superior reference value equal 0.3 sec) after optimization using BBO algorithm.

Table 4. CTI value in the presence multi TCSC after optimization

Primary relay	Backup relay	With TCSC	With multi TCSC
			Inductive	Capacitive
5	6	0,3234	0.3996	0,3373
11	12	0,3126	0.3341	0,4092
15	16	0,3034	0.3300	0,3172
33	34	0,3592	0.3461	0,3253
35	36	0,3219	0.3622	0,3178

• C. Comparison with Published Results

For comparison purpose Table 5, presents a comparison of the best obtained value of the objective function for scenario without TCSC with other published results.

Table 5. Comparison of published results

	MPSO [29]	LP [30]	NLP [30]	NM [30]	BBO
OF (sec)	61.7200	30.8451	18.0099	16.5948	15.2147

From the results of Table 5, it can be also seen that the proposed optimization algorithm (BBO) has given better performance and provides the best solution compared with other results. Figures 5.a and 5.b, present the optimal characteristic curves of directional overcurrent relays number 5 and 6 respectively for all simulation cases.

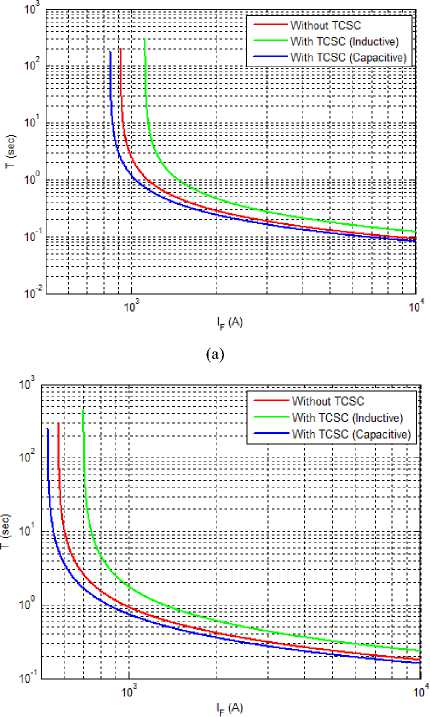
(b)

Fig. 5. Optimal characteristic curves of IDMT relay. a). Relay No. 5, b). Relay No. 6.

From these Figures, we can clearly observe the impact of the two operation mode of TCSC (inductive and capacitive) on the directional overcurrent relays setting.

• VI. Conclusion

In this paper we present an optimal relays coordination in the presence of multiple TCSC on inductive and capacitive operation mode in the transmission power system. We propose the formulation of the relays coordination problem as three scenarios. The obtained results show that the TCSC has a great impact on the setting and the coordination of the numerical directional overcurrent protections. Furthermore, the proposed BBO algorithm show a high efficiency to solve such complex optimization problem, in such a way the coordination of the relays is guaranteed for all simulation scenarios. This last is confirmed with the comparison against other published results.

We conclude also that the constraint violation handling methodology is well formulated and provides only feasible solutions. Moreover, the obtained optimal setting and coordination of overcurrent relays for each compensation degree could be used by the operating system (OS) of practical power system to ensure an offline setting and coordination of these relays in function with the compensation degree of the line.

The continuity of this work will be the coordination of the overcurrent relays in the presence of series FACTS devices considering several conflicting objective functions and various power system topologies using multi-objective, hybrid optimization algorithms and multi agent.

• [1]    P.M. Anderson, “Power System Protection” , published by McGraw-Hill, New York, USA, 1999.

• [2]    A.Y. Abdelaziz, H.E.A. Talaat, A.I. Nosseir, and A.A. Hajjar, “An Adaptive Protection Scheme for Optimal Coordination of Overcurrent Relays”, Electrical Power System Research , Vol.61, No.1, pp. 1-9, 2002.

• [3]    H. Zeienldin, E.F. El-Saadany, and M.A. Salama, “A Novel Problem Formulation for Directional Overcurrent Relay Coordination”, IEEE Large Engineering Systems Conference on Power Engineering (LESCOPE) , Halifax, Nova Scotia , Canada, 28-30 July, 2004.

• [4]    K.K. Sen, and M.L. Sen, “Introduction to FACTS Controllers: Theory, Modeling and Applications” , John Wiley & Sons, Inc., and IEEE Press, USA, 2009.

• [5]    X.P. Zhang, C. Rehtanz, and B. Pal, “Flexible AC Transmission Systems: Modelling and Control” , Springer Publishers, Heidelberg - Germany, 2006.

• [6]    M. Khederzadeh , T.S. Sidhu, “Impact of TCSC on the Protection of Transmission Lines”, IEEE Transactions on Power Delivery, vol. 21, no. 1, pp. 80-87, January 2006.

• [7]    S. Jamali, A. Kazemi, and H. Shateri, “Measured Impedance by Distance Relay for Inter Phase Faults with TCSC on a Double Circuit Line”, 18^th Australasian Universities Power Engineering Conference (AUPEC) , Sydney, Australia, 14-17 December 2008.

• [8]    S. Jamali, A. Kazemi, and H. Shateri, “Measured Impedance by Distance Relay for Inter Phase Faults in Presence of TCSC on Next Line”, IEEE Region 10 Conference (TENCON) , India, 19-21 November 2008.

• [9]    S. Jamali, A. Kazemi, H. Shateri, “Comparing TCSC Placements on Mid-point and Ends of Second Circuit of Double Circuit Line from Measured Impedance Point of View”, IEEE/PES Transmission and Distribution Conference and Exposition , Chicago - USA, 21-24 April 2008.

• [10]    D. Birla, R. Prakash, H. Om, K. Deep, and M. Thakur, “Application of Random Search Technique in Directional Overcurrent Relay Coordination”, International Journal of Emerging Electrical Power Systems , Vol. 7, No. 1, pp. 114, 2006.

• [11]    J.A. Sueiro, E. Diaz-Dorado, E. Míguez, and J. Cidrás, “Coordination of Directional Overcurrent Relay using Evolutionary Algorithm and Linear Programming”, International Journal of Electrical Power and Energy Systems , Vol. 42, pp. 299-305, 2012.

• [12]    R. Thangaraj, T.R. Chelliah, and M. Pant, “Overcurrent Relay Coordination by Differential Evolution Algorithm”, IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES) , India, December16-19, 2012.

• [13]    R. Thangaraj, M. Pant, and K. Deep, “Optimal Coordination of Overcurrent Relays using Modified Differential Evolution Algorithms”, Engineering

  Applications of Artificial Intelligence , Vol. 23, No. 5, pp.820-829, 2010.

• [14]    M. Mohseni, A. Afroomand, and F. Mohsenipour, “Optimum Coordination of Overcurrent Relays Using SADE Algorithm”, 16^th Conference on Electrical Power Distribution Networks (EPDC) , Bandar Abbas, Iran, 19-20 April, 2011.

• [15]    M.R. Asadi, and S.M. Kouhsari, “Optimal Overcurrent Relays Coordination using Particle Swarm Optimization Algorithm”, IEEE/PES Power Systems Conference and Exposition (PSCE) , Seattle, USA, 15-18 March, 2009.

• [16]    H. Zeineldin, E. El-Saadany, and M. Salama, “Optimal Coordination of Overcurrent Relays using a Modified Particle Swarm Optimization”, Electrical Power Systems Research , Vol. 76, No. 11, pp. 988-995, 2006.

• [17]    M.M. Mansour, S.F. Mekhamer & N.E.S. El-Kharbawe, “A Modified Particle Swarm Optimizer for the Coordination of Directional Overcurrent Relays”, IEEE Transactions on Power Delivery , Vol. 22, No. 3, pp. 14001410, 2007.

• [18]    H. Leite, J. Barros, and V. Miranda, “The Evolutionary Algorithm EPSO to Coordinate Directional Overcurrent Relays”,    10^th  IET International Conference on

  Developments in Power System Protection (DPSP) , Manchester, UK, March 29 - April 1, 2010.

• [19]    A. Fetanat, G. Shafipour, and F. Ghanatir, “Box-Muller Harmony Search Algorithm for Optimal Coordination of Directional Overcurrent Relays in Power System”, Scientific Research and Essays , Vol. 6, No. 19, pp. 40794090, 2011.

• [20]    J. Moirangthem, S.S. Dash, and R. Ramaswami, “Zero-one Integer Programming Approach to Determine the Minimum Break Point Set in Multi-loop and Parallel Networks”, Journal of Electrical Engineering & Technology (IJET) , Vol.7, No.2, pp. 151-156, 2012.

• [21]    T. Amraee, “Coordination of Directional Overcurrent Relays Using Seeker Algorithm”, IEEE Transactions on Power Delivery , Vol. 27, No. 3, pp. 1415-1422, 2012.

• [22]    M. Singh, B.K. Panigrahi, and A.R. Abhyankar, “Optimal Coordination of Directional Overcurrent Relays using Teaching Learning-Based Optimization (TLBO) Algorithm”, International Journal of Electrical Power and Energy Systems , Vol. 50, pp. 33-41, 2013.

• [23]    M. Zellagui, and A. Chaghi, “Impact of TCSC on Measured Impedance by MHO Distance Relay on 400 kV Algerian Transmission Line in Presence of Phase to Earth Fault”, Journal of Electrical Systems (JES) , Vol. 8, No. 3, pp. 273-291, September 2012.

• [24]    M. Zellagui, and A. Chaghi, “A Comparative Study of Impact Series FACTS Devices on Distance Relay Setting in 400 kV Transmission Line”, Journal of Electrical and Electronics Engineering (JEEE) , Vol. 5, No. 2, pp. 111116, October 2012.

• [25]    M. Zellagui, and A. Chaghi, “Impact of TCSC on Distance Protection Setting based Modified Particle Swarm Optimization Techniques”, International Journal of Intelligent Systems and Applications (IJISA) , Vol. 5, No. 6, pp. 12-24, 2013.

• [26]    D. Simon, “Biogeography-Based Optimization”, IEEE Transactions on Evolutionary Computation , Vol. 12, No.6, pp. 702-713, 2008.

• [27]    D. Simon, “A Dynamic System Model of BiogeographyBased Optimization”, Applied Soft Computing , Vol. 11, No. 8, pp. 5652-5661, 2011.

• [28]    A. Bhattacharya, and P. K. Chattopadhyay, ^“Application of Biogeography-Based Optimization for Solving Multiobjective Economic Emission Load Dispatch Problems”,

  Power Components and Systems , Vol. 38, No.3, pp. 340365, 2010.

• [29]    H.H. Zeineldin, E.F. El-Saadany, and M.M.A. Salama, “Optimal Coordination of Overcurrent Relays using a Modified Particle Swarm Optimization”, Electric Power Systems Research , Vol. 76, pp. 988-995, 2006.

• [30]    M. Ezzeddine, R. Kaczmarek, and M.U. Iftikhar, “Coordination of Directional Overcurrent Relays using a Novel Method to Select their Settings”, IET Generation, Transmission & Distribution , Vol.5, No.7, pp. 743-750, 2011.

Institute of Algiers, Algeria in 1991, 1994 and 2004 respectively. Since January 1993, he has been with the University of Sciences and Technology Houari Boumediene (USTHB) of Algiers, Algeria as a teacher and researcher and a Fulbright Fellowship during 2005-2006 in the University of Washington (Seattle, USA). He is now an associate professor in U.S.T.H.B. and the Director of the Industrial and Electrical Systems Research Laboratory (LSEI) since 2007. Pr. Boudour is senior member of Institute of Electrical and Electronics Engineers (IEEE), USA, and president of PES chapter in IEEE Algeria subsection. His main interests are power systems stability, security assessment, control, optimization, power system protection, application of intelligent and metaheuristic in electrical engineering.