Optimal Power Flow Solution using Efficient Sine Cosine Optimization Algorithm
Автор: Abdelmoumene Messaoudi, Mohamed Belkacemi
Журнал: International Journal of Intelligent Systems and Applications @ijisa
Статья в выпуске: 2 vol.12, 2020 года.
Бесплатный доступ
The problem encountered in most metaheuristic methods is the choice of the good control parameters of the algorithm. That is the objective of this work by using an efficient sine cosine algorithm (ESCA) in optimal power flow problem. The sine-cosine algorithm (SCA) is a modern method applied in numerical optimization problems. It consists of search randomly the best vector of control variables from the initial group of elements and oscillates to converge to the global optimum or diverge from it, functioning with a simple formulation based on sine and cosine mathematical functions with few setting parameters. In the proposed efficient sine cosine Algorithm (ESCA) the best values of setting parameters are chosen to give the best optimum solution with fast convergence. This technique improves the quality of the solution by exploring more search domain than the SCA method. The modified algorithm has been applied to the classical IEEE 30-Bus network with various objective functions and constraints. To make the comparison of ESCA and different recent algorithms, present results show the importance of ESCA to give the best and effective solution to the multi-objective optimal power flow problem.
Optimal power flow (OPF), load flow (LF), sine cosine Algorithm (SCA), efficient SCA (ESCA), fuel cost, real power losses
Короткий адрес: https://sciup.org/15017493
IDR: 15017493 | DOI: 10.5815/ijisa.2020.02.04
Текст научной статьи Optimal Power Flow Solution using Efficient Sine Cosine Optimization Algorithm
Published Online April 2020 in MECS
Nowadays, optimal power flow (OPF) is an essential field in modern power systems market and investment. The major goal of the optimal power flow is to reduce some types of objective functions under conditions that are some constraints are respected, in order to determine the set of setting variables in the power network. The equality constraint is the equilibrium state of power systems represented by power flow equations to check the equality between the generation and the demand. The feasible range of all variables to ensure security and operation conditions which represent the inequality constraints. The variables which are changed in the optimization process to give the optimal solution are called the variables of control. The active generator powers in generating bus except in slack bus (PV buses), voltage amplitudes in generating unit, transformer regulating ratios and reactive power of shuntcompensator are cited among the set of variables of control.
Whereas, the states variables are found by the state of power systems and are depend on variables of control among them we listed the active generator power of slack bus, amplitude voltages in load bus (PQ buses), the phase angles in PV and PQ buses, the generator reactive powers, and the apparent power flow in transmission line. Consequently, the combination of the constraints and all variables with certain objectives function the OPF problem convert to the non-smooth, non-convex and nonlinear optimization problem.
After the modeling of the optimal power flow problem, the optimization of the OPF becomes easy by applying appropriate methods. For this, there are classical methods and metaheuristic methods. Various classical algorithms are applied to solve the problem of the optimal power flow (OPF). These algorithms include traditional linear and nonlinear methods. Nonlinear methods include: reduced gradient method, Newton method, successive quadratic method and interior point method which is the newest and the most effective method. All these methods are based on Lagrange formulation and the condition of Kurush and Kuhn-Tucker[1-4]. Although, they are precise and fast but require several calculations and converge almost to the local optima for non-convex cost function. Recently, standard meta-heuristic methods are used in the OPF problem based on stochastic intelligence techniques of agents in the group, which are applied for the global solution. The most important methods are the genetic algorithm (GA) and improved GA [4-8], evolutionary programming (EP) [9], improved evolutionary programming (IEP) [10]. Additionally, The application of particle swarm method (PSO) [11], parallel processing with PSO (PPPSO) and differential evolution (DE)[13] are used to solve large OPF problem. Novel meta-heuristic methods inspired by physical laws and behavior of animals and insects in nature are widely used for solving the OPF problem. Among them they are shuffled frog leaping algorithm (SFLA) [14],gravitational search algorithm (GSA)[15,16], biogeography-based optimization (BBO)[17], harmony search algorithm (HS) and improved harmony search algorithm (IHS)[18-20], artificial bee colony algorithm (ABC) [21],differential search algorithm (DSA)[22,23], teaching-learning-based optimization technique (TLBO)[24], krill herd algorithm (KHA)[25], improved electromagnetism-like mechanism method (IELM)[26], improved colliding bodies optimization algorithm(ICBO)[27], black-hole-based optimization (BHBO)[28], Firefly algorithm[29], Grey Wolf Optimizer (GWO) [30], Jaya Algorithm (JA) [31], moth swarm algorithm (MSA)[32] and Enhanced Flower Pollination Algorithm (EFPA)[33].
Most of these methods are applied to solve the OPF problem with convex, non-convex, non-smooth cost functions and other objectives such as voltage profile improved and voltage stability enhancement. They exist other improved methods to enhance the convergence and solution such as oppositional and quasi-oppositional biogeography-based optimization (OBBO, QOBBO)[34,35], quasi-oppositional Jaya algorithm (QOJA) [36], the combination of the particle swarm and gravitational search method (PSOGSA) developed in [37]. Also, the combination of Differential evolution and Harmony search algorithm (DEHS) [38]. In [39] a differential evolution algorithm integrated with different handling techniques with self-adaptive penalty (SP) as the better and an ensemble of the constraint handling are used to improve the solution of the multi-objective optimal power flow.
The main problem encountered in the meta-heuristic algorithms is the convergence to the worst global optima, thus it is due to the worst choice of the appropriate setting parameters. In the present paper, an efficient sine cosine algorithm (ESCA) is applied to solve the optimal power flow problem. The sine-cosine algorithm (SCA) is a novel meta-heuristic method uses sine and cosine formulation for each generation to reach the optimal solution, first was developed and detailed by Mirjalili [40]. In [41] a sine-cosine algorithm and modified sine cosine with levy flights are added to the original sinecosine algorithm have been detailed for optimizing the multi-objective OPF to enhance the convergence to the global optimum. But, the improved SCA is difficult compared to the standard SCA method, which is a simple and works with few parameters with simple formulation of updating the position of individuals in the group. In this paper, the appropriate parameters of (SCA) are chosen to improve the quality of the solution and accelerate the convergence to the best global optimum.
Various types of objective functions have been optimized by ESCA method on standard IEEE 30bus. In order to validate the results, a discussion and a comparison have been achieved with other meta-heuristic methods. Consequently, this technique improves greatly the quality of the solution and the rapidity of the convergence.
The organization of this paper is detailed as flow: an introduction in section I. Problem Formulation with different types of objective function of optimal power flow is modeled in section II. The details of SCA and ESCA with modified parameters are given in section III.
In section IV a numerical results with comparison are discussed in section V. Finally, a conclusion is showed for evaluating this work.
-
II. Problem Formulation
By the combination of different objective and constraint with all variables the OPF problem can take the following form:
Minimize F(s, u)(1)
subject to G(s, u)(2)
and H(5,u) < 0(3)
Where F(s,u) is the objective function, G(s,u) is the equality and H(s,u) is the inequality constraints. S is the vector of state variables and U is the vector of control variables, the two vectors are given by:
S = ( Pg , 2 ,..' П n , V I i ’-V L^ Q g x ,Q gne , S L i ,", S L nbr ) (4)
Where P gslack is the slack active generator power, 0 the angle of PV and PQ buses, VL the amplitude voltages of PQ buses, Q g the reactive powers in generator and the SL is the apparent power in transmission lines.
We denote by P g : the active powers in PV buses, V g : the amplitude voltages of generators, T : the regulating transformers ratios and Qc reactive power of shunt compensators.
The number of buses, the number of PQ buses, the number of generators, the number of tap transformers, the number of shunt compensators and the number of lines are denoted by n,nl, ng, nt ,nc , nbr respectively .
-
A. Objective Function Types
Many objectives functions are studied to ensure the goal of the optimal power flow problem. Most of the objective functions are detailed in the next section:
-
a. Production Fuel Cost
The main objective function in the OPF problem is the total production cost caused by the fuel used in the unit of generation:
ng
F c = £ C i (P)
i = 1
NL
F v = F + ® v £ V - 1
i = 1
Where C i : is the production cost of thermal unit n i given in simple convex and smooth quadratic model which is given by:
C i ( P gi ) = a i + b i P gi + cP (7)
Where: P gi is the generator active power at unit i and a i , b i and c i are the cost coefficients of ith unit.
For multi quadratic model, the fuel cost takes multi function for each interval of generating power which explained by using of multiple fuel form the unit. The problem for this type becomes a non-convex optimization problem. The production cost in (6) is expressed by the following model:
|
a i1 |
+ b i1 P gi + C i 1 Pgi |
if |
min gi gi gi 1 |
|
|
C i ( P gi ) = |
ai 2 ... |
+ b ,2 P gi + C i 2 P g 2 |
if |
P .. < P . < P ... zox J gi 1 -i gi -i gi 2 (8) |
|
. a im |
2 im gi im gi |
if |
max gi ( m - 1) - gi - gi |
Where: a im ,b im and c im are the cost coefficients of fuel type m in the ith unit.
To increase the efficiency of generating unit a number of admission valves are added and switched successively causing fluctuation form in the function. The effect of these valves is appeared by addition of sine component in the cost function; therefore this model converts to the non-smooth cost function. Then the model of cost with the effects of valves is given by the equation:
C i ( P gi ) = a i + b i P gi + c . P 2 + | e i x sin( ft(P gi min - P gi )| (9)
Where: e i and f i the coefficients of the sine components of the valves.
-
b. Active Power Loss
The minimization of the total active power loss in the power network is essential which caused by the bad effect of the reactive power circulation. Consequently, the total active power loss can be formulated as follows:
F l = £ g k (V 2 + V j - 2-- cos e j ) (10)
k e Nbr
Where g k : is the real part of admittance of the line (i-j), n br : is the total number of electric lines in power systems.
-
c. Voltage Deviation Improvement
Sometimes, it is desirable that the voltage should be close to a nominal value (1p.u.), which is reflected by the reduction of the voltage amplitude deviation at load buses. Then the objectives function for both the fuel cost and the voltage deviation convert to:
-
d. Voltage Stability Enhancement
The improvement of the voltage stability is achieved by minimizing the stability index L of load buses. This objective is attained by minimizing the global maximum index L max :
Lmax = max {Lk } , k e npq
We define the index Lk of load bus k:
L k =
1 + Vk-V k
V ok : is the voltage of bus without load:
Ng
V =-V H V(14)
ok2
i = 1
H 2 is a matrix defined by partial inversion of admittance matrix of orderly Y bus to PQ, PV buses, and then we have:
h 2 =- y;Y (15)
Finally, the objective function of this problem is formulated by:
F = F + ^ L^ (16)
SL max
Where: ω L is a weighting factor of voltage stability.
-
B. Equality Constraint
The equality constraint describes the equilibrium state of the system during the optimization process. It can resolve by Newton Raphson load flow equation to find all state variables. These variables confirmed the balance equation which is the production power equal the demand power plus losses.
n g
£ P gi = P d + P L (17)
i = 1
-
C. Inequality Constraints
To ensure the good operation of equipment in the power system, it must keep certain variables in their limits which are represented by h(s,u). Among them we list the generated active and reactive powers; the bus voltage magnitudes of all buses, the transformers tap settings and the compensators reactive powers:
P„__
gi min gi gi max , g
О ™ < О < О ™ Jen gimin gi gimax , g
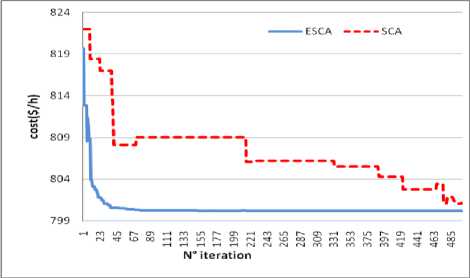
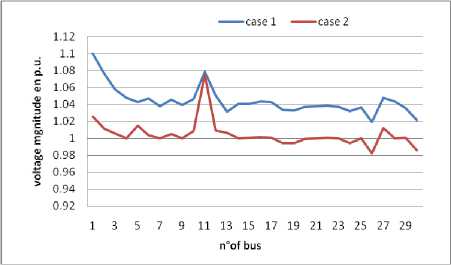
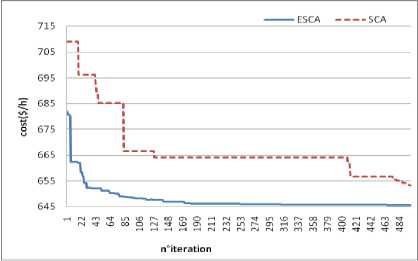
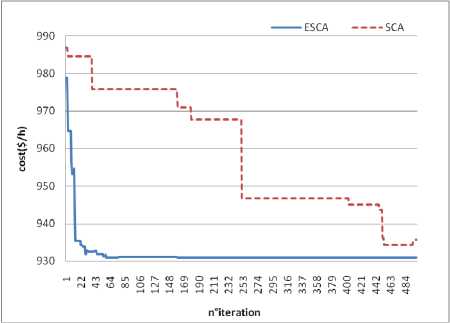
V-- Ti min < Ti^ Ti i e nt Line power flow constraints: the constraint of transmission lines loading is given by: Sl,< Smx, i e nbr (19) D. Global Objective function In meta-heuristic search algorithms, all control variables remain within their limits except the slack bus active power. We add the inequality constraints related to the state variables to the objective function by multiplying with penalty factors. Therefore, the augmented or fitness function form of the objective function becomes: nl FT = F + kp(P -P .)2 + kv2(V - V, i=1 ng nbr +kq 2 (Qgi- Qgm)2 + ks 2 (Sli- SD2 i=1 xk+1 Where: kp ,kv ,kq and ks are the penalty factors Pglismlack Vilimand Qglim are defined as: lim minmin 1 gslack 1 gslack lvr 1 gslack < 1 gslack lim maxmax pgslack pgslack for Pgslack > pgslack < Vllm= Vmin for V< V Vlug = VimaxforVi > V min max Qgirn = Qmn foQ< Qmn Q' = Qmax NQg> Qgmax g g gg F is the total cost function given by (6), real power losses given by (10), cost with voltage profile given by (11), or F of total cost with voltage stability is given by (16). The equality constraint is solved by Newton-Raphson load flow equation. Sine Cosine Optimization Algorithm (SCA) is a global optimization Algorithm was introduced and detailed by Mirjalili [40]. Its principle process consists of searching stochastically the best vector of control variables from an initial group of members and converges to the best solution in the search space or diverges from it in fluctuating manner, using a simple mathematical formulation based on sine and cosine functions. Compared to other methods, the SCA method has a few control parameters and easy to implement. Whereas SCA works on a group in which the members move by changing their positions and converge to the optimal solution in the feasible domain. The number of members in the group is np and the initial population of the SCA is randomly generated within the feasible ranges of control variables. Each member adjusts its position to the best destination using sine and cosine formulation. In the SCA a member is represented by the vector Xi = Xij ,i enp,jend which their elements represent the variables of control. The reverse operation for calculating the objective function and determining the elements of control variables we put Uj = Xi,j,i e np; j e nd. In the optimization process, the destination Xgbest = C^gbest,....xgbest; represents the best member which has the best fitness function among all the members in the group. The updated position of member n°i modified under the following equation: xk + r1 xsin(r2)x |r3Xgbestk -xik|; r4^ 0.5 xk + r1 x cos(r2) x r3Xgbestk - xk ; r4 > 0.5 Where: xiK : is the position of the current solution at kth iteration, r2,r3,r4 are random parameters in the range of [0,2^] ,[0,2] [0,1] respectively. Xgbestk : The best position or destination of the group until iteration k. r1 is an iterative adaptation parameter (conversion parameter) decreases from a to 0 with the number of iteration increase from 0 to kmax and was given by the following expression: Where a: is a constant parameter and kmax is the maximum number of iterations. The parameter r1 describes the movement of the individual in the next position. Thus if r1 <1 the updated individual is situated in the region between the previous position and the best vector (destination) else the updating vector is situated outside. The parameter r2 is designed to measure the distance of movement of convergence or divergence to the destination. The parameter r3 is a weighting factor to adjust the destination, rather than it is an important parameter and defines the speed of convergence and the quality of the solution to the best agent. The parameter r4 is the random value which its role is to change the use of sine or cosine component such as in equation (22). A. Efficient SCA To improve the SCA algorithm for the best global solution with speed convergence, it should to choose the appropriate parameters of the SCA algorithm. In standard SCA the control parameters r2 and r3 take the value r2 = 2* n *rand[0,1]and r3 = 2*rand[0,1] respectively. Where rand [0,1] is a random number in range [0, 1], r1 is given by equation (23). In the efficient ESCA the optimal parameters are modified as follow: The parameter r1 take random value in interval [0, 2] then we set r1=2*rand[0,1], r3 take a constant value which equal to r3=1 to accelerate the convergence, r2 is not changed. The steps of the algorithm are listed in the following section. B. Algorithm of ESCA and SCA ESCA and SCA have the same steps of the algorithm; the difference appears in the choice of setting parameters. The main steps of ESCA and SCA algorithms are detailed as follow: 1- Initialize randomly np vectors between the limits of control variables U by the following expression: x0. = umin + rand * (umax- um^) (24) Where ienP,jend and umax,uminare lower and upper limits of control variables respectively. Rand is a random number in interval of [0, 1]. 2- Set Xi = Xi0and the iteration counter to k=1. 3- The fitness function of all elements Xi are determined using global function F (eq. 20) and select the destination Xgbest the best element which has the best value among elements X, where i e nP 4- Update the parameters: rj, r2, r3, r4 for each element of Xi 5- Change the position of the actual member Xi using SCA updating equation (22), and determine the new elements Xi 6- Check the test limits, if the elements of Xi violate the upper or lower bound of control variables; it must take this upper or lower bound. 7- If k < kmax set k=k+1 and go to step 3 otherwise go to step 8. 8- Take Ucpt = Xgbest and run load flow to calculate real slack power, other elements of state variables, fuel cost and active power losses. For evaluating the global function for each iteration, it must solve the power flow equation which is the equality constraint. After that all state variables, active power losses are found and the process of optimization is continued. In order to validate the application of the ESCA compared to SCA algorithm, we consider the standard IEEE 30-bus with 41 branch systems [2] for minimizing various functions. The dimension of the vector of control variables is nd =24 which includes 5 generator-bus active power, 6 generator-bus voltage magnitudes, 4 transformer-tap settings, and 9 bus shunt reactive compensators. The bus n°1 is chosen as the slack bus, 2, 5, 8, 11 and 13 are chosen as PV buses and the rest are PQ (load) buses. The cost and active power loss of initial load flow base case are 901.8 $/h and 5.8 MW respectively. The permissible ranges of transformer tap settings are 0.9p.u and 1.1 p.u respectively, the permissible ranges of generator bus voltage are 0.95 p.u and 1.1 p.u respectively, and the permissible ranges of load bus(PQ buses) voltage are 0.95p.u and 1.05 p.u respectively. The permissible ranges of reactive power of shunt compensators are 0 p.u and 0.05 p.u. The coefficients of the fuel cost functions and the permissible ranges of the real power of generators are given in table 1. Table 1.Generators Cost coefficients and generators active power limits Real Power output Limit(MW) Cost coefficients Bus N° Min. Max. a($/h) b( $/MWh) c($/(Mw)2h) 1 50 200 0 2.00 0.00375 2 20 80 0 1.75 0.01750 5 15 50 0 1.00 0.06250 8 10 35 0 3.25 0.00834 11 10 30 0 3.00 0.02500 13 12 40 0 3.00 0.02500 The population size in ESCA and SCA is equal to 50. For each problem types, we choose kmax=500 which is the maximum number of iterations. The constant parameter a in equation (23) of r1 is a=1.5 for standard SCA algorithm. Table 2 and table 5 show the OPF results obtained by the proposed ESCA method for various types of functions. Simple fuel cost, fuel cost with voltage profile improvement, fuel cost with voltage stability and total real power losses are minimized by ESCA and SCA. Also, other types of non-convex and non-smooth fuel cost are optimized such as the cost with the different type of fuels and fuel cost with valves effects. To obtain the best global optimum several executions of the ESCA method have been achieved for each type of functions. The results listed in table 2 and table 5 is the best solution of the ESCA method. A. Type1: Simple Production Cost Function The first simulated type of optimization is the minimization of simple quadratic fuel function which is given by equation (6) and introduced in augmented objective function given by equation (20) to respect all constraints. The results obtained by ESCA are listed in type 1 of table 2 of which give the fuel cost of 800.2198 $/h with the voltage deviation of Vd=0.9454 p.u. The characteristic of convergence of ESCA compared to the SCA is shown in figure 1. From the results and figure of convergence of simple fuel cost function which is a convex function, it is clear that the ESCA is converged fast than SCA to the best global optimum. The inequality constraints of all variables are respected and all variables remained in their permissible ranges. Fig.1. Convergence characteristics of SCA and ESCA algorithms of Type 1. Table 2. Simulation results with ESCA of types 1,2 and 3. Control variables Type 1 Type 2 Type3 Pg1(MW) 177.6493 177.1922 177.1127 Pg2(MW) 48.6658 49.3761 48.8634 Pg5(MW) 21.3344 21.8592 21.3803 Pg8(MW) 20.9348 23.2242 21.2303 Pg11(MW) 11.8018 10.0000 11.8190 Pg13(MW) 12.0000 12.0000 12.0000 V1(pu) 1.1000 1.0254 1.0867 V2(pu) 1.0767 1.0113 1.0681 V5(pu) 1.0430 1.0146 1.0389 V8(pu) 1.0457 1.0051 1.0460 V11(pu) 1.0788 1.0745 1.0630 V13(pu) 1.0313 1.006 1.0569 T4,12 0.9456 0.9688 0.9922 T6,9 1.0603 1.1000 0.9720 T6,10 0.9332 0.9000 1.1000 T28,27 0.9809 0.9718 0.9682 Q10 (pu) 0.0500 0.0500 0.05 Q12(pu) 0.0000 0.0000 0.05 Q15(pu) 0.0500 0.0500 0.05 Q17(pu) 0.0500 0.0000 0.05 Q20(pu) 0.0413 0.0500 0.05 Q21(pu) 0.0500 0.0500 0.05 Q23(pu) 0.0304 0.0500 0.05 Q24(pu) 0.0500 0.0500 0.05 Q29(pu) 0.0258 0.0277 0.05 Cost ($/h) 800.2198 804.9968 800.4102 Active Losses (MW) 8.9861 10.2517 9.0057 Vd(pu) 0.9454 0.09163 0.9774 Lmax 0.1267 0.1367 0.1224 The results of proposed ESCA are compared only with other solutions reported in the literature. The comparison of results is shown in Table 3. ESCA gives a good global minimum compared to other meta-heuristic methods reported in the literature such as (JA)[31], Moth swarm algorithm (MSA)[32], superiority of feasibly solutions differential evolution (SF-DE) [39], sine cosine algorithm (SCA)[41], modified SCA (MSCA) [41]which give 800.41 $/hr, 800.660 $/h, 800.3887$/h, 801.410$/h, 800.4985$/h, 800.4794$/h, 800.5099$/hr, 800.4131$/hr, 800.1020$/hr, 799.3100 $/hr respectively. It is observed that ESCA gives the best value of cost than other methods with an acceptable value of Vd. SCA[41] MSCA[41] give a minimum values than ESCA with the important values of Vd which are 2.0825 p.u and 1.4246 p.u. respectively. The important value of Vd represents the most violations of voltage limits in load (PQ) buses which is infeasible solution. B. Type 2: Cost with Voltage Profile In type 2, both the fuel cost and voltage profile are considered for the minimization, for the reason to improve the quality of service by reduced voltage margin. This type of function is given by equation (11) and (20). The results after the optimization of all control variables and functions are listed in table 2 type 2 of ESCA results. The production cost provided by the proposed ESCA is 804.9968 $/h with voltage deviation Vd=0.09163 p.u. It is clear that the voltage deviation of PQ buses Vd is greatly improved by using ESCA than SCA[41], MSCA[41] which give 0.1082 p.u. and 0.1030 p.u. respectively. We observe that the voltage deviation Vd obtained in case 2 is reduced than the Vd obtained from case 1. Diagram of voltage amplitudes for all buses of type 1 compared to type 2 obtained by ESCA is illustrated in Figure 2. It is clear that the voltage magnitudes in PQ buses approach to 1 p.u. of case 2. For the comparison with other methods such as: PSO[11], DSA [23]; GWO[30], PSOGSA[37], JA [31], MSA[32], (SF-DE) [39] which give respectively : 0.0891p.u, 0.13570 p.u, 0.09700 p.u, 0.09638 p.u, 0.10842 p.u, 0.09454 p.u . It is observed that ESCA gives a better value of Vd with acceptable total cost than these previous methods. Fig.2. Diagram of voltage magnitudes of Type 1 and Type 2 of ESCA algorithm. C. Type 3: Cost with Voltage Stability We added the voltage stability index to the simple quadratic cost function for increasing the performance of the system, which is considered in this case (such as in equation 16). After the application of ESCA we obtain the optimal values of control variables as given in type 3 of Table 2. Thus, the maximum voltage stability index Lmax is reduced by ESCA from 0.1267 to 0.1224 and the cost increases to 800.4102 $/h, also Vd increases to 0.9774p.u. All inequality constraints are respected, the most important is the voltage limits which are represented by good value of voltage deviation Vd It is observed that ESCA gives the best solution than other methods cited in references such as ABC[21], DSA[23], PSOGSA[37], JA[31], MSA[32], SF-DE[39] which give respectively 0.13790 p.u , 0.12499 p.u , 0.12393 p.u , 0.12430 p.u , 0.13713p.u, 0.13745 p.u. The comparison of different results shows that ESCA method improves greatly the solution with the good total cost with minimum Lmax. Table 3. Comparison results of different methods for type 1 and 2 Methods Type n°1 Type n°2 cost Vd cost Vd PSO [11] 800.41 0.8765 806.38 0.0891 ABC[21] 800.660 / / / DSA [23] 800.3887 / 805.261 0.1357 6GWO[30] 801.410 / 803.631 0.0970 PSOGSA[37] 800.4985 0.91373 804.431 0.0963 JA[31] 800.4794 / / / MSA[32] 800.5099 0.9035 803.312 0.1084 SF-DE [39] 800.4131 0.9209 803.719 0.0945 SCA[41] 800.1020 2.0825 843.604 0.1082 MSCA[41] 799.3100 1.4246 849.281 0.1030 ESCA 800.2198 0.9454 804.99 0.0916 Table 4. Comparison results of different methods for type 3 and 4 Methods Type n °3 Type n°4 cost Lmax Ploss Vd PSO [11] / / / ABC[21] 801.6650 0.13790 3.10780 / DSA [23] 800.9331 0.12499 3.09450 / َ6GWO[30] / / 3.41 / PSOGSA[37] 801.2292 0.12393 / / JA[31] 840.7181 0.12430 3.1035 / MSA[32] 801.2248 0.13713 3.1005 0.88868 SF-DE [39] 800.4203 0.13745 3.0844 0.90359 SCA[41] / / 2.9425 1.8161 MSCA[41] / / 2.9334 1.5987 ESCA 800.4108 0.1224 3.0212 1.1317 D. Type 5: Real power losses minimization The minimization of real power losses is treated in this case like as in equation (10) and total function (20). Real power losses are reduced by ESCA to 3.0212 MW with Vd of 1.1317 p.u, see table 5 type 4. It is clear that the total active power losses are greatly reduced from the initial value of the load flow base case which is 5.81 MW. For the comparison with other methods listed in references, the ABC[21], DSA[23] , GWO[30], JA[31], MSA[32], and SF-DE[39] give 3.1078 MW, 3.0945, MW 3.41 MW, 3.1035 MW, 3.1005 MW, 3.0844 MW, respectively. SCA[41] and MSCA[41] give 2.9425 MW and 2.9434 MW but it is an infeasible solution represented by the high value of Vd which caused by most violations in voltage amplitudes limits of PQ buses. It is observed that ESCA gives a good minimum of active power losses with acceptable Vd than the other methods. E. Type 5: Multi fuel Cost Model For this type of non-convex function, the cost takes multiple quadratic forms in each range of real generators power according to the equation given by (8). This model of the cost function is introduced in the generators buses n°1 and n°2 and represented by piecewise quadratic functions which the cost coefficients are given in [11]. In this type, the results of the ESCA is given in Table 5 type 5, the cost obtained by ESCA is 646.4095 $/hr, with Vd of 0.9645 p.u, therefore SCA[41] and MSCA[41] give 648.1366 $/hr and 646.3600$/hr respectively. For this type of function, ESCA gives a better result compared to the SCA method and almost the same result as the MSCA method. Also, all limits on control and state variables are respected. For proving the speed convergence of the ESCA method of a non-convex cost function, the characteristic of convergence is illustrated in figure 3. We observe that ESCA with new parameters converges fast with high robustness and stability to the best value than SCA. From the results it can be concluded that ESCA is able to solve the optimization problems with non convex function with high convergence stability. Table 5. Simulation results with ESCA of types 4,5 and 6. Control variables Type 4 Type5 Type6 Pg1(MW) 51.4212 139.9998 196.9976 Pg2(MW) 80.000 54.9994 52.057 Pg5(MW) 50.000 24.2163 15 Pg8(MW) 35.000 35.0000 10 Pg11(MW) 30.000 19.7111 10 Pg13(MW) 40.000 16.1524 12 V1(pu) 1.0768 1.0874 1.0389 V2(pu) 1.0723 1.0719 1.0152 V5(pu) 1.0527 1.0432 0.95 V8(pu) 1.0586 1.0516 1.0256 V11(pu) 1.0634 1.1 1.0518 V13(pu) 1.0627 1.0495 1.0534 T4,12 0.9967 0.982 1.1000 T6,9 1.0823 1.1 1.1000 T6,10 0.9000 0.9 1.1000 T28,27 0.9838 0.9851 1.0021 Q10 (pu) 0.0500 0.05 0.0500 Q12(pu) 0.0500 0.05 0.0500 Q15(pu) 0.0500 0.05 0.0000 Q17(pu) 0.0500 0.00 0.0000 Q20(pu) 0.0500 0.05 0.0500 Q21(pu) 0.0500 0.05 0.0500 Q23(pu) 0.0295 0.00 0.0500 Q24(pu) 0.0500 0.00 0.0500 Q29(pu) 0.0226 0.05 0.0000 Cost ($/h) 967.6184 646.4095 930.9864 Active Losses 3.0212 6.6790 12.6546 (MW) Vd(pu) 1.1317 0.9645 0.70831 Lmax 0.1271 0.1266 0.1188 Fig.3. Convergence characteristics of SCA and ESCA algorithms of Type 5 Compared to the improved colliding bodies optimization algorithm (ICBO)[27], MSA[32], SF-DE [39],SCA[41], MSCA[41] which give respectively: 645.1668 $/h646.8364$/h, 646.4390$/h, 648.1366$/h and 646.3600 $/h, it is observed that ESCA method gives a good minimum cost with feasible solution of voltage constraints. Really ICBO[27] gives the better solution but is not a feasible solution represented by the high value of Vd which is 1.8232 p.u caused by the violation of voltage limits. F. Type 6: Production Cost Functions with Admission Valve Effects The effect of valves is added to generator buses No. 1 and No. 2; the coefficients of the cost are given in [11]. Thus the expression of the cost was given by the equation (9), and introduction in the global form such in equation (20). Also, the minimum cost obtained by ESCA is 930.9864 $ /h, with 0.7083 p.u. of Vd as given in table 5 type 6. But SCA with old parameters gives 935.699$/h with Vd as 0.9589 p.u. Obviously that ESCA gives a better solution than SCA with best Vd to restrict the violations in voltage limit constraints. It is obvious that ESCA converges fast to the better solution than SCA. The characteristic of convergence is illustrated in figure 4 and show the fast convergence to the global solution of non smooth function type. Table 6. Comparison results of different methods Methods Case n°5 Case n°6 cost Vd cost Vd ABC[21] / / 931.7450 0.4575 ICBO[27] 645.1668 1.8232 / / MSA[32] 646.8364 0.84479 930.7441 0.44929 SF-DE [39] 646.4390 0.93062 / / SCA[41] 648.1366 0.30790 / / MSCA[41] 646.3600 0.93830 / / ESCA 646.4095 0.9645 930.9864 0.70831 Fig.4. Convergence characteristics of SCA and ESCA algorithms of Type 6 Compared with results of other recent meta-heuristic methods such as ABC[21], MSA[32] which give respectively 931.7450 $/h and 930.7441 $/h. The ESCA gives a good global minimum in this case when the objective function is non-smooth and non-convex. The results of different methods are summarized in table 6; we see that the method of SCA with modified parameters greatly improves the results compared to standard SCA with old parameters and other metaheuristic methods of non- convex and non-smooth cost model. The modification of setting parameters of the standard sine cosine algorithm for solving the OPF problem has been suggested in this work. It is based on the best choice of parameters in standard SCA. The SCA algorithm utilizes a simple formulation containing sine and cosine function and easy to implement with a simple adjustment of control parameters. The efficiency of this algorithm appears in the acceleration of the convergence to the best optimum solution with respecting of all constraints and provides a good and acceptable solution. The optimization of several fitness functions such as total fuel cost, fuel cost with voltage profile improvement, the cost with voltage profile enhancement and real power losses of the standard IEEE30 bus may demonstrate the successful application of the ESCA algorithm. Also, the cost with multiple fuel and admission valves was minimized to demonstrate the ability of ESCA to optimize non-convex and non-smooth cost function. The discussion of results provided by ESCA algorithm and the comparison with standard SCA and the other modern meta-heuristic methods makes this algorithm among the best algorithm with high efficiency and leads to the good optimum with fast and robust convergence and high quality of the solution.III. Sine-Cosine Optimization Method
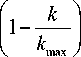
IV. Numerical Results and Discussions
V. Conclusion
Список литературы Optimal Power Flow Solution using Efficient Sine Cosine Optimization Algorithm
- O. Alsac, B. Stott,” Optimal load flow with steady state security”, IEEE Transactions on Power Apparatus and Systems, vol 93 n° 3 pp. 745–751, May 1974.
- Lee K, Park Y, Ortiz J.” A united approach to optimal real and reactive power dispatch” IEEE Transactions on Power Apparatus and Systems, vol. 104 n°5 pp.1147-1153 , May 1985.
- F. Capitanescu,M.Glavic, D.Ernst,L.Wehenkel,"Interior point based algorithms for the solution of optimal power flow problems", Electric Power Systems Research vol. 77 pp. 508-51, April 2007.
- L.L.Lai,J.T.Ma, R. Yokoma, M. Zhao, ”Improved genetic algorithms for optimal power flow under both normal and contingent operation states”, Electrical Power & Energy System, Vol. 19, No. 5, pp. 287-292, June 1997
- A.G.Bakirtzis,P.N.Biskas, “Optimal power flow by enhanced genetic algorithm”, IEEE transactions on power systems”,vol.17,n°2, pp.229-236, May 2002.
- A. Bakirtzis, V. Petridis, and S.kazarlis,”Genetic Algorithm solution to the economic dispatch problem”, Proc.Inst.Elect.Eng., Vol. 141, pp. 377-382, July 1994.
- Sailaja Kumari M, Maheswarapu S. “Enhanced genetic algorithm based computation technique for multi-objective optimal power flow”, Int J Electr Power Energy Syst; vol. 32(6):7 pp. 36–42, July 2010.
- Abdel-Fattah Attia , Yusuf A. Al-Turki and Abdullah M. Abusorrah” Optimal power flow using adapted genetic algorithm with adjusting population size” Elect. Power Compon. Syst., Vol. 40, No. 11, pp. 1285–1299, August 2012.
- Yuryevich J, Wong KP,” Evolutionary programming based optimal power flow algorithm”, IEEE transactions on power systems, Vol.14, No.4, ,pp. 1245-1250, Nov.1999.
- W. Ongsakul, T. Tantimaporn,” Optimal power flow by improved evolutionary programming”, Elect. Power Compon. Syst., Vol. 34, No.1, pp. 79-95, Feb. 2006.
- M.A. Abido. ,”Optimal power flow using particle swarm optimization”, Int J Electr Power Energy Syst.,24 pp.563-571, October 2002.
- Kim JY, Mun KJ, Kim HS, Park JH. “Optimal power system operation using parallel processing system and PSO algorithm”, Int J Electr Power Energy Syst; vol.33(8):14 pp.57–61, October 2011.
- A.A. Abou El Ela, M.A. Abido, S.R. Spea, ”optimal power flow using differential evolution algorithm”,Electric Power Systems Research, vol.80 pp.878–885, July 2010.
- T. Niknam, M. r. Narimani, M. Jabbari, A.R. Malekpour, “A modified shuffle frog leaping algorithm for multi-objective optimal power flow”, Energy, vol.36(11) pp.6420–6432, November 2011.
- Duman S, Güvenç U, Sönmez Y, Yörükeren N. “Optimal power flow using gravitational search algorithm”, Energy Convers Manage, vol.59, pp.86–95, July 2012.
- Bhattacharya A, Roy PK. “Solution of multi-objective optimal power flow using gravitational search algorithm”, IET Gener Transm Distrib; vol. 6(8) pp.751–763, August, 2012.
- Bhattacharya, A.; Chattopadhyay, P.K. “Application of biogeography-based optimization to solve different optimal power flow problems”, IET Gener. Trans. Distrib., vol.5, pp.70–80, Jan. 2011.
- Sivasubramani S, Swarup KS. “Multi-objective harmony search algorithm for optimal power flow problem”, Int J. Electr Power Energy Syst, vol.33(3), pp.745–752, March 2011.
- N. Sinsuphan, U. Leeton, T. Kulworawanichpong, “Optimal power flow solution using improved harmony search method”, Appl. Soft Comput; vol.13(5), pp. 2364–2374, M ay2013.
- Arul R, Ravi G, Velusami S. “Solving optimal power flow problems using chaotic self adaptive differential harmony search algorithm”. Electr Power Compon Syst; vol.41(8), pp.782–805, April 2013.
- M.R. Adaryani, A. Karami, “Artificial bee colony algorithm for solving multi-objective optimal power flow problem”, Int. J. Electr. Power Energy Syst. vol.53 pp.219–230, December 2013.
- H.R. E. Bouchekara& M. A. Abido,” Optimal power flow using differential search algorithm”, Electric Power Components and Systems, vol.42, pp.1683–1699, October 2014.
- K. Abaci , V. Yamacli, “ Differential search algorithm for solving multi-objective optimal power flow problem”, Int J. Electrical Power and Energy Systems, vol.79,pp.1-10, July 2016.
- H.R.E.H. Bouchekara, M.A. Abido, M. Boucherma, “Optimal power flow using teaching-learning-based optimization technique”, Electr. Power Syst. Res. vol. 114 pp.49–59, September 2014.
- P.K. Roy, C. Paul, “Optimal power flow using krill herd algorithm”, Int. Trans. Electr. Energy Syst., vol.25(8) pp.1397–1419, August 2015.
- H.R. El-Hana Bouchekara, M.A. Abido, A.E. Chaib, “Optimal power flow using an improved electromagnetism-like mechanism method”, Electr. Power Compon. Syst. vol. 44 pp. 434-449, 2016.
- H.R.E.H. Bouchekara, A.E. Chaib, M.A. Abido, R.A. El-Sehiemy, “Optimal power flow using an improved colliding bodies optimization algorithm”, Appl. Soft Comput. vol.42, pp.119–131, May 2016.
- Bouchekara HR. “Optimal power flow using black-hole-based optimization approach”,Appl Soft Comput; vol.24, pp.879–888,2014.
- M. Younes, F. Khodja, R. L.Kherfane,” Multi-objective economic emission dispatch solution using hybrid FFA (firefly algorithm) and considering wind power penetration”, Energy vol.67, pp.595-606, April 2014.
- Attia A. El-Fergany & Hany M. Hasanien;” Single and multi-objective optimal power flow using grey wolf optimizer and differential evolution algorithms,” Electric Power Components and Systems, vol.43(13),pp.1548–1559, July 2015.
- W. Warid, H. Hizam, N. Mariun and N. I. Abdul-Wahab,”Optimal power flow using the jaya algorithm”, Energies, vol.9, pp.678-696, August 2016.
- A. A. Mohamed, , Y. S. Mohamed, A. A.M. El-Gaafary.,A. M. Hemeida “Optimal power flow using moth swarm algorithm”, Electric Power Systems Research vol.142,pp. 190–206, January 2017.
- C .Shilaja, K . Ravi, “Multi-objective optimal power flow problem using enhanced flower pollination algorithm”; Gazi University Journal of Science, vol.30(1),pp.79-91, January 2017.
- A. Bhattacharya & P. K. Chattopadhyay,” Solution of economic power dispatch problems using oppositional biogeography-based optimization”, Electric Power Components and Systems, vol.38, pp. 1139–1160, July 2010.
- P.K. Roy, D. Mandal, “Quasi-oppositional biogeography-based optimization for multi-objective optimal power flow”. Electr Power Compon Syst, vol.40, pp. 236–256, December 2011.
- W. Warid, H. Hizam, N. Mariun, N. I. Abdul Wahab,”, A novel quasi-oppositional modified Jaya algorithm for multi-objective optimal power flow solution”, Applied Soft Computing , vol. 65, pp. 360–373, April 2018.
- J. Radosavljevic, D. Klimenta, M. Jevtic, N. Arsic, “Optimal power flow using a hybrid optimization algorithm of particle swarm optimization and gravitational search algorithm”, Electr. Power Compon. Syst. vol.43 (17),pp. 1958-1970, August 2015.
- S. S. Reddy” Optimal power flow using hybrid differential evolution and harmony search algorithm”,International Journal of Machine Learning and Cybernetics. vol.10, pp 1077–1091, May 2019.
- P. P. Biswas, P.N. Suganthan , R. Mallipeddi , G. A.J. Amaratunga,” Optimal power flow solutions using differential evolution algorithm integrated with effective constraint handling techniques” Engineering Applications of Artificial Intelligence, vol.68 pp. 81–100, February 2018.
- Seyed ali Mirjalili, “SCA: A sine cosine Algorithm for solving optimization problems”; Knowledge-Based Systems , Vol. 96 , pp.120-133, March 2016.
- Abdel-Fattah Attia, R. A. El Sehiemy, H. M. Hasanien,” Optimal power flow solution in power systems using a novel Sine-Cosine algorithm”, Electrical Power and Energy Systems vol. 99 pp.331–343, July 2018.


