Optimal Reliable Routing Path Selection in MANET through Novel Approach in GA
Автор: Krishna S.R.M., Seeta Ramanath M.N., Kamakshi Prasad V.
Журнал: International Journal of Intelligent Systems and Applications(IJISA) @ijisa
Статья в выпуске: 2, 2017 года.
Бесплатный доступ
In MANETs (Mobile Adhoc Network) judgment in optimal reliable routing path between source and destination is a challenging task because of the mobility nature of nodes and is deficient in the infrastructure of the network which is so dynamic. So the objective of this paper is to identify an optimal reliable ordered routing paths between source and destination nodes in MANET.To meet the above challenging task the paper focus on an new novel approach in Genetic Algorithm called Parametric fitness based Genetic Algorithm.Proposed algorithm hybridized with classification model rough sets as one key sub component which offers better accuracy results.
Classification, GA, Roughsets, optimality, Performance
Короткий адрес: https://sciup.org/15010901
IDR: 15010901
Текст научной статьи Optimal Reliable Routing Path Selection in MANET through Novel Approach in GA
Published Online February 2017 in MECS
MANET [4][14](Mobile Ad-hoc NETwork) is a network consists of mobile nodes connected by wireless links, using various protocols the path between source and destination mobile nodes is established and data transmission takes place through the routing path. Data transmission in MANET is a complex task because of its features, like infrastructure-less, self-configuring, selfhealing [4] and autonomous system of mobile nodes. Mobile nodes in MANET behave as they wish to avail in the network or not.Before data transmission takes place always achallengingtaskfor nodes is that to identify an optimal reliablepath between source and destination nodes in minimum time.Eventhough various existing models like GA[16-18],ACO[11-13][21] models are there but are limited with time complexity and no reliability.So to find optimal reliable routing paths an novel pproach in GA[21]proposed. In MANETS dynamically routing is done using various routing protocols[6-10].Routing [4][5] is a mechanism to find the best path from the source node to destination node using various standards and rules.
Routing protocols should follow the rules and exhibit routing mechanism well. Mainly four kinds of ad-hoc routing protocols [4] are used for routing in MANETS.
-
II. Optimized Model
Optimized models play an important role in determining routing paths for efficient data communication in wire less network. These existed routing model described in the following sections.
-
A. Genetic Algorithm
The Genetic Algorithm (GA)is a method of machine learning to solve optimization problems. Basically GAconsists of two processes for generating the next generation. The selection of individuals for the production is involved in the first process. And applying crossover and mutation techniques to do manipulation of those selected individuals to get the next generation is in the second process.
GA is based on a single logical figure is called as fitness function (FF) also called as objective function [16]. The fitness function is the value of measurement to get the next generation or the required objective. Chromosome (Genotype) [17] is defined as a set of parameters that specifies a possible solution of the problem which GA vexing to solve. In MANETS chromosome is taken as a sequence of IDs of the nodes in the routing paths.We should improve the fitness value of the chromosome through GA processes[25-30]. The collection of all chromosomes is called as the population or set of chromosomes. In the selection process selective reproduction [18]is applied to the current population, then we select the chromosomes having similar fitness values and better chromosomes will be selected from the parent population. After GA, using crossover and/or mutation operations reproduces new children when acceptable solution generated. Crossover is an operator to generate new chromosome over two parent chromosomes by exchanging strings. A mutation [21] is the process of changing chromosome by exchanging strings on a single chromosome.
-
B. Roughsets
-
2. Battery power (C2): The capacity of the power of a node to do any operation in the network is known as battery power of a node in the network at any instant of time. Initially, consider the total power of a node is 1. Battery energy of a node is calculated with the below formula
с 2=1- ( s+f+r+d )
-
3. Signal strength (C3): The energy of a node to access their neighbor nodes to data transfer is called as the signal strength of the node. The signal strength of a node is calculated as
Rough set Theory (RST) [22] used to deal with uncertain data. It does need any preliminary data, but requires classification rules to simplify knowledge.
Pawlak rough set theory definitions:
Definition1. An info system I,is well-defined as a parameter setI= {U, A}, where U is a nonempty finite set of objects, A is a non-empty finite set of attributes. WhereasCdenotes the set of condition attributes and Ddenotes the set of decision attributes, C∩D= ∅ . Every attribute a ∈ Ais associated with a set Vaof its value, called the domain ofa.
where s is send, f is forward, r is received, d is dropped packets through the node and t is the total number of packets transmitted in the network.
( count ( ND ) ( TP ))
(TN + sum (TT))
-
III. Process Model
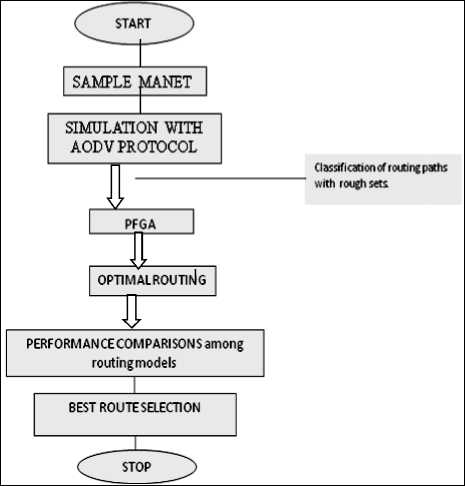
Fig.1. Diagram of processing work
-
A. Performance Metrics
-
4. Mobility (C4): The mobile node moving area with respect to around nodes in a particular interval of time is known as mobility of a node.
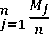
=∑
The five performance metrics involved in this paper are:
1. Number of Hops (C1): Number of hops or edgesinvolved in the path from the source to the destination. Hop or edge is defined as a link between two nodes.
Consider a path 1->2->3->4->5.
Here source node is 1 and destination node is 5 then C1is 4.
|( AVGj ( t ) -AVGj ( t+ Δ t ))|
ST
Dist ( Tlx , ny ) = dista nce between nodes x,y, √( x2- Xl )2-(У2 - У1 )2 , n: no. of nodes, avgx (t) : average distance between node x and all other nodes attime t, ST: simulation time, AVGt: Time period used in computation.
-
5. Trustworthy (C5):Trustworthy of a node can be defined as the amount of trust to accept data transfer along the node that is the node can’t drop more packets.
c 5=T(RREQ) ×Qr+T(RREP) ×Qp+T(DATA) ×
×Qd (4)
where Qr = count of successful request messages with failure messages, Qp = count of successful reply messages with failure messages, Qd = count of successful data packets with failure packets .
T(*) = time value of the node. Here * represents RREP, RREQ, DATA.
Q∗= ( Q ∗ S-Q ∗ ! )
(Q∗s + Q∗f)
Table 1. Manet Instance Data For Evaluation
|
Nodes |
Battery power |
Signal strength |
Trust worthy |
NH |
|
1 |
0.65 |
0.45 |
0.81 |
3 |
|
2 |
0.72 |
0.82 |
0.95 |
4 |
|
3 |
0.32 |
0.34 |
0.45 |
7 |
|
4 |
0.83 |
0.80 |
0.87 |
2 |
|
5 |
0.65 |
0.83 |
0.72 |
4 |
|
6 |
0.47 |
0.67 |
0.65 |
4 |
|
7 |
0.64 |
0.71 |
0.55 |
6 |
|
8 |
0.91 |
0.83 |
0.65 |
7 |
|
9 |
0.81 |
0.59 |
0.47 |
5 |
|
10 |
0.87 |
0.46 |
0.53 |
3 |
|
11 |
0.60 |
0.66 |
0.80 |
5 |
|
12 |
0.57 |
0.57 |
0.67 |
4 |
|
13 |
0.48 |
0.35 |
0.77 |
5 |
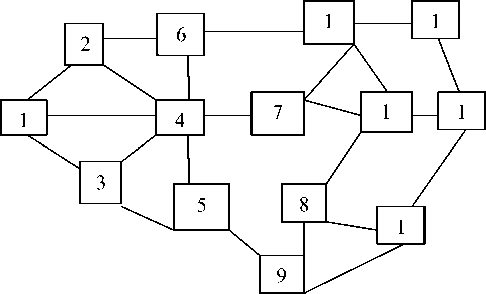
Fig.2. Network diagram for MANET
From the MANET network trace file, calculated performance metric values are given in Table 2, which shows some nodes and its performance metric values of C2,C3,C4 and C5. C1 is calculated from the path scenario. To filter the optimal possible routes from the Network done by the application of rough sets with the following classification rules like:
-
(a) Average Trustworthiness of the path should be > 50%.
-
(b) The average battery power of the path should be > 70%
-
(c) Average Signal Strength should be > 45%
-
(d) Average Number of hops should be <= 4.
After evaluating upper and lower boundary values of the possible routing paths sets with the above classification rules The final filtered routed nodes indicated in BOLD format.
Table 2 shows all paths obtained from the simulatedMANET with AODV protocol.
Table 2. All Possible Routes From Node Source Node 1toDestination
Node 12.
|
Route |
Node Numbers in Routing path |
|||||||
|
R1 |
1 |
2 |
6 |
11 |
12 |
|||
|
R2 |
1 |
3 |
4 |
6 |
11 |
12 |
||
|
R3 |
1 |
4 |
7 |
11 |
12 |
|||
|
R4 |
1 |
3 |
4 |
8 |
12 |
|||
|
R5 |
1 |
3 |
5 |
9 |
8 |
12 |
||
|
R6 |
1 |
3 |
5 |
9 |
8 |
10 |
13 |
12 |
|
R7 |
1 |
3 |
5 |
4 |
8 |
12 |
||
|
R8 |
1 |
2 |
4 |
8 |
10 |
12 |
||
|
R9 |
1 |
2 |
4 |
3 |
5 |
9 |
12 |
|
|
R10 |
1 |
3 |
5 |
9 |
10 |
12 |
||
|
R11 |
1 |
2 |
6 |
11 |
10 |
13 |
12 |
|
|
R12 |
1 |
2 |
4 |
7 |
11 |
10 |
13 |
12 |
|
R13 |
1 |
2 |
4 |
3 |
5 |
9 |
8 |
12 |
|
R14 |
1 |
3 |
5 |
4 |
7 |
12 |
||
|
R15 |
1 |
4 |
7 |
11 |
12 |
|||
|
R16 |
1 |
4 |
7 |
12 |
||||
|
R17 |
1 |
2 |
3 |
4 |
7 |
12 |
||
|
R18 |
1 |
2 |
3 |
4 |
7 |
11 |
12 |
|
|
R19 |
1 |
2 |
3 |
5 |
4 |
7 |
11 |
12 |
|
R20 |
1 |
3 |
4 |
7 |
12 |
|||
-
B. Parametric Fitness Based GeneticAlgorithm (Pfga)
The k, w and C are the constants used in both PFGA and PACO algorithms. PT is the name for paths to be taken as input to the PFGA algorithm. SELECTION(P) is a method to select any two paths for producing the next generation of paths. PDR, NO, AD and PD are the performance metrics calculated from ns2 trace file. CROSSOVER(P), MUTATION (P) are two procedures to apply changes on paths to get new paths. FF is the fitness function should be evaluated for each path. Delete(P) is the function used to remove the path from memory. Finally,the highest FF value having path will be generated by PFGA algorithm.
INPUT: An instance of a model (PT)
Initialize the k, w and C.
while condition doesn’t fail do
SELECTION(P)
FF(x) = y- kx [NO + AD + PD] + Ew , xC , (5)
NN = CROSSOVER(P)
NN = MUTATION (P)
If condition for NN node is existed in network topology then
FF(x) = ^ - k x [NO + AD + PD] + £ wt x Ct else
Delete (P)
end if end while max<- FF(x)
while condition for FF(x)do if max end if end while OUTPUT: Optimal path which has highest fitness value. IV. Results To Generate various routing paths from the sample dynamic network various Parameters set from the SimulatorEnvironment are described in following Table 3. All Simulator results are extracted from NS2[15]trace file. Adhoc On demand routing vector(AODV) Protocol is used for basic simulation. Table 3. Simulation parameters description Parameter Description Parameter Value Number of nodes 25 Data packet size 1000 bytes Environment area 1800X 840 Transmission Range 250m Traffic Type CBR Routing protocols AODV Time Delay 0.0347 ms Parameters Observed Packet delivery ratio, Normalized overhead, End-to-end Delay, Throughput and Number of Packets Drop,Mobility,Signal Strength,Number of hops, Trust Worthy of each node in a Network. Table 4 describes the results that on particular individual nodes number of data packets sent(S) and receive(R) and total delay time period.These results determines the maliscious or non maliscious nature of nodes when the routing path selection takes place under the consideration of 5 metric values battery power,signal strength,number of hops,trust worthy and mobility. Table 4. Performance metrics results for various iterative routing paths Node Number Data Packet Delay S R 1 510 596 65437.5 2 35265 35269 801185 8 1059 1150 148521 13 22260 22357 706795 15 330 35276 811628 20 501 588 63875.6 In the table 5, AM - Average mobility, ASS - Average Signal strength, TNH -Total Number of hops, ATW -Average Trustworthy, ABP - Average Battery power. The table 5, gives the parametric input values of the sample routing paths generated from PFGA Model.Results concludes that models predicts that path 215-19-23 is reliablebecause the path results maximum average Battery Energy, Minimal Mobility and maximum Trust Worthiness. From the trace file analysis Table 6 and Table 7 results the various performance metric parameter values for the best routing path.The results concludes that in both models alternative 2-15-19-23 PFGA offers high throughput, and high trust worthiness which concludes that, the above path is both reliable and optimal routing alternative path in MANET. Table 5. Comparison of Performance Metric Results for best alternative for proposed models (2-15-19-23) among GA and PFGA S.no Path scenario AM TNH ASS ATW ABP 1 2-5-6-23 0.27 21 0.23 0.447 1.71 2 2-8-14-23 0.16 17 0.12 0.734 0.74 3 2-15-19-23 0.12 11 0.87 0.876 1.79 4 2-4-8-23 0.20 19 0.54 0.487 1.74 5 2-3-7-23 0.15 21 0.66 0.823 1.24 1 2-5-6-23 0.27 21 0.23 0.447 1.71 2 2-8-14-23 0.16 17 0.12 0.734 0.74 3 2-15-19-23 0.12 11 0.87 0.876 1.79 4 2-4-8-23 0.20 19 0.54 0.487 1.74 Table 6. Comparison of Performance Metric Results for best alternative for proposed models (2-15-19-23 ) among GA and PFGA . Performance Criterion PFGA Model GA Model NPD 137 264 PDR 1.014 0.002 TP 0.283 0.982 TW 0.265 0.016 END-to-END 0.677 0.312 In the table 6, PDR - Packet delivery ratio, TW - Trust Worthiness, End-to-End - End-to-End Delay, TP – Throughput, NPD - Number of Packets Drop. From the trace file analysisTable 6 and Table 7 results the various performance metric parameter values for the best routing path.The results concludes that in both models alternative 2-15-19-23 PFGA offers high throughput, andhigh trust worthiness which concludes that, the above path is both reliable and optimal routing alternative path inMANET. Table 7 Performance metrics results for various iterative routing paths for the fitness function with variation of k using PFGA Algorithm. S.No Path Scenario Fitness value K=0.09 K= 0.25 1 2-8-14-23 158.457 54.391 2 2-15-19-23 167.507 57.236 Fig.3. Performance time comparison of GA with PFGA Figure 3 gives the observed and computed CPU Consumption or Execution time to generate first 5,10,15,and 20alternatives or routing paths when network size is increased by ‘n’ nodes.The GA results are compared with novel optimized model PFGA.From this Figure 3 series observed that CPU Execution time for PFGA Model decreases by around 40%, 45%, 55%, 50% and 70% on what GA Consumption timefor 10,20,30,40 and 50 nodes ofan Simulated Network.And due to selection of routing paths is simply based on performance metrics, the final optimal routing paths also extracted with high reliability.But where as in GA the generation of optimal routing paths are bounded by distance and no gaurentee in reliability of resulatant optimal paths. V. Conclusion In this Paper we presented an optimization modelto predict optimal ordered reliable routing paths for aMobile adhoc Network.This model tested on a adhoc network under varying network size.The new approach in Genetic Algorithm combined with roughsetssignificantly contributes to determine the bestperformance in predicting optimal reliable path with accuracy compared to other optimized models.The results are compared terms of CPU Execution time,with good Average through put,in terms of all performance metrics compared to other models evenwhen the network size increases with other existing models.Even though other existingmodels are there but all the models are limited with unique parameter distance in determining routing paths and there is no priotrity based metric inputs to determine reliable routing paths.But the PFGA model offers good performance in determining optimal paths when the network sizeincreases to randomly.NS2 tool box[5] is used for determining Input Parameters, performance metrics and 4eMka2 or Rose2 for classifying routing paths.Other time and cost analysis are done using C.Determining optimal routing paths with accuracy when the netwok size and number of alternatives or routing paths increasesrapidlyis still an issue that needs to be investigated in the future.The whole work also can be compared or extended with heuristic and meta heuristic models.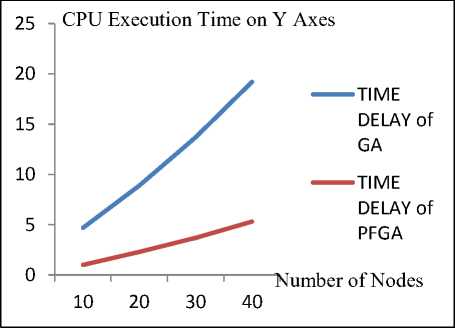
Список литературы Optimal Reliable Routing Path Selection in MANET through Novel Approach in GA
- E.Albayarak and Erensal, Y.C. Using analitic hierarchy process to improve human performance.Journal of Intelligent manufacturing.15.491-503,2006.
- Vinay Kumar Saini , AhP,Fuzzy Sets and TOPSIS Based Reliable Route Selection for MANET.978-93-80544-12-0/14,IEEE Conf,2014 .
- Principles of soft computing by S.N.Sivanandan, S.N.Deepa Second edition, 2012.
- Nadia Qadri, Liotta Antonio, “ A COMPARATIVE ANALYSIS OF ROUTING PROTOCOLS FOR MANETS”,University of Essex,Colchester,UK,IADIS International Conference Wireless Applications and computing 2008.
- T.Henderson ,'The NS-2 Network simulator',software package retrived from http://www.nsnam.org.
- Arun Biradar, Dr. Ravindra C. Thool, Performance Evaluation ofMobile Ad-hoc Networks Routing Protocols to Employ Genetic Algorithm,3rd World Congress on Information and Communication Technologies(WICT 2013), 15-18 December 2013, Hanoi, Vietnam, IEEE.
- Abhishek Roy, Sajal K. Das, "QM2RP : A QoS-BasedMobile Multicast Routing Protocol Using Multi-ObjectiveGenetic Algorithm", Center for Research in Wireless Mobilityand Networking (CRe WMaN),2004.
- Kumar Nikhil, Swati Agarwal and Pankaj Sharma, “application of genetic algorithm in designing a security model for mobile adhoc network”, CSIT, 2012.
- Clarles E. Per Kins and Pravin Bhagwat “Highly Dynamic Destination Sequenced Distance Vector Routing (DSDV) for mobile computer “SIGCOMM, ACM (1994).
- Tarun Varsheney, Aishwary Katiyar, Pankaj Sharma , “ Performance Improvement of MANET under DSR Protocol using Swarm Optimization”, 978-1-4799-2900-9/14, IEEE Conf, 2014
- Arun Biradar, Dr. Ravindra C. Thool, Performance Evaluation ofMobile Ad-hoc Networks Routing Protocols to Employ Genetic Algorithm,3rd World Congress on Information and Communication Technologies (WICT 2013), 15-18 December 2013, Hanoi, Vietnam, IEEE.
- Abhishek Roy, Sajal K. Das, "QM2RP : A QoS-BasedMobile Multicast Routing Protocol Using Multi-ObjectiveGenetic Algorithm", Center for Research in Wireless Mobilityand Networking (CRe WMaN),2004.
- Kumar Nikhil, Swati Agarwal and Pankaj Sharma, “application of genetic algorithm in designing a security model for mobile adhoc network”, CSIT, 2012.
- Clarles E. Per Kins and Pravin Bhagwat “Highly Dynamic Destination Sequenced Distance Vector Routing (DSDV) for mobile computer “SIGCOMM, ACM (1994).
- Aspal Jindal, Vishal Gupta,”Fuzzy Improved Genetic Approach for Route Optimization in MANET”, IJARCSSE, Volume 3, Issue 6, June 20.2013.
- Tarun Varsheney, Aishwary Katiyar, Pankaj Sharma , “ Performance Improvement of MANET under DSR Protocol using Swarm Optimization”, 978-1-4799-2900-9/14, IEEE Conf, 2014.
- AnpingZeng , TianruiLi, DunLiu, JunboZhang and HongmeiChen “ A fuzzy rough set approach for incremental feature selection onhybrid information systems” Science Direct , 2014, 39-60.
- Francisco Rodrigues Lima Junior, Lauro Osiro and Luiz Cesar Ribeiro Carpinetti “A comparison between Fuzzy AHP and Fuzzy TOPSIS methods to supplier selection” Science Direct , 2014, 194-209.
- Annapurna P Patil, Dr K Raj ani kanth, Bathey Sharanya, M P Dinesh Kumar, Malavika J, 'Design of Energy Efficient Routing Protocol for MANET based on AODV', International Journal of Computer Science Issues,Vol. 8, Issue 4, No I, July 2011.
- William Zhu, Student Member, IEEE and Fei-Yue Wang, Fellow, IEEE,’Relationships among Three Types of Covering RoughSets’,IEEE 11--44224444--00113334--X8, 2006.
- T. Jones, S. Forrest, Fitness distance correlation as a measure of problem difficulty for genetic algorithms,in: L.J. Eshelman (Ed.), Proc. 6th Internat. Conf. on Genetic Algorithms, Kaufman, LosAltos, CA, 1995,pp. 184–192
- Y.C. Erensal, T. Oncan, M.L. Demircan, Determining key capabilities in technology management using fuzzy analytic hierarchy process: a case study of Turkey, Information Sciences 176 (18) (2006) 2755–2770.
- D.Y. Chang, Applications of the extent analysis method on fuzzy AHP, European Journal of Operational Research 95 (1996) 649–655.
- F.T. Bozbura, A. Beskese, Prioritization of organizational capital measurement indicators using fuzzy AHP, International Journal of Approximate Reasoning 44 (2) (2007) 124–147.
- O.S. Vaidya, S. Kumar, Analytic hierarchy process: an overview of applications, European Journal of Operational Research 169 (2006) 1– 29.
- D. Merkle, M. Middendorf, Modelling ACO:composed permutation problems, in: M. Dorigo, G. Di Caro, M. Sampels (Eds.), AntAlgorithms, Proc. ANTS 2002, Third Internat Workshop, Lecture Notes in Computer Science, Vol. 2463, Springer, Berlin, Germany, 2002, pp. 149–162.
- M. Dorigo, Optimization, learning and natural algorithms (in Italian), Ph.D. Thesis, Dipartimento di Elettronica, Politecnico di Milano, Italy, 1992.
- M. Dorigo, T. Stutzle, Ant Colony Optimization, MIT Press, Cambridge, MA, 2004.
- T. Jones, S. Forrest, Fitness distance correlation as a measure of problem difficulty for genetic algorithms, in: L.J. Eshelman (Ed.), Proc. 6th Internat. Conf. on Genetic Algorithms, Kaufman, LosAltos, CA, 1995, pp. 184–192.
- D.E. Goldberg, Simple genetic algorithms and the minimal deceptive problem, in: L. Davis (Ed.), Genetic Algorithms and Simulated Annealing, Pitman, London, UK, 1987, pp. 74–88.


