Optimal Reporting Cell Planning with Binary Differential Evolution Algorithm for Location Management Problem

Published Online April 2017 in MECS

The significance of mobile location management in wireless communication has evolved drastically because of tremendous rise in the number of mobile users with the constraint of limited bandwidth. In order to accommodate more subscribers in a wireless network, mobility management accounts as an important factor in designing the infrastructure of the cellular wireless communication network. In a wireless communication, the sphere of mobility management is a complex and intricate challenge with the goal to track the current location of the users so as to route a call or message to the mobile user within the limited resources [1]. The bandwidth is used for the registration of the mobile user as well in searching the user in a network. However, there is a trade-off between location update and location searching (paging) and mobility management tries to balance between these two, so as to minimize the total cost incurred during the mobile location operation.

Location area [2, 3] and reporting cell planning (RCP) [4] are the two main strategies for solving location management problem, however the paper proposes optimal location management using RCP strategy. For solving the complex optimization problems the differential evolution algorithm has been used in various engineering applications and many works are also carried out to enhance the performance of this algorithm by introducing variants or by modifying it [5-7]. Literatures have been reported on nature inspired algorithms for mobility management [8, 9]. A comparison of three artificial intelligence techniques namely Genetic Algorithm (GA), Ant Colony Optimization (ACO) and Tabu Search (TS) for RCP problem has been studied [4]. The location management in mobile networks is efficiently dealt using evolving cellular automata [10]. Recently, the performance of Binary Particle Swarm Optimization (BPSO) algorithm for optimal design of RCP configuration has been reported [11]. The application of Differential Evolution algorithm for cost optimization in location area, reporting cell and realistic networks is proposed in [12-15]. The best parametric values for Differential Evolution algorithm for mobile location management are studied [16, 17] which are taken into consideration in the present work. A combined genetic-neural and Hybrid GA-PSO algorithms reports optimal mobility management [18, 19]. The location management is also addressed using simulated annealing and modified Hopfield approach [20, 21]. A hybrid swarm intelligence approach involving artificial bee colony is proposed for registration area planning problem [22].

With the objective of testing our approaches we have used reference networks and realistic networks using the collected real data from (Bharat Sanchar Nigam Limited) BSNL, Odisha. The research proposes the use of Binary Differential Evolution (BDE) algorithm for solving the important location management problems to find the optimal or near optimal solutions, comparing with the results of the existing works.

The paper organization is as follows. In the section 2 the problem formulation is discussed where the mobile location management is developed as an optimization problem. Section 3 introduces the implementation details of BDE approach for location mobility management. Section 4 provides a number of detailed simulations for reference network configurations as well as realistic networks that shows the applicability of the proposed approach and compared with the results of other authors. Finally, the conclusion and future scope is outlined in section 5.

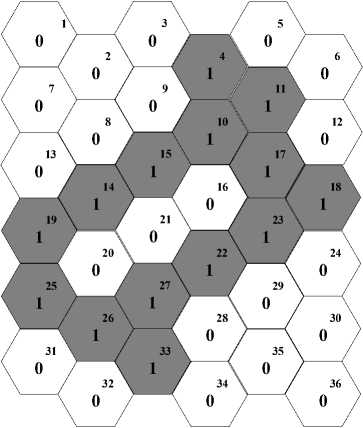
Fig.1. (a) Reporting Cell Planning (RCP) configuration problem

• II.    P roblem F ormulation

The objective of this work is to develop an optimal reporting cell planning (RCP) configuration such that the total location management cost pertaining to location update and paging is minimum. Thus in this section the system model is demonstrated and the cost formulation analysis is presented.

• A.    System Model

The Fig. 1 shows the reporting cell planning (RCP) configuration where the 6x6 cellular networks is divided into reporting cells and non-reporting cells. The reporting cells are given the value 1 (represented in grey color) and non-reporting cells as 0 (represented in white color). The location updating takes place only when a mobile user enters the reporting cell and thus the location update cost involves the sum of the location update weights (frequency of movement into the cell) associated with the reporting cells. In the example shown in Fig. 1(a) there are 14 number of reporting cells out of 36 cells which is a test benchmark RCP configuration [24]. The RCP problem includes determining the optimal number as well as the position of the reporting cells such that the location management cost is minimum.

Fig.1. (b) Vicinity factor values in RCP.

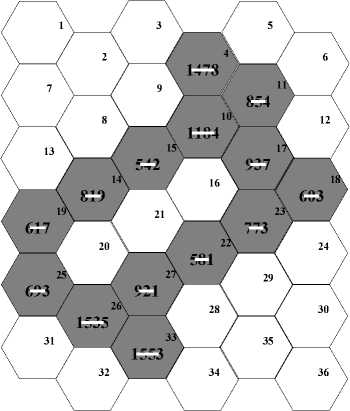
Fig.1. (c) Location updates in RCP problem

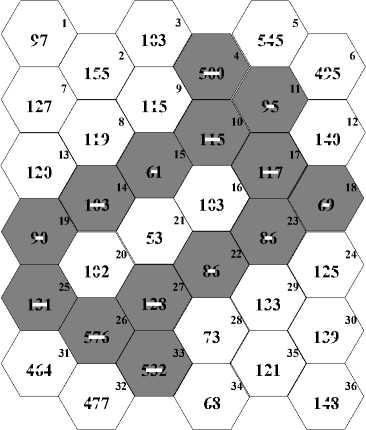
Fig.1. (d) Call arrivals in RCP problem

The tracking of the exact location of the mobile terminal is managed by two operations namely location update (registration) and location inquiry (paging). Location update is done by the mobile terminal to let the network know its current location. Paging is performed by the cellular network to locate the cell in which a mobile user is located so the incoming call for the mobile terminal can be routed to the corresponding base station.

In this paper we have considered the RCP approach in solving the location management issue where the cellular wireless mobile network is divided into reporting cells and non-reporting cells. The reporting cells are those where a location update is performed when a mobile user enters them. So, when a search operation is performed it is restricted only to the last reporting cell as well as its neighbors which are non-reporting cells. The maximum number of cells that are searched (paged) when an incoming call is to be forwarded is termed as vicinity factor. The vicinity factor for a reporting cell is calculated as sum of the number of neighboring nonreporting cells which can be reached without crossing other reporting cells plus the reporting cell itself. Whereas, the vicinity factor corresponding to a nonreporting cell is the maximum vicinity factor among the reporting cells from where this particular cell can be accessed. Fig. 1 (b) presents the vicinity factor values for the reporting cells as well as the non-reporting cells for the given RCP problem. For example, the vicinity factor for cell number 4 which is a reporting cell is calculated by considering the neighbors that are non-reporting cells plus the reporting cell itself(1,2,3,7,8,9,13,5,6,12) which corresponds to the vicinity value of 11. Similarly while calculating the vicinity factor for a non-reporting cell we have to consider the maximum vicinity factor value among the reporting cells from where this cell can be reached. Thus after computing the vicinity values of all the reporting cells the vicinity values of non-reporting cells can be evaluated. For example, the vicinity value of cell number 32 which is a non-reporting cell is calculated by considering the maximum of vicinity factors of reporting cells from where this cell can be reached i.e. cell 25, 26,  33 whose vicinity factors are 6,6,10

respectively. Since the maximum value is 10 it represents the vicinity factor for cell 32.

• B.    Cost Formulation

Location management cost comprises of weighted sum of location update cost and location paging cost given as:

Cost = C x N_{L v} n N_p              (1)

Where N represents the location update cost and N represents the location paging cost over a period of time. The location update cost is generally higher than the location search cost by a factor represented as C which is usually taken as a constant set to 10[11].

Each cell i in the cellular wireless network is associated with two types of weight namely the movement weight ( w ) and the call arrival weight ( w ) where the movement weight represents the number of movements of the mobile terminal into a cell and call arrival weight represents the number of call arrivals within a cell. The location update cost is directly related to the movement weight associated with the reporting cells in a network configuration and given as:

^NLU = ^ w m         (2)

i a R

Where R is the set of reporting cells in the cellular wireless communication network and w represents the movement weight associated with cell i .

The paging cost constitutes the total number of call transactions and is computed as the product of call arrival weight and vicinity factor attributed for that cell and is given as:

N np =£ wjx v(j)            (3)

j = 0

Where N is the total number of cells in a cellular network configuration. The total location mobility management cost is the sum of these two costs i.e. location update cost and location search cost and is given by:

N

Cost = C ^x^ w mi -+ ^ w j X v ( ^j )           ⁽⁴⁾

iaR         j = 0

In order to explain the evaluation of location management cost consider the Fig. 1(c) and (d) where the location update cost and call arrivals are shown corresponding to test data for 6x6 benchmark RCP problem[24]. For this example considering the location update weights presented in Fig. 1(c) the location update cost can be formulated using Eq.(2) NLU=13087

Similarly, the paging cost is evaluated using Eq. (3)

N P = 97X11+155X11+103X11+…….+148X11=65680

Hence, the total cost is determined from the Eq. (4)

Cost=10x13087+65680=198,550

Though the location mobility management cost involves other parameters, they are considered same for all strategies and thus do not affect when comparing the results obtained by several approaches.

The total cost divided by total number of call arrivals gives the cost per call arrival which is given by:

Cost per call arrival = —--- (5)

Z W j j = 0

For the given example Cost per call arrival=198,550/6711=29.58

The cost per call arrival is the objective function which is to be minimized to obtain best cellular wireless communication network configuration. Thus the reporting cell planning problem involves determination of optimal topology calculating the number of reporting cells and their position in a cellular network configuration.

• III.    B inary D ifferential E volution A lgorithm

First proposed by Storn and Price [23] Differential Evolution (DE) belonging to the category of bio-inspired algorithms is a simple, stochastic and effective tool for global numerical optimization. The BDE technique involves four steps namely: initialization, differential mutation, crossover and selection.In this novel BDE algorithm a probability estimation operator is introduced in mutation stage which increases the diversity of the population. On the other hand the standard DE operates in continuous space which is not fit for solving binary coded combinational optimizations. Hence BDE offers an effective way for location cost optimization in RCP which is a discrete binary optimization problem.

• A.    Steps involved in BDE

• 1)    Initialization:

Initialisation step involves the generation of N random potential solutions where N denotes the size of the population.The potential solution (individual) refers to each Reporting cell configuration (RCC) as X i, j where j refers to jth RCC solution. Here X i,j denotes i^th cell ( i^th bit) of j^th RCC solution in the solution set.Thus X_i, j is a binary vector of length equal to the number of cells in the cellular network.

• 2)    Mutation:

After the initialization phase unlike Genetic Algorithm, here differential mutation is performed. Resultant vector namely noisy vector/mutant results using the equation (6):

MV=Xtbest,j +F*(Xrt2,j -Xtr3,j)              (6)

Where X best is the best RCC solution which corresponds to minimum location management cost in the RCC solution set X.X r2 and X r3 are the solutions selected randomly from RCC solution set X. Here DE/best/1/exp variant of DE strategy is used. Scalar factor F controls the amount of variation introduced and its value lies in the range [0, 1].

Probability Estimation Vector (PEV): The PEV is computed using the mutant vector as shown in the Eq. (7):

PEVCXj¹^ — J у    (7)

where b is the bandwidth factor which is a real positive constant generally taken as 20. The range and the shape of the probability distribution model is determined by this factor. The RCC vector which is calculated bit by bit in the binary space and obtained after probability estimation is called probability estimation vector (PEV). The binary mutant RCC individual (BMI) is generated using this PEV using the Eq.(8):

BMIt+1

'1,if rand <  PEV ( X*^ ¹ )

0,        otherwise

• 3)    Crossover:

After crossover, trial RCC solution is created by using the strategy given in Eq. (9):

t+1

^T i,j

BMl j _ X h. j ,

if rand < Cr otherwise

Where C r denotes crossover ratio whose optimal value is 0.15 [20]. The C r value is compared with a generated random number and if it’s greater than the random value then the corresponding element of binary mutant individual is taken to the trial vector. Whereas, the target vector parameters are reciprocated to the trial vector if value of C_r is less than the random number.

• 4)    Selection:

In the selection process based on the suitability (fitness) of the candidate solutions they are passed on to the next generation. If the location management cost of the trial RCC solution obtained after crossover operation is less as compared to that of the target RCC solution, then the trial vector replaces the target vector otherwise the target vector continues in the next generation which is demonstrated in Eq. (10). The X new is the new RCC solution set given as

V t+1   = i,j(new)

T *+¹ ,if Cost( T ^t+1 ) <  Cost(Xt_Id)

^Xr^t 1, j ^,

otherwise

• B.    Implementation flowchart

The binary differential evolution algorithm for RCP problem is discussed briefly:

• 1.    Initially the RCC solutions are generated in random.

• 2.    Setting of control parameters like iteration number, F (scaling factor), b (bandwidth factor) and C r (crossover ratio)is done.

• 3.    The evaluation of fitness of each of the random initial RCC solutions is done using Eq. (5) and the RCC solution whose location management cost is minimum is identified and denoted as X best . Also a target vector X r1 and two random RCC solutions X r2 and X r3 are choosen.

• 4.    Weighted difference vector and mutant/noisy vector is computed followed by probability estimation vector.

• 5.    Using probability estimation vector,binary mutant RCC vectors are generated.

• 6.    The trial RCC vector is evaluated by using parameters from target vector or binary mutant indivisual based on crossover ratio as given in Eq.(9).

• 7.    The selection procedure compares the fitness value

• 8. This process continues from step 3 till the stop condition is satisfied.

of trial vector and target vector and if the cost of trial is less than that of target vector then the target is replaced by the trial and survive to the next generation. In this way a new set of RCC solutions is set for the next generation.

The pseudo code of the BDE algorithm is presented in Table 1 and also illustrated in the flow diagram given in Fig. 2.

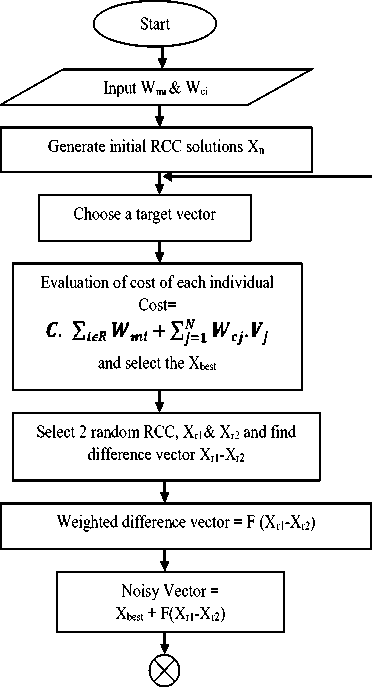
Fig.2. Flowchart implementation of BDE algorithm for RCP problem

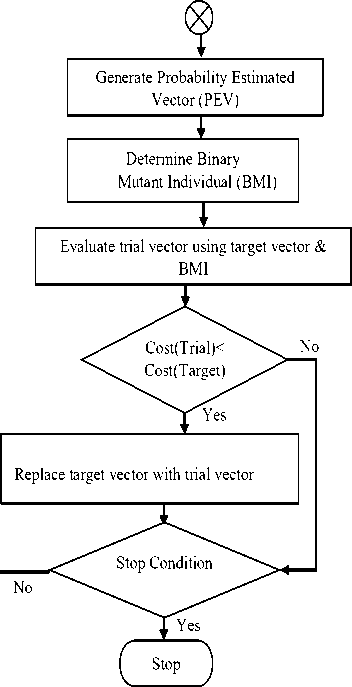
Table 1. Pseudo code of bde algorithm

Steps	Process Involved
1	Population initialization
2	Evaluate cost of each individual solution
3	While(stop condition not satisfied) {
4	Randomly select two vectors Xr1 and Xr2
5	Find difference vector = Xr1-Xr2
6	Weighted difference vector=F. (Xr1-Xr2)
7	Evaluate Noisy vector= Xbest+ F. (Xr1-Xr2)
8	Generate   Probability   Estimation   Vector   using Probability Estimation Operator
9	Determine Binary Mutant Individual (BMI)
10	Evaluate Trial vector by choosing genes from Target vector or BMI
11	Select the target vector or trial vector for next generation population based on lower cost}

• IV.    S imulation R esults and A nalysis

This section presents the simulation results for location management problem through two distinct experiments. First, by using reference data for networks available in literature and second by using realistic networks of BSNL, Odisha. The experimental simulations are conducted taking different networks of size 4x4, 6x6 and 8x8. The optimal parameters that are used for BDE algorithm for solving RCP problem are: Population size= 175, C r = 0.15, F=0.5, b=20 [17]. We DE/best/1/exp variant is used for optimal results. The simulation results are obtained for 250 iterations. Thedetailed comparision is carried out for demonstrating the performance analysis of different state-of-art techniques reported in the literature for solving RCP problem of location management issue.

Experiment 1- Cost analysis using the reference data available in literature

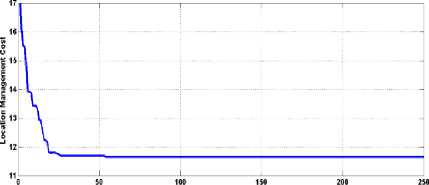
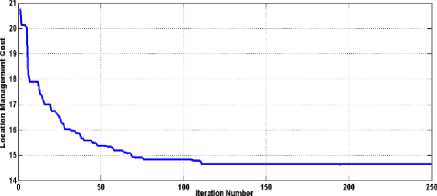
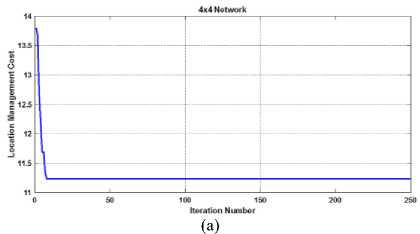
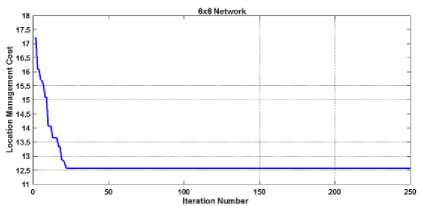
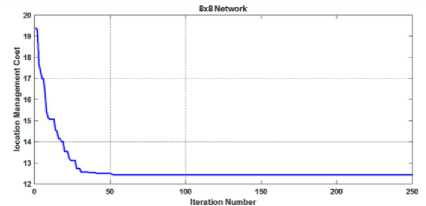
This work presents the simulation analysis taking the weight attributes for reference networks. The weight attributes for call arrival weight and location update weight for 6x6 cells configuration is shown in Table 2 which is available in [4,17]. The column 1 shows the cell number, the column 2 indicates the frequency of location updates in that particular cell and the column 3 corresponds to frequency of arrival of calls. The convergence floor of proposed BDE method for the reference networks of size 4x4, 6x6 and 8x8 is shown in the Fig. 3.

6x6 Network

Iteration Number

(b)

8X8 Network

(c)

Fig.3. Trend of cost function convergence for RCP reference networks of size (a) 4x4, (b) 6x6 and (c)8x8

Experiment 2- Cost analysis using realistic network of BSNL, Odisha

Also the results are validated for realistic network of BSNL,Odisha which shows the applicability of BDE based location management in real scenario.

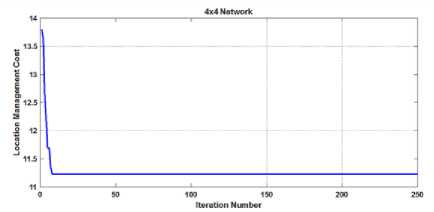
The data sheet for real network with 6x6 attributes is referred in Table 3. A typical run of the proposed BDE approach for cost optimisation in RCP problem taking realistic BSNL, Odisha network is presented in Fig. 4.

Table 2. Weight attributes for reference data network of size 6x6

Cell	NP	NLU	Cell	NP	NLU	Cell	NP	NLU
1	714	1039	13	238	507	25	328	16
2	120	1476	14	964	603	26	255	332
3	414	262	15	789	1479	27	393	1203
4	639	442	16	457	756	28	370	1342
5	419	1052	17	708	695	29	721	814
6	332	1902	18	825	356	30	769	747
7	494	444	19	462	1945	31	17	146
8	810	1103	20	682	1368	32	265	904
9	546	1829	21	241	1850	33	958	359
10	221	296	22	700	1131	34	191	1729
11	856	793	23	23	236	35	551	190
12	652	317	24	827	1622	36	467	1907

Table 3. Weight attributes for bsnl, odisha real network of size 6x6

Cell	NP	NLU	Cell	NP	NLU	Cell	NP	NLU
1	807	349	13	289	38	25	5003	24
2	700	61	14	236	105	26	2621	154
3	398	321	15	451	193	27	1805	149
4	185	21	16	700	480	28	724	406
5	1197	6	17	1164	486	29	1674	865
6	980	30	18	732	865	30	386	297
7	533	285	19	585	171	31	1177	805
8	1556	324	20	435	301	32	601	173
9	163	36	21	1189	514	33	321	120
10	497	289	22	26	9	34	271	426
11	3567	2045	23	3	7	35	1189	1068
12	1917	187	24	8	25	36	535	794

(a)

for Location Management Problem

(b)

(c)

Fig.4. Trend of cost function convergence for realistic BSNL,Odisha networks of size (a)4x4, (b)6x6 and (c) 8x8

Table 4. Cost comparison for different size networks using reference and real networks

Ref. data network	Location update cost	Paging cost	Total cost
6x6	13900	75313	214313
8x8	35260	147357	499957
Real data network	Location update cost	Paging cost	Total Cost
6x6	13900	75313	214313
8x8	33328	125617	458897

Table 5. Call to movement ratio analysis for reference network and real network

Network size (Ref. Network)	Sum of Call Arrival weights(a)	Sum of movement weights(b)	Call to Movement Ratio=(a)/(b)
6x6	18418	33192	0.5548
8x8	31656	64423	0.4913
Network size (Realistic Network)
6x6	12429	34625	0.3589
8x8	44834	98765	0.4539

Table 6. Ratio of reporting cells for best rcp solutions for real data and reference data networks

Network Size	Ratio of Reporting Cells
Service Data(Real Data)
6 x 6	31/36=0.861
8 x 8	55/64=0.859
Network Size	Ratio of Reporting Cells
Service Data(Reference Data)
6 x 6	23/36=0.638
8 x 8	43/64=0.671

Table 7. No. of iterations to attain the convergence