Оптимальная дискретизация скоростной шкалы при измерении мессбауэровских спектров

Непосредственной целью эксперимента в мессбауэровской спектроскопии является регистрация интенсивности гамма-квантов, связанной с процессами резонансного поглощения или рассеяния в определенном диапазоне энергий. Для осуществления процесса сканирования по энергии используется метод доплеровской модуляции энергии испускаемых источником гамма-квантов, которое происходит за счет механического движения источника относительно исследуемого образца в необходимом диапазоне скоростей (как правило, это диапазон скоростей от 0 до ± 30 мм/с).

Закон изменения скорости во времени задается таким образом, чтобы скоростная шкала была линейной ( v = а·t , где а — масштабный множитель). Функция v ( t ) является периодической, т. к. для набора спектра с необходимой статистической достоверностью его регистрация происходит в течении каждого периода с последующим суммированием данных, накопленных в предыдущих периодах (рис. 1).

Экспериментально наблюдаемый мессбауэровский спектр представляет собой зарегестрирован-ную с помощью многоканального накопителя зависимость интенсивности гамма излучения от величины доплеровской скорости, которая в свою очередь зависит от времени. При этом весь диапазон интересующих экспериментатора значений скоростной шкалы [vmin, vmax] делится на участки (каналы): первый канал охватывает значения от vmin до некоторого значения v1; второй канал — от v1 до v2 и т. д. Величина Δj = v(j+1) – v(j) называется шириной j-го канала. В мессбауэровской спектроскопии принято выбирать все ширины каналов одинаковыми. Такой способ дискретизации принято называть дискретизацией по времени с кратными интервалами. В этом случае непрерывная по аргументу функция I(v) преобразуется в функцию I(vj ) дискретного аргумента vj . В данном случае vj означает, что в j-м канале значение аргумента является его средним значением в пределах данного канала.

В связи с этим как перед разработчиками аппаратуры для мессбауэровских исследований, так и перед экспериментатором, использующим эту аппаратуру, возникает вопрос: какое количество каналов многоканального накопителя необходимо, чтобы при изучении и интерпретации экспериментального спектра по совокупности отдельных значений I ( v _j ) получить искомую функцию I ( v ) с наименьшими искажениями. Такая проблема должна решаться на основе априорных сведений о спектральных характеристиках сигнала I ( v ). В подавляющем большинстве случаев функция I ( v ) является суперпозицией набора лоренцевских линий, отражающих зависимость сечения резонансного поглощения или рассеяния в анализируемом образце. На рис. 2 приведен пример экспериментального мессбауэровского спектра, измеренного в геометрии пропускания, где точками обозначено число импульсов в каналах многоканального

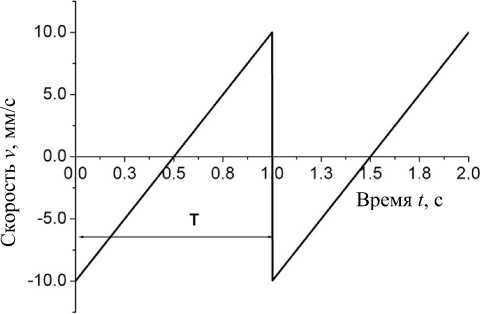
Рис. 1. Закон периодического изменения скорости доплеровского модулятора от времени t . T — период сигнала

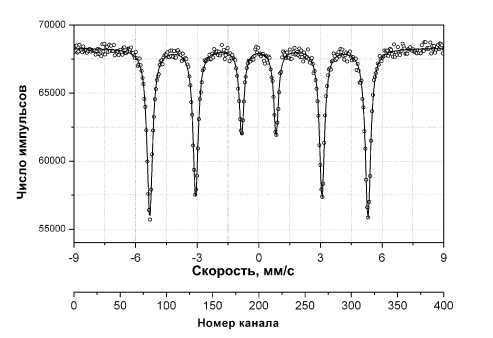
Рис. 2. Экспериментальный мессбауэровский спектр образца металлического железа. Ось абсцисс приведена в двух вариантах: в виде скорости в мм/с и числа каналов.

накопителя, а непрерывная кривая является искомой функцией I ( v ), полученной в результате математической обработки полученных данных.

Наиболее важный вопрос при дискретизации скоростной шкалы — выбор оптимального шага дискретизации Δj. При малых величинах Δj количество каналов j окажется большим, и, следовательно, точность воспроизведения функции I(v) на интервале [vmin, vmax] будет высокой. При этом сократится длительность временнóго интервала, приходящегося на каждый канал, что приведет к уменьшению количества импульсов I(vj ), набранных в каждый канал. Это в свою очередь потребует увеличения времени, необходимого для накопления спектра с необходимой статистической точностью. Под точностью понимается величина, равная отношению амплитуды сигнала к среднему уровню шумов. При больших значениях шага дискретизации Δj количество каналов уменьшается, следовательно, точность воспроизведения I(v) снижается, т. к. происходит сильное усреднение этой функции внутри интервала Δj. Поэтому оптимальной является такая дискретизация, которая обеспечивает представление искомой функции с заданной точностью при минимальном количестве каналов j. В этом случае все отсчеты I(vj ) становятся существенными для восстановления исходной функции. При неоптимальной дискретизации, кроме существенных отсчетов, будут возникать и отсчеты, которые избыточны для восстановления функции с заданной точностью. Ввод избыточной информации в ЭВМ для обработки данных отрицательно скажется и на скорости их обработки. Оптимальный выбор шага дискретиза- ции оценивается по той ошибке, с которой удается воспроизвести искомую функцию I(v).

Существуют разные критерии оценки (выбора) оптимального шага дискретизации. Рассмотрим два возможных подхода: первый подход базируется на спектральном анализе с помощью частотного критерия, второй — на анализе формы спектра при дифференциальном представлении результатов.

ДИСКРЕТИЗАЦИЯ СКОРОСТНОЙ ШКАЛЫ НА ОСНОВЕ ЧАСТОТНОГО КРИТЕРИЯ (ЧК)

Наиболее широкое применение в практике цифровой регистрации и обработки сигналов получил критерий, названный частотным критерием Котельникова, при котором шаг дискретизации выбирают с учетом анализа частотного спектра сигнала.

Рассмотрим возможность применения критерия Котельникова к решению задачи выбора в случае мессбауэровской спектроскопии.

Cущность теоремы Котельникова—Шеннона [1, 2] заключается в том, что если наибольшая частота f m в спектре произвольной непрерывной функции I ( v ) не превышает ½ частоты ее дискретизации, то она без потери точности может быть представлена в виде числовой последовательности значений I ( v _j ) (где j = 0, 1, 2,…), и однозначно восстановлена по этой последовательности. Это означает, что существует такой максимальный интервал Δ (ширина канала), при котором имеется возможность с высокой точностью восстановить искомую функцию I ( v ) по дискретным отсчетам I ( v _j ).

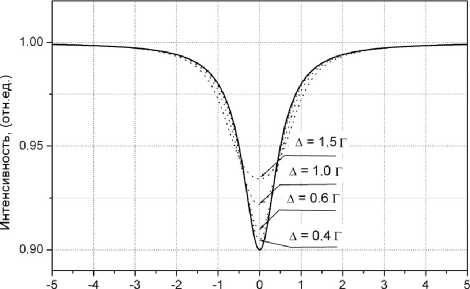
( v /Г)

Рис. 3. Искажение формы спектральной линии в зависимости от ширины канала относительно ширины резонансной линии эталона

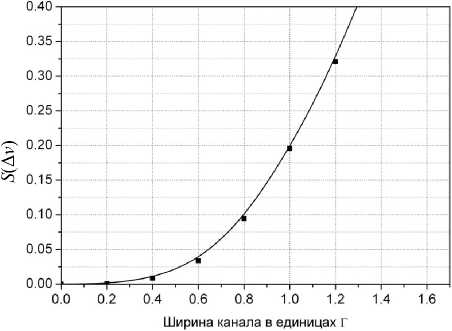
Рис. 4. Зависимость среднеквадратичного отклонения формы спектральной линии от ширины канала, выраженной в единицах ширины резонансной линии эталона

Этот максимальный интервал равен

А =

.

2 • f m

В мессбауэровской спектроскопии на пропускание функция I ( v ) записывается в виде свертки функций источника и поглотителя и называется интегралом пропускания [3]

to

I(v) = C J S(v - vS ) • exP(-ta • ^a (vs )) • dvs , (2) -to где С — константа, v — текущее значение доплеровской скорости; vS — параметр, задаваемый схемой эксперимента; S(v – vS) — приборная функция (функция источника излучения); ta — толщина поглотителя, σa — функция, описывающая отклик поглотителя на монохроматическое излучение.

Форму приборной функции в мессбауэровской спектроскопии принято считать лоренцевской. В большинстве случаев при условии малости t a функция I ( v ) может быть представлена в виде суперпозиции лоренцевских функций:

в формуле (3) минус перед знаком суммы заменяется на плюс.

Так как экспериментальный спектр регистрируется в конечном числе каналов многоканального накопителя, то возникают отклонения формы линии от лоренцевской. В этом случае форма линий будет описываться сверткой двух функций: I ( v ) и ступенчатой функции прямоугольной формы, описывающей ширину канала Δ v многоканального накопителя. Для наглядности рассмотрим влияние ширины канала на искажение формы линии на примере одиночной спектральной линии.

В результате свертки выражение для формы -й линии будет иметь вид [4]:

I ( v ) = -

π

arctg( v +—А v - v , ) -

^arctg⁽ v ^- 2 ^А v ^- v , ) .

I ( v ) = 1 0

-

у A     ( Г /2) 2

£ ⁱ ( v - v , )² + ( Г i /2) 2 ,

где I 0 — интенсивность фона, обусловленная нерезонансными процессами; — номер соответствующей резонансной линии; n — количество резонансных линий; A — амплитуды этих линий; Г — наблюдаемые ширины линий; v — их положения. В случае спектроскопии на рассеяние

На рис. 3 приведен график показывающий влияние ширины канала на форму спектральной линии. За ширину Г спектральной линии будем принимать естественную ширину, которая является минимальной. В дальнейшем спектр с такой шириной линии будем называть эталоном. Для описания формы такой линии необходимо брать минимальную ширину канала Δ. Это условие является наиболее жестким условием, которое накладывается на определение величины Δ.

В качестве критерия отклонения воспроизводимой с шириной канала A v функции I ( v_k, А v ) от исходного сигнала I ( v ) мы применили критерий

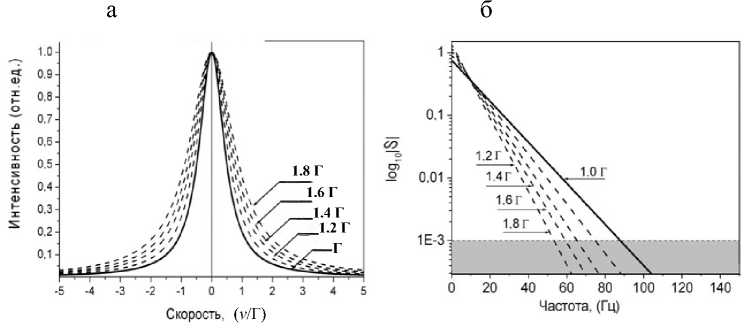
Рис. 5. Сигнал в виде одиночной резонансной линии лоренцевской формы (а) и ее частотный спектр | S | в логарифмическом масштабе (б).

Заштрихованная область указывает на предел по интенсивности, ниже которого отсекаются высокочастотные гармоники

среднеквадратичного отклонения

m

S (Av) = £ k =1

( I ⁽ V ) - I ⁽ v k , ^A V ) ² I ( v )

где k — число точек, в которых рассчитывались значения функций. Зависимость среднеквадратичного отклонения S (∆ v ) от ширины канала приведена на рис. 4.

Из рисунка видно, что отклонение от лоренцев-ской формы становится значительным, когда ширина канала приближается к ширине линии Г. Отклонение проявляется в виде уширения линии и уменьшения ее амплитуды. Такое искажение приводит к снижению верхней границы частотного спектра для резонансных линий с ширинами, большими чем Г, по сравнению с верхней границей частотного спектра исходной линии I ( v ). Теперь можно приступить к установлению верхней границы частотного спектра f_m дискретизируемого сигнала. В соответствии с теоремой Котельникова—Шеннона по формуле (1) можно определить минимальную ширину канала Δ v (шаг дискретизации).

Анализ спектрального состава функции I ( v ), описывающей процесс ядерного резонансного гамма-поглощения, проведем на основе ее прямого фурье-преобразования. Для большей наглядности, не умаляя общности, ограничимся рассмотрением мессбауэровского спектра в виде одиночной спектральной линии ( i = 1) в резонансной части выражения (3). Так как v линейно зависит от t , то выражение для определения частотного спектра будет иметь следующий вид:

v max

• S ( jto ) = J I ( v ) • e - ^{j m v} d v . (6) v max

На рис. 5 приведено семейство функций I ( v ) в виде одиночной резонансной линии различной ширины и их частотные спектры, полученные в результате прямого преобразования Фурье.

Если отбросить гармоники малой относительной величины (в нашем случае менее 0.001 от основной гармоники), то можно определить верхнюю границу частотного спектра f max резонансной линии, которая позволяет оценить верхнюю границу ширины канала Δ max (таблица). Из рис. 5 видно, что f max будет зависеть не только от ширины Γ спектральных линий, но и от задаваемого предела отсечки δ высокочастотных гармоник, входящих в фурье-разложение этих линий. Поэтому для корректного определения Δ max необходимо проводить оценки f max для составляющих спектр резонансных линий с наименьшей шириной. Такими в мессбауэровской спектроскопии являются линии, наблюдаемые для эталонных образцов. Чтобы результат не зависел от конкретного мессбауэровского изотопа, применяемого в эксперименте, будем представлять все результаты в единицах ширины линии Γ, которая зависит от применяемого мессбауэровского изотопа.

Проведенные выше оценки верхней границы частотного спектра относились к случаю, когда не учитывался вклад статистического разброса в значение интенсивности набора. Теперь рассмотрим его влияние на определение верхней границы частотного спектра. С этой целью воспользуемся понятием качества спектра. Под качеством спектра K обычно подразумевают отношение

Расчетные значения ширины канала и необходимого числа каналов для резонансных линий с различными значениями Г при верхних пределах отсечки δ высокочастотных гармоник, равных 0.001 и 0.0001

№ п/п	Ширина резонансной линии в единицах Г	f max , Гц	Максимальная ширина канала Δmax для интервала ± 21 Г	Необходимое число каналов для интервала ± 21 Г
δ = 0.001
1	1.0	88	0.21 Г	196
2	1.2	74	0.28 Г	148
3	1.4	65	0.32 Г	130
4	1.6	59	0.35 Г	118
5	1.8	53	0.39 Г	106
δ = 0.0001
1	1.0	114	0.18 Г	228
2	1.2	88	0.23 Г	178
3	1.4	77	0.27 Г	154
4	1.6	69	0.30 Г	138
5	1.8	62	0.34 Г	124

величины аналитического сигнала к среднему уровню шумов.

В мессбауэровской спектроскопии величина аналитического сигнала непосредственно связана с относительным значением сечения резонансного поглощения ε ( v _j ) , которая в геометрии на пропускание имеет вид

I(∞) - I(vj) ε(v ) =               , j        I(∞)

где I ( ∞ ) — интенсивность прошедшего излучения вдали от резонанса, I ( v _j ) — интенсивность излучения в окрестности резонанса. Если максимум резонанса будет наблюдаться при скорости v _{j 0} , то амплитуда сигнала будет равна А = ( I ( ∞ ) - I ( v _jo ) , а величина шум а в соответствии с законом Пуассона будет I ( ∞ ) . В этом случае выражение для качества спектра будет иметь вид:

A                   ,------

• K = ", ^А   = ε ( v j 0 ) ⋅ JI ( ∞ ).          (8)

I ( ∞ )

Для демонстрации влияния шума на определение f max , а следовательно, и Δ max проведем прямое фурье-преобразование модельных спектров с разной величиной K . Исходные спектры, и результаты их фурье-преобразования приведены на рис. 6.

Из рис. 6 видно, что чем хуже качество спектра, тем ниже верхняя граница частотного спектра и тем большую ширину канала можно задавать. Поэтому, если стоит задача детального исследования формы экспериментального спектра, то необходимо в первую очередь не увеличивать число каналов в нем, а добиваться измерения спектра с более высоким качеством.

В практике оцифровки спектральных данных возможен и другой подход, основанный на представлении экспериментальных результатов в виде дифференциального аппаратурного спектра d ( v ) [5].

ДИСКРЕТИЗАЦИЯ СКОРОСТНОЙ ШКАЛЫ ПРИ ДИФФЕРЕНЦИАЛЬНОМ

ПРЕДСТАВЛЕНИИ СПЕКТРА (ДП)

Как и в предыдущем рассмотрении, весь диапазон интересующих значений v разбивается на участки (каналы). Тогда дифференциальным аппаратурным спектром называется функция

d ( v ) = I ( v j ) /∆ j (9)

где I ( v _j ) — количество зарегистрированных импульсов, удовлетворяющих условию v j ∈ [ v j , v ( j +1) ]. Из (9) следует, что d ( v ) представляет собой кусочно-постоянную функцию (гистограмму). Однако обычно непрерывный набор значений v не используется. Значение d ( v ) приписывается некоторой

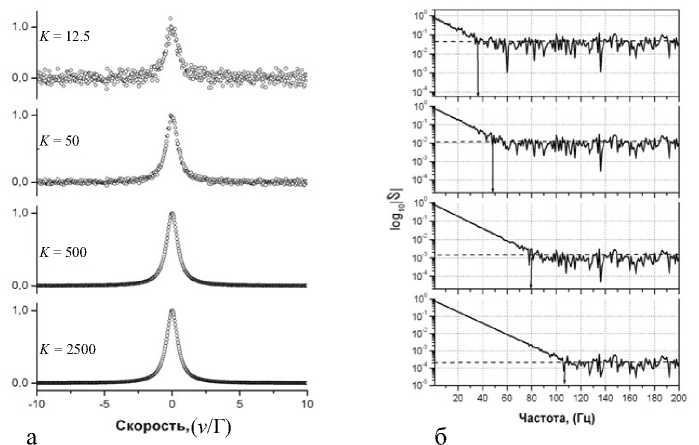
Рис. 6. Резонансная часть модельных спектров с разным параметром качетва K (а). Результаты фурье-преобразования этих же спектров (б)

точке внутри канала, чаще всего его середине. Следует отметить, что дифференциальный аппаратурный спектр в общем случае является случайной функцией. При очень большом статистическом наборе его случайный характер практически не играет роли, поэтому вначале рассмотрим случай большого статистического набора, т. е. когда статистическим разбросом можно пренебречь. Тогда число импульсов, зарегистрированных в данном канале, можно считать равным их среднему значению. Как уже отмечалось выше, если I ( v ) — искомая функция (истинный спектр), то среднее значение будет равно

А /2

d ( v ) =       I ( v + a ) • d a ,          (9)

^А -А /2

где точка v — является серединой канала. Видно, что d ( v ) совпадает с I ( v ) только в том случае, когда ∆ → 0. При конечных значениях ∆ можно говорить, что функция d ( v ) воспроизводит функцию I ( v ) с некоторой погрешностью (погрешность дискретизации). Оценим, как зависит эта погрешность от ширины канала. Будем считать, что в пределах ширины канала функция I ( v ) меняется слабо. Тогда можно разложить подынтегральное выражение в ряд вокруг точки v с точностью до члена второго порядка

I ( v + a ) » I ( v ) + 1\v )a + ^ 1 "( v )a ².    (10)

Подставим это выражение в интеграл (7). Тогда функция d(v) примет вид d (v) = I (v) + 241"(v) •А2.

Второе слагаемое в (11) представляет собой искомую систематическую погрешность σ , обусловленную дискретизацией. Из выражения (11) видно, что ширину канала необходимо выбирать такой, чтобы погрешность σ не превышала заданной величины:

<7 >

—Г( v ) •А ²

Выражение (12) позволяет проводить оценку величины Δ без учета влияния статистического разброса. На рис. 7 приведена зависимость ∆( v ), рассчитанная для спектральной линии эталона. Видно, что минимальная ширина канала будет в том месте на скоростной шкале, где находится максимум функции I ( v ). Это значение на рисунке подчеркнуто жирной линией. В стороне от резонанса ширина канала может быть существенно выше. Однако, как было отмечено ранее, в мессбауэровской спектроскопии все ширины каналов равны друг другу, поэтому минимум функции на рис. 7 определяет минимальную ширину канала для достижения заданной точности.

Приведенное выше рассмотрение выбора ширины канала относилось к случаю, когда можно

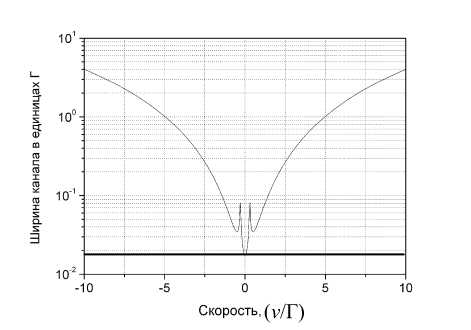
Рис. 7. Зависимость изменения ширины канала от положения резонансной линии на скоростной шкале.

Жирной, горизонтальной линией отмечен уровень, определяющий минимальную ширину канала для σ = 0.001

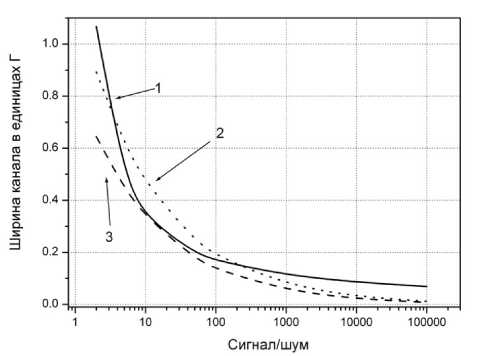
Рис. 8. Зависимости ширины канала Δ от соотношения сигнал/шум K , рассчитаных на основе ЧК (кривая 1) и на основе ДП с коэффициентами запаса β = 2 (кривая 2) и β = 3 (кривая 3)

пренебречь статистическим характером спектра, т. е. когда величина, определяющая качество спектра более 1000.

Величину σ можно задавать и исходя из ее статистического характера. Случайная величина I ( v _j ) распределена по закону Пуассона, следоват ельно , среднеквадратическая погрешность равна I ( v _j ) . Среднеквадратическая погрешность функции d ( v ) во всем интервале изменения j будет равна:

А<

24 2 - 1 ( v )

N [ I Ч V ) ] 2 - в²

Из выражения (15) следует, что ширина канала зависит от формы спектра и значения v , а т. к. в мессбауэровской спектроскопии принято иметь одинаковую ширину канала во всем диапазоне изменения v , то ее следует определять из неравенства

_ V Iv ) _ A d ( V y )

" ' ⁽ v)         \       \    \

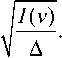
A < min <

v

24 2 - 1 ( v )

При выводе среднеквадратичной погрешности мы пренебрегли вторым слагаемым в выражении (11). Это означает, что ширину канала целесообразно выбирать так, чтобы систематическая погрешность была мала по сравнению со статистической погрешностью и, следовательно, ею можно пренебречь, что важно с практической точки зрения. В этом случае должно быть выполнено следующее неравенство

Iv > ^в I "( v ) -A 2 , A 24

где множитель в = 2 ^ 3 учитывает тот факт, что неравенство должно быть выполнено с запасом. Следовательно, условие для выбора ширины канала будет иметь вид

Таким образом, полученное неравенство можно использовать для определения минимальной ширины канала, необходимой для набора спектров с минимальными искажениями формы линии.

ЗАКЛЮЧЕНИЕ

Предложены два независимых подхода для оптимальной дискретизации мессбауэровских спектров, которые приводят к близким результатам. На рис. 8 приведены графики иллюстрирующие зависимость ширины канала от качества спектра (соотношение сигнал / шум). Графики рассчитаны как на основе частотного критерия (ЧК), так и на основе дифференциального представления.

Из графика видно, что для обеих моделей наблюдается сильная зависимость ширины канала

от качества спектра (соотношения сигнал / шум). Например, если ширина канала Δ, составляет 0.2 от ширины линии эталона Г, соотношение сигнал / шум должно находится в диапазоне 50–100, в то время как при выборе Δ = 0. 1 Г это соотношение должно быть уже не менее 10 000.

Если величина эффекта в измеряемом мессбауэровском спектре составляет 10 %, то необходимо накапливать спектр до 1010 импульсов в канал, а это потребует большого времени измерения. На практике обычно ограничиваются набором спектра до 107 импульсов. В этом случае ширина канала не должна превышать 0.15 Г. Следует отметить, что уменьшение ширины канала не приведет к улучшению качества, получаемой из спектра информации.

Из вышесказанного следует, что ограничение ширины канала снизу определяется статистикой. При прочих равных условиях число набранных в канале отсчетов пропорциональна ширине канала, поэтому очень малая ширина канала приведет к тому, что статистика будет плохой, а флуктуации от канала к каналу будут значительными.

Оба описанных в данной работе подхода могут применяться для дискретизации шкалы в любом виде спектрального анализа.